РАЗДЕЛ. IV. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

Если функция f (x) является полиномом (многочленом), то уравнение называ-

ется алгебраическим. Если степень этого полинома выше четвертой, то формул, записывающих в явном виде решение такого уравнения не существует. Еще хуже обстоит дело с уравнениями, не являющимися алгебраическими (такие уравнения называются трансцендентными). Точные решения таких уравнений удается найти лишь в некоторых частных случаях.

В связи с этим возникает задача об отыскании приближенного решения уравнения (30). Данная задача ставится одним из следующих способов.

нению с заданной точностью ε. Это означает, что должно выполняться нера-

близко корню (выполнено условие (31)), а значение функции при этом будет большой (условие (32) не удовлетворяется) (см. рис. 9.1.1,а). Возможна и противоположная ситуация (см. рис. 9.1.1,б). Ясно, что здесь играет роль крутизна

графика функции.

120

РИС. 9.1.1

Первая постановка задачи в большинстве случаев более естественна, чем вторая. Поэтому в дальнейшем мы будем иметь в виду первую постановку задачи.

Рассмотрим теперь некоторые методы приближенного решения уравне-

ний.

9.1.1.2. Графический метод

Если требуется отыскать корни уравнения (30) с небольшой точностью, то можно поступить следующим образом. Построить график функции y = f (x) и

найти точки пересечения его с осью x , которые дадут значения корней уравнения.

В том случае, когда график функции y = f (x) построить сразу не удается,

иногда делают иначе. Решаемое уравнение (30) преобразуют к виду

ϕ(x) = ψ(x)

так, чтобы графики функций y = ϕ(x) и y = ψ(x) были по возможности проще.

Тогда корни уравнения находятся как абсциссы точек пересечения этих двух графиков.

9.1.1.3. Отделение корней

Большинство приближенных методов не позволяет находить все корни уравнения сразу, они применяются к каждому корню в отдельности. Поэтому первая задача, возникающая при решении уравнения, состоит в том, чтобы узнать, сколько корней имеет уравнение, и для каждого из них (по крайней мере,

121

для тех, которые надо отыскать) найти интервал, на котором кроме этого корня нет других корней. Эта задача называется задачей отделения корней уравне-

ния.

Практически самый простой способ отделения корней – графический (см. п. 9.1.1.2). При этом, поскольку в дальнейшем значение корня предполагается уточнять, то графики можно строить достаточно схематично.

При решении задачи об отделении корней часто используется следующая теорема.

Если на отрезке [x1, x2 ] функция f (x) непрерывна и на концах его имеет значения разных знаков, то на этом отрезке имеется корень (возможно не один) уравнения f (x) = 0 . Если, кроме того, функция f (x) дифференцируема и f ′(x)

сохраняет знак на всем отрезке, то на этом отрезке имеется единственный корень.

9.1.1.4. Метод деления отрезка пополам

Пусть корень уравнения отделен отрезком [x1, x2 ]. Будем считать, что функция f (x) непрерывна на этом отрезке и значения функции на концах от-

резка имеют разные знаки ( f (x1) f (x2 ) < 0 ). Требуется сузить отрезок так, что-

бы корень содержался в новом суженном отрезке.

Самый простой способ для этого состоит в следующем. Найдем середину отрезка x3 = x1 +2 x2 и вычислим f (x3 ) . Если f (x1) f (x3 ) < 0 , то корень лежит

на отрезке [x1, x3 ] , а если f (x2 ) f (x3 ) < 0, то – на отрезке [x3 , x2 ]. Таким образом, мы вдвое уменьшили длину отрезка, отделяющего корень.

Найдя середину нового отрезка и определив знак функции в ней, мы уменьшим длину отрезка еще в два раза. Очевидно, продолжая эту процедуру многократно, можно сделать длину отрезка, заключающего корень, сколь угодно малой, то есть вычислить корень, удовлетворяющий условию (31) с любой степенью точности ε.

122

Описанный метод деления отрезка пополам (метод бисекции) доста-

точно трудоемок. Дальше мы рассмотрим методы, которые делают процесс приближения к корню более целенаправленным и менее трудоемким.

9.1.1.5. Метод хорд

Пусть выполняются следующие условия:

1)функция f (x) непрерывна на отрезке [a,b] ;

2)на концах отрезка функция принимает значения противоположных зна-

ков;

3) производные f ′(x) и f ′′(x) являются знакопостоянными функциями во всех точках отрезка [a,b] .

Последнее условие означает, что функция f (x) монотонна и график ее на всем отрезке либо выпуклый, либо вогнутый.

Из этих условий, в частности, вытекает, что на отрезке содержится единственный корень уравнения f (x) = 0 .

Суть метода хорд состоит в следующем.

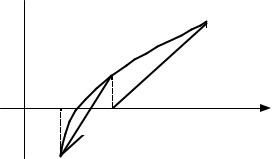
Корень уравнения – это абсцисса точки пересечения графика функции y = f (x) с осью x. Приближенное значение корня можно получить, заменив график функции на рассматриваемом отрезке [a,b] хордой, соединяющей его концы (рис. 9.1.2).

y

РИС. 9.1.2

Найдем это приближенное значение корня x0 . Хорда – это прямая линия,

проходящая через точки (a, f (a)) и (b, f (b)). Тогда ее уравнение имеет вид

123