
- •Множини
- •Відображення
- •1.3. Бінарні відношення на множині
- •2.1. Принцип математичної індукції Аксіома математичної індукції
- •Узагальнення другої форми принципу математичної індукції
- •2.2. Підстановки
- •Основні алгебраїчні структури
- •3.1. Означення комплексного числа
- •3.2. Дії над комплексними числами
- •3.3. Піднесення до степеня і добування кореня
- •4.1. Поліноми від однієї змінної
- •Г) Найбільший спільний дільник
- •Д) Найменше спільне кратне
- •4.3.Поліноми над числовими полями
- •4.4. Поліноми від багатьох змінних
- •Б) Симетричні поліноми
- •5.1. Поняття матриці
- •5.2. Дії над матрицями
- •6.1. Визначники малих порядків
- •6.2. Поняття визначника n-го порядку
- •6.3. Властивості визначника n-го порядку
- •6.4. Обчислення визначників n-го порядку
- •7.1. Загальні поняття
- •7.2. Способи розв’язування систем лінійних рівнянь
- •7.3. Матрична форма запису системи лінійних рівнянь
- •8.1. Поняття векторного простору, його розмірність і базис
- •8.3. Підпростори векторного простору
- •8.4. Лінійні перетворення у векторному просторі
- •8.5. Власні вектори і власні значення лінійного перетворення а) Інваріантні підпростори
- •Звідси із лінійної незалежності векторів e1, e2, …, en випливає:
- •9.1. Поняття евклідового простору
- •9.2. Ортонормований базис
- •9.3. Лінійні перетворення в евклідовому просторі
- •Властивості:
- •10.1. Лінійна функція (форма)
- •10.2. Поняття білінійної та квадратичної функції
- •10.3. Зведення квадратичної форми до суми квадратів
- •10.4. Закон інерції квадратичних форм
- •10.5. Класифікація квадратичних форм
- •10.6. Білінійні і квадратичні форми в евклідовому просторі
- •10.7. Зведення рівняння другого порядку до канонічного вигляду
- •Виконаємо лінійне перетворення
- •11.2. Зведення матриць до жорданової нормальної форми
- •Необхідна і достатня умова зведення матриць до діагонального вигляду
4.3.Поліноми над числовими полями
а)
Поліноми
над полем С

Теорема (про звідність полінома в полі С). Кожний поліном степеня вищого одиниці є звідним в полі С.
Доведення.
Якщо
f(x)
– поліном
степеня
 ,
то існує хоча б один корінь
,
то існує хоча б один корінь цьогополінома
і, за наслідком з теореми Безу,
цьогополінома
і, за наслідком з теореми Безу,
 ,
тобто
,
тобто
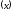 .
Оскільки
.
Оскільки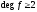 ,
то
,
то >0,
отже,
>0,
отже, звідний
в полі С.
▲
звідний
в полі С.
▲
Наслідок 1. Для того, щоб поліном був незвідним у полі С, необхідно
і достатньо, щоб його степінь дорівнював одиниці.
Наслідок 2. Кожний поліном над полем С єдиним способом
розкладається на лінійні множники в цьому полі:
 ,
де
,
де
 ,
, ,…,
,…, -
корені,
-
корені,
 –старший
коефіцієнт полінома
–старший
коефіцієнт полінома
 .
.
Якщо в розкладі існують кратні множники, то
 ,
,
де
 ,
, ,…,
,…, – різні корені полінома
– різні корені полінома ,
,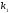 ,
, ,…,
,…, – відповідно їх кратності.
– відповідно їх кратності.
б) Поліноми над полем R
Теорема
(про
спряжений корінь полінома).
Якщо комплексне число

є
коренем полінома
 над
полем
R,
то
спряжене число
над
полем
R,
то
спряжене число

теж є коренем цього полінома.
Доведення.
Обчислимо
 і відокремимо дійсну та уявну частини:
і відокремимо дійсну та уявну частини:
 .
.
Оскільки
 корінь
корінь ,
то
,
то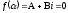 ,
звідки
,
звідки ,
, .
.
Обчислимо
тепер
 .
Оскільки
.
Оскільки ,
як дійсні числа, то
,
як дійсні числа, то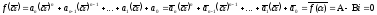 (оскільки
(оскільки
 ).
Отже,
).
Отже, ,
тобто
,
тобто –
корінь
–
корінь
 .
▲
.
▲
Обидва
корені
 та
та полінома
полінома
 мають, зрозуміло, однакову кратність.
мають, зрозуміло, однакову кратність.
Теорема (про звідність полінома в полі R). Кожний поліном над
полем R , степінь якого перевищує 2, є звідним у цьому полі.
Доведення.
Нехай
 коріньполінома
коріньполінома
 степеняn>2
над
полем R.
степеняn>2
над
полем R.
Якщо
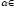 R,
то
R,
то
 ,
де
,
де
 і
і ,
,
тобто
 звідний
в полі R.
звідний
в полі R.
Якщо
 ,
то
,
то![]() теж
корінь
теж
корінь i
i
 ,
,
де
 і
і ,
причому
,
причому ,
тобто
,
тобто –
звідний
в R.
▲
–
звідний
в R.
▲
Із викладеного вище випливає наступне твердження:
кожний поліном f(x) над полем R має єдиний розклад на незвідні множники в цьому полі:
 .
.
в) Поліноми над полем Q
Основна відмінність поліномів над полем Q від поліномів над полями R та С полягає в тому, що над полем Q існують поліноми як завгодно високого степеня, незвідні в полі Q, тоді як в кільці R[x] звідним є довільний поліном степеня вищого 2, а в кільці С[x] – степеня вищого 1.
Ясно, що будь-яке алгебраїчне рівняння з раціональними коефіцієнтами множенням на спільний знаменник усіх коефіцієнтів можна звести до рівняння з цілими коефіцієнтами .
Терема Ейзенштейна (критерій незвідності).
Якщо
в поліномі
з цілими коефіцієнтами

 коефіцієнти
коефіцієнти
 ,
, діляться на деяке просте число
діляться на деяке просте число ,
причому
,
причому
 не ділиться на
не ділиться на ,
а старший коефіцієнт
,
а старший коефіцієнт
 не ділиться на
не ділиться на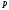 ,
то поліном
,
то поліном
 незвідний у поліQ
.
незвідний у поліQ
.
Доведення.
Досить
показати , що при заданих умовах
 не може бути добутком двохполіномів
ненульового степеня з цілими коефіцієнтами.
Припустимо супротивне, тобто, що
не може бути добутком двохполіномів
ненульового степеня з цілими коефіцієнтами.
Припустимо супротивне, тобто, що
 .
.
 .
.
Тут
r+s
= n.
Нехай
 .
.
Тоді








Оскільки
 ,
тобто
,
тобто ,
ділиться на
,
ділиться на ,
але не ділиться на
,
але не ділиться на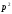 ,
то на
,
то на може ділитися лише одне з чисел:
може ділитися лише одне з чисел: або
або .
Нехай
.
Нехай ,
тоді
,
тоді .
З другої рівності випливає, що
.
З другої рівності випливає, що (бо
(бо за умовою, а
за умовою, а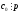 ).
Тоді з третьої рівності
).
Тоді з третьої рівності .
Так можна показати, що всі коефіцієнти
.
Так можна показати, що всі коефіцієнти діляться на
діляться на .
Але це неможливо, бо тоді й
.
Але це неможливо, бо тоді й ділилось б на
ділилось б на (із
останньої рівності), що суперечить умові
теореми.
(із
останньої рівності), що суперечить умові
теореми.

Отже,
 – незвідний в полі Q. ▲
– незвідний в полі Q. ▲
Таким чином, у кільці поліномів над полем Q є поліноми довільного степеня, незвідні в полі Q .
