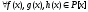4.1. Поліноми від однієї змінної

Поліномом (поліс – багато, номе – член) або многочленом від однієї змінної (невідомого) над цілісним кільцем R називається вираз вигляду

a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀,

де n – довільне ціле невід’ємне число, a_n, a_n-1, ..., a₁, a₀ – елементи цілісного кільця R, x, x²,…, x^n-1, xⁿ – деякі символи.

х^k називають k-м степенем змінної х, a_k – k-м коефіцієнтом полінома, a_kx^k – k-м членом полінома (k = 0, 1, ..., n), a₀ називають вільним членом.

Позначають поліноми від змінної х малими латинськими буквами: f(x), g(x), t(x), …, а множину всіх поліномів від х над цілісним кільцем R – R[x].

Відмінний від нуля член полінома f(x), степінь якого більший за степінь усіх інших ненульових членів цього полінома, називається старшим членом, його коефіцієнт – старшим коефіцієнтом, а його степінь – степенем полінома f(x). Степінь полінома f(x) позначають deg f (degree – степінь).

Форму запису полінома, впорядкованого за спаданням степеня x^k, називають канонічною. Елемент a₀ називають поліномом нульового степеня, а елемент θ – нуль-поліномом (позначають θ(х)).

Нехай задано два поліноми:

f(x) = a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ , a_iR, i = 0, 1, …, n,

g(x) = b_mx^m+b_m-1x^m-1+…+b₁x+b₀, b_jR, j = 0, 1, …, m.

Поліноми f(x) і g(x) називають рівними між собою, якщо канонічні форми цих поліномів співпадають, тобто рівними є степені обох поліномів і їх відповідні коефіцієнти.

Сумою поліномів f(x) і g(x) називається поліном

.

Добутком поліномів f(x) і g(x) називається поліном

де приi>n, 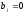приj>m.

Приклад

Теорема (про цілісне кільце поліномів). Множина R[x] усіх поліномів

над цілісним кільцем R утворює цілісне кільце відносно

операцій додавання і множення поліномів.

Доведення.

Дійсно, оскільки додавання і множення поліномів зводиться до виконання аналогічних операцій над їх коефіцієнтами, які є елементами деякого цілісного кільця R, то асоціативність і комутативність додавання і множення поліномів випливають із виконання відповідних властивостей в кільці R. Звідси ж випливає і дистрибутивність множення відносно додавання. Нульовий елемент в множині R[x] існує, це θ(х). Отже, R[x] – комутативне кільце. Залишилось показати відсутність дільників нуля. Якщо тоякщотоОтже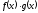має старший коефіцієнт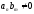(оскільки в R немає дільників нуля) і тому 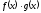не є нуль-поліномом, тобто R[x] – кільце цілісне, що й треба довести. ▲

4.2. Подільність поліномів

а) Ділення з остачею

Для розгляду теорії подільності поліномів від однієї змінної цілісне кільце R, якому належать усі коефіцієнти поліномів, потрібно замінити полем Р, для того, щоб для довільного елемента існував обернений елемент, або щоб разом із довільними двома елементами , поля Р до цього ж поля належала і їх частка . Цілісне кільце многочленів від однієї змінної з коефіцієнтами із поля Р позначають P[x].

В загальному випадку, два різні поліноми із P[x] не діляться один на одного. Однак, якщо операцію ділення поліномів в P[x] замінити більш загальною операцією ділення з остачею, то для P[x] можна побудувати теорію подільності, аналогічну теорії подільності цілих чисел.

Вважається, що поліном f(x)P[x] ділиться з остачею на поліном g(x)_≠θ(х)P[x], якщо в P[x] існують такі поліноми s(x) та r(x), що , причому абоr(x) = θ(х), або deg r<deg g.

Теорема (про ділення з остачею). Довільний поліном f(x) з кільця P[x]

однозначно ділиться з остачею на будь-який ненульовий

поліном з цього кільця.

Доведення.

а) Можливість ділення з остачею.

Нехай

Якщо f(x) = θ(х), то s(x) = θ(х) і r(x) = θ(х).

Якщо n = deg f < deg g = m, то s(x) = θ(х) і r(x) = f(x).

Нехай nm. Скористаємось методом індукції за n.

При n=0 отримаємо m=0, f(x)=a₀, g(x)=b_0(≠0), тому s(x)=, r(x)= θ(х). Ясно, що s(x)P[x], оскільки 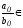P (саме тут потрібна заміна R на Р, здійснена на початку пункту).

Припустимо, що теорема вірна для всіх поліномів f(x) степеня, меншого за n, і доведемо її для поліномів степеня n.

Розглянемо поліном р(х) = f(x)- Cтарші члени обох поліномів у правій частині дорівнюють а_nхⁿ, а тому взаємно знищуються. Тоді deg p(x) < n і, за припущенням індукції, p(x) ділиться з остачею на g(x):

p(x)=g(x)·s₁(x)+r₁(x), де s₁(x), r₁(x) P[x], r₁(x)=0 або deg r₁<deg g.

Звідси

f(x) - = g(x)·s₁(x)+r₁(x),

тобто

f(x)=g(x)·s(x)+r(x),

де r(x)=r₁(x)P[x], s(x)=s₁(x),

причому r(x)= θ(х) або deg r<deg g.

Можливість ділення f(x) на g(x) з остачею доведена.

б) Покажемо єдиність частки s(x) і остачі r(x).

Припустимо, що можливі два варіанти ділення f(x) на g(x) з остачею:

f(x)=g(x)∙s(x)+r(x), deg r<deg g;

f(x)=g(x)∙s^*(x)+r^*(x), deg r^*<deg g.

Віднімемо записані рівності: g(x)[s(x) - s^*(x)] = r^*(x) - r(x).

За умовою g(x)θ(х). Якщо б r(x)r^*(x), то й s(x)s^*(x). Але тоді отримується суперечність, оскільки степінь правої частини менший степеня лівої частини. Отже, r(x) = r^*(x). Але тоді і s(x) = s^*(x). Таким чином, частка і остача визначаються однозначно. ▲

Наслідок. Кільце P[x] многочленів над полем Р є евклідовим.

На практиці ділення поліномів здійснюють способом „ділення кутом”, в основі якого лежить метод, використаний при доведенні теореми про ділення з остачею.

Оскільки частка s(x) і остача r(x) визначаються однозначно, то для їх знаходження можна користуватися і методом невизначених коефіцієнтів, який ґрунтується на прирівнюванні коефіцієнтів при однакових степенях x в лівій і правій частині рівності f(x)=g(x)∙s(x)+r(x), де s(x) шукають у вигляді полінома із невизначеними коефіцієнтами степеня n-m , а r(x) – степеня m-1.

Приклад

Поділити f(x) на g(x) і знайти s(x) та r(x):

f(x)=x⁴+2x³-x-3 , g(x)=x²-1.

1) Ділення кутом:

_x4+2x3 -x -3					x2-1
x4 –x2					x2+2x+1
_ 2x3 + x2
2x3 -2x
		_ x2 + x x2 -1
		x - 2

Отже, s(x)=x²+2x+1, r(x)= x-2.

2) Ділення методом невизначених коефіцієнтів:

x⁴+2x³-x-3=(x²–1)(A₂x²+A₁x+A₀)+(B₁x+B₀)

Отже, s(x)=x²+2x+1, r(x)= x-2.

б) Ділення многочлена на лінійний двочлен

Розглянемо важливий випадок ділення полінома f(x) на лінійний двочлен x-α. Скористаємось методом невизначених коефіцієнтів.

a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ = (x–α)(A_n-1x^n-1+A_n-2x^n-2+…+A₁x+A₀) + r.

Тут r = const, оскільки deg r(x)=m–1=1–1=0.

Прирівнявши коефіцієнти в обох частинах, отримаємо:

a_n=A_n-1 A_n-1=a_n,

a_n-1=A_n-2-αA_n-1 A_n-2=a_n-1+αA_n-1,

- - - - - - - - - - - - - - - - - - - - - - - - - - - -

a₁=A₀-αA₁ A₀=a₁+αA₁,

a₀=r-αA₀ r=a₀+αA₀.

Із отриманих формул видно, що поділити поліном на лінійний двочлен можна за певною схемою, яка називається схемою Горнера.

	an	an-1	an-2	an-3	…	a1	a0
α	an An-1	αAn-1+ +an-1 An-2	αAn-2+ +an-2 An-3	αAn-3+ +an-3 An-4		αA1+ +a1 A1	αA0+ +a0 A0

Приклад

Поділити поліном x⁵-2x³-3x²+2x-1 на x+1 за схемою Горнера.

	1	0	-3	1	-2	1
1	1	1	-2	-1	-3	-2
1	1	2	0	-1	-4
1	1	3	3	2
1	1	4	7
1	1	5
1	1

	1	0	-2	-3	2	-1
-1	1	-1	-1	-2	4	-5

Отже, s(x)=x⁴-x³-x²-2x+4, r= -5.

Теорема (Безу). Для довільного елемента α поля Р остача при

діленні полінома f(x)P[x] на x-α дорівнює f(α).

Доведення.

Згідно формули ділення з остачею, f(x)=(x-α)s(x)+r. Підставивши x=α, отримаємо f(α)=r, що й треба довести. ▲

За допомогою багаторазового ділення полінома f(x) на лінійний двочлен x-α з допомогою схеми Горнера можна дістати розклад полінома f(x) за степенями двочлена x-α, який часто використовується в алгебрі та математичному аналізі.

f(x)=(x-α)f₁(x)+r₀,

f₁(x)=(x-α)f₂(x)+r₁,

f₂(x)=(x-α)f₃(x)+r₂,

- - - - - - - - - - - - -

f_n-1(x)=(x-α)f_n(x)+r_n-1.

Ясно, що f_n(x) є поліномом нульового степеня. Позначимо f_n(x)=r_n. Виключивши послідовно всі f_i(x), i=1,2, …, n-1, отримаємо

f(x)=r_n(x-α)ⁿ+r_n-1(x-α)^n-1+…+r₁(x-α)+r₀.

Таким чином, отримаємо подання полінома f(x) як полінома від змінної y=x-α.

Приклад

Знайти розклад полінома f(x)= x⁵-2x³-3x²+2x-1 за степенями двочлена x+1.

	1	0	-2	-3	2	-1
-1	1	-1	-1	-2	4	-5
-1	1	-2	1	-3	7
-1	1	-3	4	-7
-1	1	-4	8
-1	1	-5
-1	1

f(x)=(x+1)⁵-5(x+1)⁴+8(x+1)³-7(x+1)²+7(x+1)-5.

в) Подільність поліномів

Розглянемо важливий випадок ділення поліномів “без остачі” (“націло”). В цьому випадку кажуть, що f(x) ділиться на g(x). Позначають: f(x)g(x).

Властивості подільності

1. 

2. 

3. 

4. (узагальнення 2, 3).

5. 

6. 

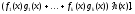
Всі ці властивості очевидні і випливають безпосередньо із властивостей подільності в довільному цілісному кільці.

Два поліноми із P[x] називаються асоційованими, якщо вони діляться один на одного. Такі поліноми можуть відрізнятися один від одного тільки сталим множником. Відношення “бути асоційованими” є відношенням еквівалентності.