8.5. Власні вектори і власні значення лінійного перетворення а) Інваріантні підпростори

Нехай V₁ – підпростір векторного простору V, A – деяке лінійне перетворення простору V. Образ Aх вектора х із V₁ не обов’язково належить V₁.

Розглянемо такі підпростори, вектори яких не виводяться із них перетворенням A.

Підпростір V₁ простору V називається інваріантним відносно лінійного перетворення A, якщо образ Aх кожного вектора х із V₁ належить V₁.

Приклади

1. Для лінійного перетворення A, яким є поворот навколо осі Оz звичайного тривимірного простору, інваріантними підпросторами будуть, наприклад, площина хОу і вісь Оz.

2. Для лінійного перетворення A, яким є ортогональне проектування того ж простору на площину хОу, інваріантними підпросторами будуть: площина хОу; всі площини, що проходять через вісь Оz; сама вісь Оz; всі прямі площини хОу, що проходять через початок координат.

3. Для тотожного і нульового перетворень, які діють в довільному просторі, інваріантними є всі його підпростори.

4. При довільному лінійному перетворенні в довільному просторі сам простір і його підпростір, що складається із одного нульового вектора, є інваріантними.

Теорема 1. Перетин і сума підпросторів, інваріантних відносно лінійного перетворення A, інваріантні відносно A.

Доведення.

а) Якщо підпростори V₁ і V₂ інваріантні відносно A і , тоі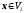, значить,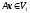і, тобто.

б) Якщо 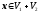, тоx=v₁+v₂, де ,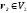. Тодіі, звідкиAх=+ ▲

Теорема 2. Якщо A – невироджене лінійне перетворення і V₁ – підпростір, інваріантний відносно A, то V₁ інваріантний і відносно A ^-1.

Доведення.

Нехай е₁, е₂, …, е_r – базис підпростору V₁. Тоді вектори

Aе₁, Aе₂, …, Aе_r, які із інваріантності V₁ теж належать V₁, теж лінійно незалежні і, значить, теж утворюють базис V₁, тобто довільний вектор можна через цей базис виразити:

Але тоді і

,

тобто

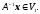
б) Власні вектори і власні значення лінійного перетворення

Розглянемо одновимірні інваріантні підпростори. Якщо V₁ – такий підпростір і , то і, і, значить,Aх=αх. Якщо у – будь-який інший вектор із V₁, то

у=αх і Aу= A(αх)=α(λх)=λ(αх)=λу.

Вектор називаєтьсявласним вектором лінійного перетворення A, якщо існує таке число λ, що Aх=λх. Число λ називається власним значенням перетворення A, яке відповідає власному вектору х.

Очевидно, що якщо V₁ – одновимірний інваріантний підпростір простору V, то кожний вектор із V₁ є власним вектором перетворення A, причому з одним і тим же власним значенням. Навпаки, якщо х – власний вектор перетворення A, то породжений ним інваріантний підпростір V₁ (що складається із всіх векторів вигляду αх) буде інваріантним відносно A.

Припустимо, що лінійне перетворення A має п лінійно незалежних власних векторів е₁, е₂, …, е_п із відповідними власними значеннями λ₁, λ₂, …, λ_п. Якщо власні вектори е₁, е₂, …, е_п прийняти за базисні, то із рівностей Aе₁=λ₁е₁, Aе₂=λ₂е₂, …, Aе_п=λ_пе_п матриця перетворення A матиме вигляд:

А=

(така матриця називається діагональною). Ясно, що правильне і зворотне: якщо матриця перетворення A в деякому базисі є діагональною, то всі вектори цього базису будуть власними векторами перетворення A.

Теорема 1. Власні вектори лінійного перетворення A, що

відповідають попарно різним власним значенням, лінійно

незалежні.

Доведення.

Доведення проведемо індукцією за кількістю власних векторів. Для одного вектора х це ясно, оскільки, за означенням власного вектора, він відмінний від нуля і, значить, із рівності αх=θ випливає, що α=0.

Нехай твердження теореми справедливе для k-1 векторів х₁, х₂, …, х_k-1. Припустимо, що k власних векторів х₁, х₂, …, х_k, які відповідають попарно різним власним значенням λ₁, λ₂, …, λ_k, є лінійно залежними:

α₁х₁+α₂х₂+…+α_kx_k=θ, ()

де не всі α_і (і=1, 2, …, п) рівні нулю. Застосувавши до обох частин рівності перетворення A, отримаємо

α₁ Aх₁+α₂ Aх₂+…+α_k Ax_k=α₁λ₁х₁+α₂λ₂х₂+…+α_kλ_kx_k=θ.

З другого боку, помноживши передостанню рівність на λ_k, матимемо

α₁λ₁х₁+α₂λ₂х₂+…+α_kλ_kx_k=θ.

Віднявши дві останні рівності, отримаємо

α₁(λ₁-λ_k)x₁+α₂(λ₂-λ_k)x₂+…+α_k-1(λ_k-1-λ_k)x_k-1=θ,

звідки із припущення лінійної незалежності х₁, х₂, …, х_k-1 випливає

α₁=α₂=…=α_k-1=0.

Тоді із рівності () матимемоα_kx_k=θ і α_k=0. Отже, припущення невірне. ▲

Розглянемо питання знаходження власних значень і власних векторів лінійного перетворення.

Припустимо, що х – власний вектор, а λ – відповідне йому власне значення лінійного перетворення A. Тоді Aх=λх. Виберемо в просторі V довільний базис е={e₁, e₂, …, e_n}, і нехай х=х₁е₁+х₂е₂+...+х_пе_п, а матриця лінійного перетворення A у вибраному базисі має вигляд

А

Тоді із пункту а) випливає:

Aх=(а₁₁х₁+а₁₂х₂+…+а_1пх_п)е₁+(а₂₁х₁+а₂₂х₂+…+а_2пх_п)е₂+…

+(а_п1х₁+а_п2х₂+…+а_ппх_п)е_п=

=λх=λ(х₁е₁+х₂е₂+...+х_пе_п)= λх₁е₁+ λх₂е₂+...+ λх_пе_п .