5.1. Поняття матриці

Матрицею порядку mn називають таблицю елементів із m рядків і n стовпчиків. Позначають:

А==, деі=1, 2, ..., m, j=1, 2, …, n,

або те саме в круглих дужках.

Матрицю порядку mn утворюють, наприклад, коефіцієнти при невідомих в системі m лінійних рівнянь з n невідомими:

Перші індекси біля елементів 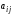є номерами рядків, а другі– стовпчиків. Елементи а_іі матриці A утворюють головну діагональ.

Дві матриці називають рівними, якщо співпадають їх елементи, що знаходяться на відповідних місцях. Матриця А', утворена із матриці А, в якій рядки і стовпчики помінялись місцями, називається транспонованою до матриці А:

А'.

Якщо всі елементи матриці рівні нулю, то матриця називається нульовою. Позначають θ.

Матрицю називають верхньою (нижньою) трикутною, якщо всі її елементи нижче (вище) головної діагоналі є рівними нулю.

Матрицю називають квадратною порядку n, якщо кількості рядків і стовпчиків співпадають і рівні n.

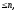Квадратна матриця [] порядкуn називається симетричною, якщо [a=a], і кососиметричною, якщо [= -],i j.

Матриця, у якої всі елементи, крім діагональних, рівні нулю, називається діагональною.

Якщо всі елементи діагональної матриці рівні між собою, то матрицю називають скалярною, якщо ж всі ці діагональні елементи рівні 1, то матрицю називають одиничною (позначають Е).

Матрицю називають ступінчастою (східчастою), якщо вона задовольняє такі умови:

1) якщо в і-му рядку перший ненульовий елемент знаходиться на k-му місці, то в наступному і+1-му рядку на перших k місцях знаходяться нулі;

2) якщо кожен елемент і-того рядка рівний нулю, то й кожен елемент наступного і+1-го рядка теж дорівнює нулю.

Приклад

,.

Елементарними перетвореннями матриці А називають такі операції:

1. переставляння двох рядків (стовпчиків) матриці А;

2. множення рядка (стовпчика) матриці А на деяке відмінне від нуля число с;

3. додавання до одного рядка (стовпчика) матриці А іншого її рядка (стовпчика), помноженого на деяке число с.

5.2. Дії над матрицями

Нехай А=і В=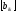– довільно вибраніпрямокутні(m, n)-матриці.

Сумою матриць А та В називають матрицю S =, де

,

Записують S=A+B.

Додавання матриць зводиться до додавання всіх пар їхніх відповідних елементів.

Приклад

+.

Ясно, що операція додавання матриць асоціативна і комутативна, оскільки вона зводиться до додавання елементів матриць. Крім того,

А [А+ θ = θ +А = А].

Добутком матриці А=[a_ik] на число λ називають матрицю B=[b_ik], де b_ik=λa_ik. Записують B=λA.

Множення матриці на число зводиться до множення всіх її елементів на число.

Приклад

3.

Множення матриці на число асоціативне і дистрибутивне як відносно додавання матриць, так і відносно додавання чисел:

R =;

;

.

Для означення поняття добутку матриць розглянемо питання про послідовне виконання лінійних перетворень змінних.

Нехай х₁, х₂, …, x_n – упорядкований набір змінних, значеннями яких можуть бути довільні числа,

B=_

довільно вибрана (s,n)-матриця з дійсними елементами. Утворимо такі вирази:

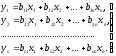
Ясно, що y₁,_, y₂, …, y_n теж є змінними, оскільки вони змінюються залежно від зміни x₁, x₂, …, x_n. Записаний перехід від системи змінних x₁, x₂, …, x_n до системи змінних y₁, y₂, …, y_n називається лінійним перетворенням змінних x₁, x₂, …, x_n у змінні y₁, y₂, …, y_n. Зрозуміло, що це лінійне перетворення повністю визначається своєю матрицею В.

Виконаємо тепер послідовно два лінійних перетворення. Нехай другим перетворенням буде лінійне перетворення змінних y₁, y₂, …, y_n в змінні z₁, z₂, …, z_n:

Матриця цього перетворення має вигляд : A=.

Виразимо тепер змінні z₁, z₂, …, z_m через змінні x₁, x₂, …, x_n, підставивши у другі співвідношення значення y₁, y₂, …, y_s із перших.

z₁=a₁₁(b₁₁x₁+b₁₂x₂+…+b_1nx_n)+a₁₂(b₂₁x₁+b₂₂x₂+…+b_2nx_n)+…+a_1s(b_s1x₁+b_s2x₂+…+b_snx_n)=

=(a₁₁b₁₁+a₁₂b₂₁+…+a_1sb_s1)x₁+(a₁₁b₁₂+a₁₂b₂₂+…+a_1sb_s2)x₂+…+(a₁₁b_1n+a₁₂b_2n+…+a_1sb_sn)x_n

z₂=a₂₁(b₁₁x₁+b₁₂x₂+…+b_1nx_n)+a₂₂(b₂₁x₁+b₂₂x₂+…+b_2nx_n)+…+a_2s(b_s1x₁+b_s2x₂+…+b_snx_n)=

=(a₂₁b₁₁+a₂₂b₂₁+…+a_2sb_s1)x₁+(a₂₁b₁₂+a₂₂b₂₂+…+a_2sb_s2)x₂+…+(a₂₁b_1n+a₂₂b_2n+…+a_2sb_sn)x_n

……………………………………………………………………………………….

z_m=a_m1(b₁₁x₁+b₁₂x_2+…+b_1nx_n)+a_m2(b₂₁x₁+b₂₂x₂+…+b_2nx_n)+…+a_ms(b_s1x₁+b_s2x₂+…+b_snx_n)=

=(a_m1b₁₁+a_m2b₂₁+…+a_msb_s1)x₁+(a_m1b₁₂+a_m2b₂₂+…+a_msb_s2)x₂+…

+(a_m1b_1n+a_m2b_2n+…+a_msb_sn)x_n.

Якщо подати отримані співвідношення у вигляді

z₁=c₁₁x₁+c₁₂x₂+…+c_1nx_n,

z₂=c₂₁x₁₊c₂₂x₂+…+c_2nx_n,

_{………………………………………..}

z_m=c_m1x₁+c_m2x₂+…+c_mnx_nm,

то c_ik=_ijb_jk, де i=1, 2, …, m; k=1, 2, …, n.

Як видно, результат послідовного виконання двох лінійних перетворень змінних теж є лінійним перетворенням змінних.

Матриця С результуючого лінійного перетворення має вигляд

С =,

де c_sk == a_і1b_1k+ a_i2b_2k +…+ a_isb_sk (i=1, 2, …, m; k=1, 2, …, n).

Матрицю С і називають добутком матриці А на матрицю В. Позначають С=АВ. Зрозуміло, що множити матриці можна тільки тоді, коли кожен рядок матриці А містить стільки елементів, скільки їх у кожному стовпчику матриці В.

Приклад

.

Очевидно, що множення матриць некомутативне. Операція множення матриць асоціативна і дистрибутивна відносно додавання:

(АВ)С=А(ВС);

(А+В)С=АС+ВС;

С(А+В)=АС+СВ.

Лекція 6. Визначники