7.2. Способи розв’язування систем лінійних рівнянь

а) Метод Гауса розв’язування систем лінійних рівнянь

Нехай задано довільну систему m лінійних рівнянь з п невідомими

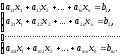
У цій системі хоча б один із коефіцієнтів біля невідомої відмінний від нуля, бо інакше система не мала бп невідомих. Якщо =0, але 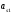≠0, то, переставивши перше та s-те рівняння, отримаємо еквівалентну систему, у першому рівнянні якої коефіцієнт при х₁ буде відмінним від нуля. Тому вважатимемо, що ≠0.

Запишемо розширену матрицю системи, відокремивши стовпчик вільних членів:

Застосовуючи елементарні перетворення рядків, зведемо цю матрицю до східчастого вигляду. Систему лінійних рівнянь, розширена матриця якої східчаста, також називають східчастою. Ясно, що східчаста система еквівалентна початковій системі. Перетворення системи лінійних рівнянь у східчасту систему називають зведенням системи лінійних рівнянь до східчастого вигляду. Позначимо східчасту матрицю, отриману з матриці , через.

Розглянемо такі можливі випадки:

1. У розширеній матриці є рядок, в якому першим ненульовим елементом є його останній елемент.

2. У матриці такого рядка немає.

В першому випадку в східчастій системі міститься рівняння вигляду деb≠0. Оскільки жодна система чисел не може задовольнити рівняння 0=b, де b≠0, то така східчаста система несумісна.

В другому випадку східчаста система містить r ненульових рядків і нехай перші ненульові елементи цих рядків знаходяться в стовпчиках з номерами k₁=1, k₂, k₃, …, k_r, де k₁<k₂<k₃<…<k_r<n. Всі рівняння системи вигляду 0·х₁+0·х₂+…+0·х_n=0 відкинемо. Невідомі , з яких починається перше, друге, …,r-те рівняння системи, називають головними, а всі інші (якщо вони є) – вільними.

Якщо вільних невідомих немає, тоді r=n, звідки k₁=1, k₂=2, k₃=3, …, k_r=n, і система матиме трикутний вигляд:

де

Із останнього рівняння знаходимо х_п, а потім, підставивши його в попереднє рівняння, знаходимо х_п-1, і т.д., в результаті отримаємо єдині значення невідомих, які і становлять єдиний розв’язок системи. Отже, при відсутності вільних невідомих східчаста система лінійних рівнянь сумісна і визначена.

Якщо вільні невідомі є, то система має вигляд:

де 1<k₂<k₃<…<k_r<n.

Позначимо символом В_і суму всіх тих членів і-го рівняння системи, які містять вільні невідомі. Перенесемо члени з вільними невідомими в праві частини рівнянь і отримаємо:

де

Надавши вільним невідомим довільно вибраних числових значень, отримаємо попередній випадок системи без вільних невідомих, який дає єдині значення головних невідомих Сукупність знайдених значень головних невідомих і вибраних нами значень вільних невідомих, ясно, є цілком визначеним розв’язком східчастої системи, який відповідає вибраним значенням вільних невідомих. Оскільки значення вільних невідомих можна вибрати довільно, то множина різних наборів, а, значить, множина розв’язків східчастої системи є нескінченною. Таким чином, при наявності вільних невідомих східчаста система лінійних рівнянь сумісна, але невизначена.

Іншими словами, доведено теореми:

Теорема 1. Система лінійних рівнянь сумісна тоді і тільки тоді,

коли вона зводиться до ступінчастої системи, в якій

немає рівнянь вигляду 0=b, де b≠0.

Теорема 2. Система лінійних рівнянь є визначеною тоді і тільки

тоді, коли вона зводиться до ступінчастої системи, в

якій число рівнянь r дорівнює числу невідомих n.

Наслідок 1. Система лінійних рівнянь з п невідомими є визначеною

тоді і тільки тоді, коли вона зводиться до ступінчастої

системи, в якій

Наслідок 2. Сумісна система m лінійних рівнянь з п невідомими при

m<n є невизначеною.

Випадок однорідної системи

Лінійне рівняння називається однорідним, якщо його вільний член b дорівнює нулю. Система лінійних рівнянь називається однорідною, або системою лінійних однорідних рівнянь, якщо всі її вільні члени рівні нулю:

Однорідна система завжди сумісна, бо вона має нульовий розв’язок (0, 0, …, 0). Це видно із теореми 1, оскільки із того, що всі вільні члени рівні нулю, випливає відсутність у відповідній східчастій системі рівнянь вигляду 0=b, де b≠0.

Якщо однорідна система зводиться до східчастої, в якій кількість рівнянь r дорівнює кількості невідомих п, то, згідно теореми 2, вона має єдиний розв’язок – нульовий. Якщо ж однорідна система зводиться до східчастої, в якій кількість рівнянь r менша, ніж кількість невідомих п, то множина розв’язків такої системи нескінченна, а, значить, вона має і ненульові розв’язки. Згідно наслідку 2 така система невизначена.

Нехай 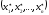=f₁ – деякий ненульовий розв’язок однорідної системи. Тоді cf₁=– теж розв’язок цієї системи. Якщо ж f₂= – якийсь інший ненульовий розв’язок цієї системи, то при довільних c₁ і c₂ лінійна комбінація записаних розв’язків теж буде розв’язком системи, оскільки якщо

і (і=1, 2, …, п),

то і

Таким чином, довільна лінійна комбінація розв’язків однорідної системи теж буде її розв’язком.

Важливими є такі лінійно незалежні розв’язки однорідної системи, через які лінійно виражаються всі решта її розв’язки.

Лінійно незалежна система розв’язків системи лінійних однорідних рівнянь називається фундаментальною, якщо кожний розв’язок однорідної системи є лінійною комбінацією цієї лінійно незалежної системи.

Ясно, що якщо кількість рівнянь r в східчастому вигляді однорідної системи є меншою кількості невідомих п, то така система рівнянь володіє фундаментальною системою розв’язків (ФСР). Очевидно також і те, що для отримання ФСР можна надавати n-r вільним невідомим довільних значень і так відшукати скільки завгодно різних ФСР, кожна з яких складалася б із n-r лінійно незалежних розв’язків.

Приклади

1. Розв’язати систему

Зведемо розширену матрицю цієї системи до східчастого вигляду.

Тут перетворення (1) включає: а) до 2-го рядка додано 1-й, помножений на (-2); б) до 3-го і 4-го рядків додано 1-й, помножений на (-3);

перетворення (2) включає: а) до помноженого на 5 3-го рядка додано помножений на (-8) 2-й рядок; б) від 4-го рядка віднято 2-й рядок.

Після вилучення рівняння вигляду 0=0 задана система лінійних рівнянь звелася до наступної східчастої системи:

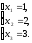
Ця система, а, значить, і задана система мають єдиний розв’язок.

2. Розв’язати систему

Зведемо розширену матрицю цієї системи до східчастого вигляду:

.

Ця система несумісна, оскільки містить рівняння 0=14.

3. Розв’язати систему

Зведемо розширену матрицю цієї системи до східчастого вигляду:

Отримано східчасту систему:

звідки, позначивши х₃ та х₄ вільними змінними, матимемо:

Це і є загальний розв’язок даної системи.

Частинні розв’язки: (1,-2,1,0), (та інші.

Викладений метод розв’язування систем лінійних рівнянь називається методом Гауса, або методом послідовного виключення невідомих.

3. Розв’язати однорідну систему і знайти її фундаментальну систему розв’язків

Отримаємо систему:

Загальний розв’язок:

–вільні невідомі.

Фундаментальну систему отримаємо, якщо вільним невідомим х₃, х₅ надамо значень 1,0 і 0,1 відповідно (визначник матриці відмінний від нуля). Отримаємо:

	x1 x2 x3 x4 x5
f1	1 –2 1 0 0
f2	15 –12 0 1 1

Розв’язки f₁ та f₂ і утворюють ФСР. Тоді ще один вигляд загального розв’язку системи: f=c₁f₁+c₂f₂, де c₁, c₂ – довільні числа.

б) Метод Крамера розв’язування систем лінійних рівнянь

Розглянемо систему п лінійних рівнянь з п невідомими, визначник d якої відмінний від нуля. Доведемо, що така система сумісна і визначена, і знайдемо формули для знаходження її єдиного розв’язку.

Припустимо, що наша система сумісна. Нехай – деякий її розв’язок. Тоді виконуються рівності:

Помножимо першу з рівностей на алгебраїчне доповнення А_1j елемента a_1j у визначнику системи, другу – на алгебраїчне доповнення A_2j і т. д., нарешті, останню з рівностей – на A_nj ( j=1, 2, .., n ), потім всі отримані рівності додамо. В результаті дістанемо таку рівність:

В записаній рівності всі коефіцієнти біля дорівнюють визначнику матриці системи (теорема 6.1), а всі інші коефіцієнти рівні нулю (теорема 6.2). Вираз у правій частині є розкладом визначника

за елементами j-го стовпчика, тобто є визначником d_j, який утворено з визначника d заданої системи рівнянь заміною його j-го стовпчика стовпчиком вільних членів. Тому отримана вище рівність запишеться так: (j=1, 2, …, n).

Звідси, оскільки d≠0 за умовою, отримаємо

Отже, якщо задана система п лінійних рівнянь з п невідомими сумісна, то вона має єдиний розв’язок

.

Таким чином, задана система або має єдиний розв’язок , або зовсім не має розв’язків. Тому для з’ясування питання про сумісність системи досить тільки з’ясувати, чи задовольняє система чиселзадану систему рівнянь. Для перевірки підставимо числав праву частинуі-го рівняння (і=1, 2, …, п).

(оскільки ).

Отже, множина чисел є розв’язком кожногоі-го рівняння (і=1, 2, …, п) системи, а, значить, і самої системи.

Таким чином, доведено теорему:

Якщо визначник d системи n лінійних рівнянь з n невідомими відмінний від нуля, то система має єдиний розв’язок: , де – визначник, отриманий із визначника d заміною його і-го стовпчика стовпчиком вільних членів системи.

Отримані формули розв’язку називають формулами Крамера, а саму теорему – правилом Крамера.

Наслідок. Система n лінійних однорідних рівнянь з п невідомими тоді і тільки тоді має розв’язки, відмінні від нульового, коли визначник цієї системи дорівнює нулю.

Доведення.

Якби визначник однорідної системи лінійних рівнянь був відмінним від нуля, то ця система мала б єдиний розв’язок (нульовий), що суперечить умові.

Навпаки, якщо визначник системи дорівнює нулю, то східчаста матриця цієї системи п рівнянь з п невідомими має хоча б один нульовий рядок, а, значить, кількість рівнянь у відповідній східчастій системі менша за число невідомих, звідки випливає існування вільних невідомих і, отже, нескінченної кількості розв’язків, в тому числі і відмінних від нульового. ▲

Правило Крамера пов’язане з громіздкими обчисленнями, але в тих випадках, коли воно застосовне, є можливість виразити всі компоненти розв’язку системи рівнянь через її коефіцієнти і вільні члени.

Приклад

Розв’язати систему рівнянь

Оскільки d0, то застосуємо правило Крамера:

Отже,

Розв’язок: (-1;0;1;2).

в) Матричний метод розв’язування систем лінійних рівнянь

Матриця А^-1 називається оберненою для квадратної матриці А, якщо АА^-1=А^-1А=Е. Тут Е – одинична матриця.

Виберемо довільну матрицю А п-го порядку:

А

Утворимо матрицю А*, елементами якої є алгебраїчні доповнення A_ij до відповідних елементів а_ij матриці, транспонованої до матриці А:

А*=

Матрицю А* називають взаємною (приєднаною) для матриці А. За правилом множення матриць отримаємо:

АА*= А*А==|А|*Е.

Матриця називається невиродженою, якщо її визначник не дорівнює нулю, і виродженою, якщо дорівнює нулю.

Відомо, що визначник добутку квадратних матриць дорівнює добутку визначників цих матриць, тому із останнього виразу випливає наступний висновок.

Теорема 1. Якщо матриця А невироджена, то взаємна їй матриця

А^* теж буде невиродженою, причому |А*|= |А|^n-1.

Доведення.

Дійсно, |А|·|А*|=|А|ⁿ, звідки при |А|≠0 і випливає сформульоване твердження. Тому із АА^-1=Е випливає |А|·|А^-1|=|E|=1. Це означає, що обернена матриця А^-1 існує тільки для невиродженої матриці А, бо в іншому випадку не буде виконуватись остання рівність. ▲

Теорема 2. Для довільної невиродженої матриці А існує тільки одна

обернена матриця А^-1.

Доведення.

Якби існувала ще одна матриця А₁, обернена до А, тобто така, що

АА₁=А₁А=Е, то А₁АА^-1=(А₁А)А^-1=ЕА^-1=А^-1, А₁АА^-1=А1(АА^-1)=А₁Е=А₁,

звідки А₁=А^-1. ▲

Із АА*= А*А=|А|ⁿ Е випливає А·|А|^-n ∙А*=Е, тобто А^-1=|А|^-n ∙А*.

Загальний вигляд оберненої матриці до А:

А^-1==|А|^-1 ∙ А*.

Якщо матриця А невироджена, то кожне з рівнянь АХ=В та УА=В має розв’язки: Х=А^-1В, У=ВА^-1.

Приклади

1. Знайти матрицю, обернену до матриці А=

Отже, обернена А^-1 існує:

А₁₁=5, А₁₂=10, А₁₃=0,

А₂₁=4, А₂₂=12, А₂₃=1,

А₃₁=-1, А₃₂=-3, А₃₃=1.

А^-1 =

2. Розв’язати рівняння АХ=В і УА=В, якщо А=, В=.

Матриця А^-1 невироджена і рівна А^-1= Тому

Х=А^-1В==.

У=ВА^-1=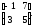=.