10.4. Закон інерції квадратичних форм

При зведенні квадратичної форми А(x, x) до суми квадратів різними способами можна отримати різні канонічні коефіцієнти. Однак має місце наступне твердження:

Теорема (закон інерції квадратичних форм).

Кількість доданків з додатніми (від’ємними) канонічними коефіцієнтами в канонічному вигляді квадратичної форми не залежить від способу зведення форми до цього вигляду.

Доведення.

Припустимо супротивне, тобто що в базисі e=(e₁,e₂,…,e_n) квадратична форма А(x, x) має вигляд

А(x, x) , (*)

де – координати вектораx в цьому базисі,

а в іншому базисі e' = (e₁^', e₂^',…, e_n^') форма А(x, x) має вигляд

А(x, x) , (**)

де 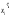– координати вектораx в новому базисі. Припустимо, що, наприклад, p>k.

Розглянемо в просторі V підпростір , породжений векторамиe₁, e₂, …, e_n, і підпростір , породжений векторами. Оскільки сума їх розмірностейp+(n-k) більша за n, то їх перетин має ненульову розмірність, тобто існує вектор , який належить. Цей вектор можна подати як у вигляді

,

так і у вигляді

.

Для вектора х за формулою (*) А(x, x) , оскільки хоча б одне із . В той же час для векторах за формулою (**) А(x, x) .

Ми отримали протиріччя, із якого випливає, що pk. Аналогічно доводиться: неможливість нерівності p<k. Значить, p=k. Так само доводиться, що q=m.

Ясно, що сума p+ q дорівнює рангу r квадратичної форми.

Приклад

Дослідити знаковизначеність квадратичної форми

.

Запишемо матрицю цієї форми

А.

Обчислимо кутові мінори:

,

отже, задана квадратична форма додатньо визначена.

10.5. Класифікація квадратичних форм

Квадратична форма називається додатно (від’ємно) визначеною, якщо для А(x,x)>0 (А(x,x)<0) і додатно (від’ємно) напіввизначеною (квазівизначеною), якщо А(x,x) (А(x,x) ).

Приклад

Скалярний квадрат А(x,x)=(х,х) є додатно визначеною квадратичною формою.

Ясно, що додатно визначена квадратична форма зводиться до суми квадратів з додатними канонічними коефіцієнтами, додатно напіввизначена форма – з невід’ємними коефіцієнтами (деякі з них можуть дорівнювати нулю).

Теорема (критерій Сильвестра).

Для того, щоб квадратична форма А(x, x) була додатно визначеною, необхідно і достатньо, щоб всі кутові мінори матриці А=[a_ij] були додатними.

Для того ж, щоб квадратична форма була від’ємно визначеною, необхідно і достатньо, щоб знаки кутових мінорів чергувались, причому .

Доведення.

а) Необхідність. Покажемо спочатку, що із умови знако-визначеності квадратичної форми А(x, x) випливає ,і=1, 2, ..., n.

Переконаємось, що припущення веде до протиріччя – при цьому припущенні існує ненульовий векторх, для якого А(x, x)=0, що суперечить знаковизначеності форми.

Нехай . Розглянемо наступну квадратну однорідну систему лінійних рівнянь:

.

Оскільки – визначник цієї системи, і=0, то записана система рівнянь має ненульові розв’язки (не всіх рівні нулю). Помноживши перше із рівнянь системи на , друге на, ..., останнє наі додавши отримані співвідношення, отримаємо рівність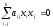, ліва частина якої є значенням квадратичної формиА(x, x) для ненульового вектора х з координатами . Це значення рівне нулю, що суперечить знаковизначеності форми. Отже,,і=1, 2, ..., n.

Застосуємо метод Якобі зведення форми А(x,x) до суми квадратів. Якщо А(x,x) – додатно визначена форма, то із формул для знаходження канонічних коефіцієнтів отримаємо 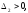...,. Якщо жА(x, x) – від’ємно визначена форма, то з тих же формул випливає, що знаки кутових мінорів чергуються, причому.

б) Достатність. Згідно умови теореми всі ,і=1, 2, ..., n, тому, скориставшись методом Якобі, отримаємо у першому випадку додатно, а в другому – від’ємно визначену квадратичну форму.