3.1. Означення комплексного числа

В історії розвитку математичної науки час від часу виникали проблеми, пов’язані з необхідністю поповнення числового запасу, яка грунтувалася на відсутності в попередніх множинах розв’язків окремих типів рівнянь. Так, у випадку розширення множини Z цілих чисел множиною Q раціональних чисел це були, наприклад, рівняння ax=b, де а,bZ, у випадку розширення множини Q множиною R дійсних чисел – рівняння axⁿ=b, де a,bQ, nN. Наступний тип рівнянь, наприклад, х²+1=0, став причиною необхідності розширення множини дійсних чисел, оскільки в ній коренів цього рівняння не існує. Розглянемо спосіб розв’язання останньої проблеми.

В ролі елементів нової множини чисел виберемо точки площини, які позначатимемо буквами α, β, γ, … . Вибравши на площині прямокутну систему координат, записуватимемо точку α з абсцисою а і ординатою b через α = (a,b).

Сумою α+β точок α = (a,b) і β = (c,d) назвемо точку з абсцисою а+с і ординатою b+d, тобто

α+β = (a,b)+(c,d) = (a+c,b+d).

Добутком α·β цих же точок назвемо точку з абсцисою ас-bd і ординатою ad+dc, тобто

α·β = (a,b)·(c,d) = (ac-bd, ad+bc).

Пряма перевірка аксіом поля підтверджує, що множина точок площини із вибраними таким чином операціями додавання і множення утворює поле. Це числове поле (в якому числа зображаються точками площини) названо полем комплексних чисел. Якщо точці (а,0) осі абсцис поставити у відповідність дійсне число а, то отримається взаємно однозначна відповідність (ізоморфізм) між точками осі абсцис і множиною дійсних чисел, причому операції додавання і множення точок осі абсцис і дійсних чисел є аналогічними:

(а,0)+(b,0) = (a+b,0), (а,0)·(b,0) = (ab,0).

Тому не розрізнятимемо точку (а,0) та дійсне число а і вважатимемо (а,0) = а. Отже, поле комплексних чисел містить підмножину точок осі абсцис, ізоморфну полю дійсних чисел, тобто є його розширенням.

Покажемо, що це розширення містить корені рівняння х²+1=0, тобто в ньому є елемент, квадрат якого рівний -1. Розглянемо точку (0,1), яка лежить на осі ординат на відстані 1 вгору від початку координат, і знайдемо її квадрат: (0,1)·(0,1) = (-1,0) = -1. Позначають точку (0,1) буквою і. Отже, і² = -1.

Для побудованих комплексних чисел отримаємо звичайний запис:

(a,b) = (a,0)+(0,b) = (a,0)+b·(0,1) = a+bi.

Ця форма запису комплексного числа називається алгебраїчною. В записі комплексного числа число а називають його дійсною частиною (позначають Re α), а число bi – його уявною частиною (позначають Im α).

Площина, точки якої ототожнені з комплексними числами, названа комплексною площиною, вісь абсцис – дійсною віссю, вісь ординат – уявною віссю.

Число 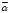= a-bi, яке відрізняється від = a+bi тільки знаком при уявній частині, називається числом, спряженим з . Геометрично спряжені числа є точками, розміщеними симетрично відносно дійсної осі.

-bi

a

bi

3.2. Дії над комплексними числами

1. (a+bi) + (c+di) = (a+c) + (b+d)i.

2. (a+bi) – (c+di) = (a – c) + (b – d)i.

3. (a+bi)(c+di) = (ac – bd) + (ad+ bc)i.

4. = =+i.

5. = .

6. = +.

7. = -.

8. = ·.

9. = .

Доведення всіх формул здійснюється безпосередньо.

+

α = a+bi,

β = c+di.

0

с

а

d

b

Із малюнка видно, що додавання комплексних чисел геометрично здійснюється за правилом паралелограма (аналогічно віднімання – за правилом трикутника).

Оскільки комплексні числа розміщені не на одній прямій, то їх не можна впорядкувати з допомогою понять “більше” і “менше”, тому поле комплексних чисел невпорядковане.

Тригонометрична форма комплексного числа

Положення точки на комплексній площині може бути задане як декартовими координатами а,b (α=a+bi), так і її полярними координатами: відстанню r від початку координат до точки і кутом  між додатнім напрямом осі абсцис і напрямом із початку координат на цю точку.

0



b

α

r

a

Число r називають модулем числа α (позначається ), а кут – аргументом числа α (позначається arg). Зв’язок між декартовими та полярними координатами: a = rcos, b = rsin. Звідси r = . Тому

запис числа α в полярних координатах є наступним:

α = a+bi = rcos+(rsin)i, тобто

α = r(cos+isin).

Ця форма запису комплексного числа називається тригонометричною.

Приклад

Число α = 1 + і в тригонометричній формі виглядає так:

α = (cos+isin).

Знайдемо добуток двох комплексних чисел α = r(cos+isin) та β = .

Таким чином,

, ,

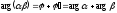тобто модуль добутку комплексних чисел дорівнює добутку модулів співмножників, а аргумент добутку комплексних чисел дорівнює сумі аргументів співмножників.

Ці правила поширюються на довільну кількість співмножників.

Аналогічні правила мають місце і для частки. Нехай β ≠ 0.

звідки випливає, що

модуль частки двох комплексних чисел дорівнює частці модулів діленого і дільника, а аргумент частки дорівнює різниці аргументів діленого і дільника.

Із того, що 1=1+і∙0=cos0+isin0, і при α=r(cos+isin)≠0 отримаємо

α^-1=r^-1[cos(-)+isin(-)].