Г) Найбільший спільний дільник

Спільний дільник поліномів f(x) та g(x), який ділиться на кожний інший їх спільний дільник, називається найбільшим спільним дільником (НСД) цих поліномів і позначається (f,g). НСД поліномів визначається однозначно з точністю до сталого множника (оскільки, якщо d(x) – НСД , то й c·d(x), де сР, теж НСД).

Поліноми f(x) та g(x) називаються взаємно простими, якщо кожний їхній спільний дільник є ненульовою константою, тобто (f,g)=1.

Розглянемо спосіб знаходження НСД (алгоритм Евкліда).

Нехай задано поліноми f(x) та g(x), причому . Виконаємо послідовне ділення з остачею:

Тут оскільки послідовність степенівполіномів g(x), r₁(x), r₂(x),... є монотонно спадною. Степінь r₁(x) не вищий за m-1, де m=deg g, тому кількість кроків в алгоритмі не перевищує m.

Оскільки (f,g)=(g,r₁)=(r₁,r₂)=(r₂,r₃)=…=(r_n-1,r_n)=(r_n,θ)=r_n, то остання відмінна від нуля остача r_n(x) в алгоритмі Евкліда і є НСД поліномів f(x) і g(x).

Приклад

З допомогою алгоритму Евкліда знайти НСД поліномів

f(x)=x³+x²+x+1, g(x)= x³+x²-x-1.

x³+x²+x+1=(x³+x²-x-1)·1+(2x+2),

x³+x²-x-1=(2x+2)·(x²-1)+0.

Отже, (f,g)=x+1.

НСД довільної кількості поліномів, зокрема, f₁(x), f₂(x),…, f_n(x) визначають послідовними кроками:

d₁(x)=(f₁,f₂), d₂(x)=(d₁,f₃), d₃(x)=(d₂,f₄), …, d_n-1(x)=(d_n-2,f_n).

d_n-1(x) і є НСД поліномів f₁(x), f₂(x),…, f_n(x).

Якщо хоча б два поліноми із системи f₁(x), f₂(x),…, f_n(x) є взаємно простими, то НСД усіх цих поліномів дорівнює одиниці.

Піднімаючись вгору рівностями алгоритму Евкліда і позначивши d(x)=r_n(x), отримаємо вираз

d(x)=f(x)·u(x)+g(x)·v(x),

тобто P[x], такі що НСД (f,g) двох поліномів виражається через ці поліноми f(x) і g(x).

Д) Найменше спільне кратне

Найменшим спільним кратним (НСК) поліномів f(x) та g(x) називається спільне кратне цих поліномів, на яке ділиться довільне інше їх спільне кратне. Позначається [f, g].

Теорема (про НСК поліномів). Для довільних ненульових поліномів

f(x), g(x) НСК існує і визначається з точністю до сталого

множника.

Доведення.

Для доведення розглянемо поліном 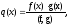який є спільним кратним f(x) та g(x), оскільки ділиться на кожний з них. Нехай s(x) – довільне інше спільне кратне поліномів f(x) і g(x). Тод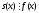і і, звідкиs(x)=s₁(x)·f(x), а також тобто

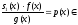P[x].

Замінимо f(x)=(f,g)·f₁(x), g(x)=(f,g)·g₁(x), де (f₁,g₁)=1. Звідси

.

Із (f₁,g₁)=1 випливає, що 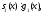тобтоs₁(x)=g₁(x)·t(x), звідки Отже,,

тобто q(x) – найменше спільне кратне поліномів f(x) та g(x).

Якщо q₁(x) – деяке інше НСК, то 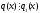і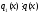, тобтоq_l(x) та q(x) відрізняються тільки сталим множником. ▲

е) Звідність поліномів

Поліном f(х)Р[x] називається незвідним у полі Р, якщо він не є константою і не має дільників, відмінних від константи та асоційованих з ним многочленів. В іншому випадку поліном називають звідним. Поняття звідності є відносним і залежить від поля Р, над яким поліном розглядається.

Приклад

Поліном f(х)= x-3 незвідний у полі Q, але звідний у полі R:

f(x)= (x-)(x+).

Поліном f(x)= x+3 незвідний в полях Q, R, але звідний у полі С:

f(x)= (x-i)(x+i).

Якщо поліном f(х) незвідний у полі Р, то він вже є добутком незвідних в даному полі поліномів (один співмножник). Якщо поліном f(х) звідний у полі Р, то, розклавши його і всі його співмножники в добуток незвідних поліномів у даному полі, отримаємо зображення полінома, яке називають розкладом полінома f(х) на незвідні множники:

f(x) = р(х)·р(х) ·...·р(х),

де р(х) – незвідні в полі Р, і=1, 2, ..., l.

Звідси випливає ще один запис полінома f(x):

f(x) = [p(x)][p(x)]…[p(x)],

де р(х) – попарно різні (неасоційовані) поліноми, незвідні в полі Р.

Таке зображення називають канонічним розкладом полінома f(x) в полі Р.

є) Корені поліномів

Коренем полінома f(x)Р[x] називається елемент будь-якого розширення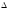поля Р такий, щоf() = 0.

Теорема (про корінь полінома). Елемент Р є коренем полінома

f(x)Р[x] тоді і тільки тоді, коли поліном f(х) ділиться на х-α.

Доведення.

За теоремою Безу f(х)=(х-)f(x)+ f(). Звідси, f(х) ділиться на х- тоді і тільки тоді, коли f()=0, тобто коли – коріньf(х).▲

Інше (рівносильне при =Р) означення кореня.

Коренем полінома f(х)Р[x] називається такий елемент αР, для якого f(х)х-α.

Елемент αР називається k-кратним коренем полінома f(х)Р[x], якщо f(х) ділиться на (х-α), але не ділиться на (х-α).

Кількість усіх можливих коренів полінома f(х) над полем Р не перевищує степеня полінома.

На питання, чи кожен поліном ненульового степеня має хоча б один корінь, відповідь дає теорема Кронекера:

Якщо f(х) – довільний поліном ненульового степеня над полем Р, то існує розширення К поля Р, в якому f(х) має корінь.

Наслідком із цього твердження є наступне:

Для довільного полінома f(х)P[x] ненульового степеня існує таке розширення L поля Р, в якому f(х) розкладається на лінійні множники. Тобто, якщо ,,...,L є коренямиполінома f(х), то

f(x)=a(x-)(x-)…(x-),

де а_n – старший коефіцієнт f(х).

Поле L, в якому поліном f(x) розкладається на лінійні множники, називається полем розкладу цього полінома.

Приклад

Знайти поле розкладу для полінома f(x) = x⁴ - 9.

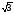x-9 = (x-3)(x+3)=(x -)(x+)(x-i)(x+i).

Оскільки корені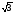 -,,-і, і належать полю С, то поле С і є полем розкладу полінома f(x) = x-9.

Поле Р називається алгебраїчно замкнутим, якщо воно є полем розкладу для довільного полінома f(х)P[x] ненульового степеня, тобто якщо всі корені будь-якого полінома f(х)P[x] належить цьому ж полю.

Поле С комплексних чисел є прикладом алгебраїчно замкнутого поля.

Теорема Вієта. Якщо 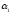,,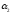...,– корені полінома

f(х) = ах+ах+...+ах+аP[x], то

++...+= -,

+,

………………………………………………………….

.

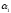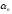Доведення цього твердження здійснюється прирівнюванням коефіцієнтів при однакових степенях х в обох частинах.

Теорема (про кратність похідної полінома). Якщо незвідний в полі Р

характеристики 0 поліном q(x) є множником кратності

k>1 полінома f(x), то він є множником кратності k-1 для

похідної f(х).

Доведення.

Якщо q(x) – множник кратності k полінома f(х), то

f(x)=[q(x)]·(x), де (х) не ділиться на q(x).

Тоді

f(x)=k[q(x)]·q(x)·(x)=[q(x)]^k-1·[k·q(x)·(x)].

Видно, що .

Залишилось показати, що вираз в других квадратних дужках не ділиться на q(x). Перший доданок на q(x) не ділиться (оскільки q'(x) має нижчий степінь, ніж q(x), а φ(x) не ділиться на q(x) за умовою), а другий доданок на q(x) ділиться, тому сума цих доданків на q(x) не ділиться. Отже, f'(x)[q(x)]^k-1, тобто q(x) – множник f'(x) кратності k-1.▲