
- •Множини
- •Відображення
- •1.3. Бінарні відношення на множині
- •2.1. Принцип математичної індукції Аксіома математичної індукції
- •Узагальнення другої форми принципу математичної індукції
- •2.2. Підстановки
- •Основні алгебраїчні структури
- •3.1. Означення комплексного числа
- •3.2. Дії над комплексними числами
- •3.3. Піднесення до степеня і добування кореня
- •4.1. Поліноми від однієї змінної
- •Г) Найбільший спільний дільник
- •Д) Найменше спільне кратне
- •4.3.Поліноми над числовими полями
- •4.4. Поліноми від багатьох змінних
- •Б) Симетричні поліноми
- •5.1. Поняття матриці
- •5.2. Дії над матрицями
- •6.1. Визначники малих порядків
- •6.2. Поняття визначника n-го порядку
- •6.3. Властивості визначника n-го порядку
- •6.4. Обчислення визначників n-го порядку
- •7.1. Загальні поняття
- •7.2. Способи розв’язування систем лінійних рівнянь
- •7.3. Матрична форма запису системи лінійних рівнянь
- •8.1. Поняття векторного простору, його розмірність і базис
- •8.3. Підпростори векторного простору
- •8.4. Лінійні перетворення у векторному просторі
- •8.5. Власні вектори і власні значення лінійного перетворення а) Інваріантні підпростори
- •Звідси із лінійної незалежності векторів e1, e2, …, en випливає:
- •9.1. Поняття евклідового простору
- •9.2. Ортонормований базис
- •9.3. Лінійні перетворення в евклідовому просторі
- •Властивості:
- •10.1. Лінійна функція (форма)
- •10.2. Поняття білінійної та квадратичної функції
- •10.3. Зведення квадратичної форми до суми квадратів
- •10.4. Закон інерції квадратичних форм
- •10.5. Класифікація квадратичних форм
- •10.6. Білінійні і квадратичні форми в евклідовому просторі
- •10.7. Зведення рівняння другого порядку до канонічного вигляду
- •Виконаємо лінійне перетворення
- •11.2. Зведення матриць до жорданової нормальної форми
- •Необхідна і достатня умова зведення матриць до діагонального вигляду
Відображення
При
заданих множинах X
і Y
відображення f
із областю визначення X
і областю значень Y
ставить у
відповідність кожному елементу
 елемент
елемент .
Символічний запис:
.
Символічний запис:
 або
або
 .
.
У
випадку
 відображенняf
називають перетворенням
f
множини X
в себе.
відображенняf
називають перетворенням
f
множини X
в себе.
Образом
при відображенні f
називається множина всіх елементів
 .
ПозначаєтьсяIm
f
(Im
– від image
–
англ.).
Символічний запис:
.
ПозначаєтьсяIm
f
(Im
– від image
–
англ.).
Символічний запис:
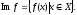
Множина
 називаєтьсяпрообразом
елемента
називаєтьсяпрообразом
елемента
 .
Аналогічно вводиться поняттяпрообразу
множини
.
Аналогічно вводиться поняттяпрообразу
множини

Відображення
 називаєтьсясюр’єктивним
(або відображенням на),
якщо кожен елемент множини Y
має прообраз, тобто якщо
називаєтьсясюр’єктивним
(або відображенням на),
якщо кожен елемент множини Y
має прообраз, тобто якщо
 .
.
Відображення
 називаєтьсяін’єктивним,
якщо різним елементам із прообразу
співставляються різні елементи із
образу, тобто якщо із
називаєтьсяін’єктивним,
якщо різним елементам із прообразу
співставляються різні елементи із
образу, тобто якщо із
 випливає
випливає .
.
Відображення
 називаєтьсябієктивним
або взаємно
однозначним,
якщо воно одночасно сюр’єктивне та
ін’єктивне.
називаєтьсябієктивним
або взаємно
однозначним,
якщо воно одночасно сюр’єктивне та
ін’єктивне.
Два
відображення f
та g
називаються рівними,
якщо їх відповідні області визначення
та значень співпадають, причому

Одиничним
(або тотожнім)
відображенням
 називається відображення, яке переводить
кожний елемент
називається відображення, яке переводить
кожний елемент в себе.
в себе.
Відображення
 називаєтьсявкладенням,
якщо, при
називаєтьсявкладенням,
якщо, при
 воно кожному елементу
воно кожному елементу ставить у відповідність той же елементx,
але вже в множині Y.
ставить у відповідність той же елементx,
але вже в множині Y.
Відображення
 називаєтьсязвуженням
(або обмеженням)
відображення
називаєтьсязвуженням
(або обмеженням)
відображення
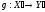 ,
якщо
,
якщо і
і В свою чергу відображенняg
називається продовженням
відображення f.
В свою чергу відображенняg
називається продовженням
відображення f.
Добутком
(або композицією)
двох відображень
 і
і називається відображення
називається відображення ,
яке визначається умовою
,
яке визначається умовою

Зміст цієї операції добре видно із трикутної діаграми
f*g
Z
X
g
f
Y
Ця
діаграма комутативна, оскільки результат
переходу від X
до Z
не залежить від того, чи здійснюється
він з допомогою
 ,
чи використовується проміжний етапY.
,
чи використовується проміжний етапY.
Ясно,
що добуток визначений не для будь-яких
відображень f
і g,
необхідною умовою для його існування
є спільна для цих відображень множина
Y.
Для простоти замість
 пишуть просто
пишуть просто
Композиція
відображень в загальному некомутативна,
тобто

Композиція
відображень асоціативна,
тобто якщо
 то
то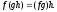 Дійсно,
Дійсно,
Нехай
 і
і – деякі відображення, такі що композиції
– деякі відображення, такі що композиції і
і визначені. Якщо
визначені. Якщо ,
тоf
називається лівим
оберненим
до g,
а g
– правим
оберненим
до f
. Якщо ж
,
тоf
називається лівим
оберненим
до g,
а g
– правим
оберненим
до f
. Якщо ж
 ,
тоg
називається двостороннім
оберненим
до f
(а f
– до g)
і позначається
,
тоg
називається двостороннім
оберненим
до f
(а f
– до g)
і позначається
 .
Обернене до себе має тільки взаємно
однозначне (бієктивне) відображенняf,
причому це обернене відображення
.
Обернене до себе має тільки взаємно
однозначне (бієктивне) відображенняf,
причому це обернене відображення
 теж бієктивне.
теж бієктивне.
1.3. Бінарні відношення на множині
а) Властивості бінарних відношень
Бінарне
відношення
 на множиніА
називається рефлексивним,
якщо
на множиніА
називається рефлексивним,
якщо
 ,
тобто коли кожен елемент множини
перебуває у цьому відношенні сам із
собою.
,
тобто коли кожен елемент множини
перебуває у цьому відношенні сам із
собою.
Відношення
 називаютьнерефлексивним,
якщо в множині А
існує елемент х,
який не перебуває у відношенні
називаютьнерефлексивним,
якщо в множині А
існує елемент х,
який не перебуває у відношенні
 сам із собою:
сам із собою:
Відношення
 називаєтьсяантирефлексивним,
якщо для будь-якого
називаєтьсяантирефлексивним,
якщо для будь-якого
 має місце
має місце
Ясно, що антирефлексивне відношення є нерефлексивним, але нерефлексивне не завжди є антирефлексивним.
Бінарне
відношення
 на множиніА
називається симетричним,
якщо
на множиніА
називається симетричним,
якщо

Відношення
 називаютьнесиметричним
(асиметричним),
якщо
називаютьнесиметричним
(асиметричним),
якщо
 .
.
Відношення
 називаєтьсяантисиметричним,
якщо виконується умова
називаєтьсяантисиметричним,
якщо виконується умова

Відношення
 називаєтьсятранзитивним,
якщо
називаєтьсятранзитивним,
якщо


Відношення
 називаєтьсядосконалим,
якщо
називаєтьсядосконалим,
якщо
 виконується
виконується

Приклади
Відношення „менше” на множині дійсних чисел антирефлексивне, антисиметричне, транзитивне і досконале.
Відношення „не менше” на множині дійсних чисел рефлексивне, антисиметричне, транзитивне і досконале.
Відношення „бути сином” на множині чоловіків антирефлексивне, несиметричне, не транзитивне, не досконале.
б) Відношення еквівалентності
Відношення
 називається відношеннямеквівалентності,
якщо воно рефлексивне, симетричне і
транзитивне.
називається відношеннямеквівалентності,
якщо воно рефлексивне, симетричне і
транзитивне.
Приклади
Відношення рівності.
Відношення подібності геометричних фігур.
Розбиттям
непорожньої множини А
називається сукупність
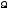 непорожніх підмножинХ
множини А
таких, що:
непорожніх підмножинХ
множини А
таких, що:
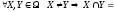 ø.
ø.Об’єднання всіх підмножин Х множини А дорівнює множині А.
Задавши
на множині А
відношення еквівалентності ,
можна утворити розбиття
,
можна утворити розбиття множиниА
на класи еквівалентних елементів так,
щоб для будь-яких
множиниА
на класи еквівалентних елементів так,
щоб для будь-яких
 ,
які належать до одного класу, справджувалось
,
які належать до одного класу, справджувалось ,
а для будь-яких
,
а для будь-яких ,
які належать до різних класів,
справджувалось
,
які належать до різних класів,
справджувалось
Приклади
Відношення еквівалентності
 – „бути подібним” розбиває множину
всіхn-кутників
площини на класи подібних між собою
n-кутників.
– „бути подібним” розбиває множину
всіхn-кутників
площини на класи подібних між собою
n-кутників.
Відношення еквівалентності
 – „навчатися на одному факультеті”
розбиває множину студентів університету
на класи еквівалентності – факультети.
– „навчатися на одному факультеті”
розбиває множину студентів університету
на класи еквівалентності – факультети.
в) Відношення порядку
Відношення
 називають відношеннямстрогого
порядку,
якщо воно антирефлексивне, антисиметричне
і транзитивне.
називають відношеннямстрогого
порядку,
якщо воно антирефлексивне, антисиметричне
і транзитивне.
Приклади
Відношення „бути старшим” на множині людей є відношенням строгого порядку.
Відношення „ділиться на” на множині натуральних чисел є відношенням нестрогого порядку.
Множину, на якій задано відношення порядку, називають впорядкованою.
Спільною рисою всіх відношень порядку є властивість транзитивності.
До нетранзитивних відношень належать відношення толерантності, які характеризуються властивостями рефлективності і симетричності.
Лекція 2. Принцип математичної індукції. Підстановки.
Основні алгебраїчні структури
