Виконаємо лінійне перетворення

_,

_.

Легко перевірити_, що це перетворення ортогональне і переводить попереднє рівняння в нове:

_.

Після цього перетворення

приводить до рівняння:

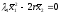, (6)

або

(),

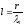якому відповідає параболічний циліндр.

Рівняння (5) і (6) є частинними випадками рівняння

, (7)

в якому – характеристичні числа матриці А (з яких одне може бути нулем),– якась константа, а– координати довільної точки поверхні в деякій ортогональній системі координат. Рівняння (7) називаютьканонічним рівнянням нецентральної поверхні другого порядку.

Приклад

Написати канонічне рівняння поверхні другого порядку

,

визначити її тип і знайти відповідне невироджене перетворення (або канонічну систему координат).

а) Зведемо спочатку до канонічного вигляду (суми квадратів) квадратичну форму .

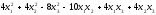–матриця цієї квадратичної форми.

Характеристичне рівняння: .

Характеристичні корені: .

Отримаємо: .

б) Перейдемо до “нових” координат в лівій частині (запишемо лінійну частину в тому ж канонічному базисі):,

, – матриця переходу від“старого” базису до канонічного.

Власні вектори (ортонормований базис):

Матриця переходу

Тоді , або

Підставляємо і отримуємо:

.

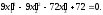
в) Виконаємо зсув за змінною :

, де

Рівняння поверхні: .

Канонічний вигляд рівняння поверхні:

.

Це рівняння гіперболічного циліндра.

г) Результуюче лінійне перетворення:

Канонічна система координат:

Початок:

базис:

Лекція 11. Нормальні форми матриці

11.1. Жорданова нормальна форма матриці

До діагонального вигляду зводиться, як відомо, матриця не кожного лінійного перетворення. Тому виникає питання про інший канонічний вигляд, до якого може бути зведена матриця довільного лінійного перетворення. В комплексному просторі, як і в довільному алгебраїчно замкненому полі, канонічним виглядом матриці є так звана нормальна форма Жордана. Розглянемо її.

Жордановою кліткою називається квадратна матриця вигляду

,

в якій на головній діагоналі знаходиться одне і те ж число , над головною діагоналлю – всюди число 1, а всі решта елементи – нулі.

Приклади

, ,– жорданові клітки 1, 2 і 3 порядків.

Характеристичний поліном перетворення, матрицею якого є жорданова клітка порядку , дорівнює . Він має єдине власне значення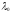кратності, і всі його власні вектори колінеарні. Це означає, що матрицяперетворенняприні в якому базисі не зводиться до діагонального вигляду.

Жордановою матрицею називається матриця вигляду

,

де – жорданові клітки деяких (не обов’язково різних) порядків, всі інші клітки – 0. Числає власними значеннями перетворенняз матрицею.

Діагональні матриці є частинним випадком жорданових матриць (у них жорданові клітки мають порядок 1).

Квадратні матриці порядку , елементами яких є поліноми довільних степенів від однієї невідомоїз коефіцієнтами із поля, називаютьсяполіноміальними матрицями або 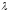-матрицями.

-матриці Ата Вназиваютьсяеквівалентними, якщо від матриці А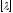до матриці Вможна перейти шляхом скінченної кількості елементарних перетворень.

Канонічною -матрицею називається-матриця, яка володіє властивостями:

1. вона є діагональною, тобто має вигляд ;

2. кожний поліном націло ділиться на поліном;

3. кожний поліном – зведений.

Теорема 1. Будь-яка -матриця з допомогою елементарних

перетворень зводиться до канонічного вигляду, причому

однозначно.

Доведення.

Нехай задана довільна -матриця А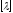порядку. Зафіксуємо деякеk і розглянемо всі мінори-го порядку матриці А. Отримаємо скінченну систему поліномів від. Найбільший спільний дільник цієї системи поліномів (у зведеному вигляді) позначимо. Таким способом віднайдемо набір поліномів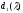,, …,⁽*⁾, визначених однозначно.

Якщо матриця А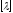має рангr, то =…== 0. Очевидно, щоне змінюється при виконанні в матриці Аелементарних перетворень. Таким чином, всім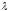-матрицям, еквівалентним матриці А, відповідає один і той же набір поліномів⁽*⁾, тому для знаходження цих поліномів (а, значить, і відповідних мінорів) скористаємось найпростішою (канонічною) матрицею.

Ясно, що мінор k-го порядку, який знаходиться в лівому верхньому куті матриці, дорівнює добутку діагональних елементів ⁽**⁾. Якщо в канонічній матриці вибрати мінор k-го порядку, який знаходиться в рядках з номерами () і в стовпчиках з тими ж номерами, то цей мінор дорівнює добутку, який, очевидно, ділиться на⁽**⁾, оскільки із випливає, ізвипливаєі т.д. І, нарешті, якщо в канонічній матриці вибрати мінорk-го порядку, в якому номери рядків і стовпчиків не співпадають, то цей мінор містить нульовий рядок і тому дорівнює нулю, тобто теж ділиться на ⁽**⁾. Таким чином, добуток ⁽**⁾ і є найбільшим спільним дільником всіх мінорівk-го порядку канонічної матриці, а, значить, і вихідної матриці А, тобто=,k=1,2,…,n. Ясно, що =.

Із єдиності набору поліномів ⁽*⁾ випливає однозначність визначення поліномів . Якщо ранг матриці Адорівнюєr, то ≠0, але=0, звідки=0. Тоді приk<n =…==0. Якщо ж, то

.

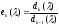Отримана формула дає можливість безпосереднього знаходження поліномів , які називаютьінваріантними множниками матриці А. ▲

Мінімальним поліномом матриці А називається зведений незвідний поліном, для якого матриця А є коренем.

Знайдемо канонічний вигляд для характеристичної матриці довільної жорданової матриці порядку. Спочатку зробимо це для характеристичної матриці

однієї жорданової клітки порядку . Обчислюючи визначник цієї матриці і враховуючи, що старший коефіцієнт поліномамає бути рівним 1, отримаємо. З другого боку, серед мінорів-го порядку матриці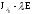є мінор, рівний 1, зокрема, той, що отримується після закреслення першого стовпчика і останнього рядка цієї матриці, звідки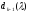=1. Тому, згідно означення, канонічним виглядом для вибраної клітки є наступна-матриця-го порядку:

. (1)

Теорема 2. Якщо поліноми із кільця –попарно

взаємно прості, то має місце така еквівалентність:

~.

Доведення.

Скористаємось методом математичної індукції за t. Ясно, що достатньо розглянути випадок .

Оскільки поліноми – взаємно прості, то в кільцііснують поліномиі, такі що. Тому

~ ~~~~~~,

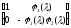що й треба довести. ▲

Розглянемо тепер характеристичну матрицю для жорданової матриці :

(2)

Тут – одинична матриця того ж порядку, що й клітка .

Нехай жорданові клітки матриці відносяться до таких різних чисел:, де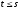. До числавідноситьсяжорданових кліток. Нехай порядки цих кліток (розміщені в незростаючому порядку) рівні . (*)

Застосування елементарних перетворень до тих рядків і стовпчиків матриці, які проходять через клітку цієї матриці, не зачіпатиме, звичайно, інших діагональних кліток. Тому в матриці (2) можна за допомогою елементарних перетворень замінити кожну клітку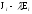відповідною канонічною кліткою вигляду (1). Іншими словами, матрицяеквівалентна діагональній матриці, на діагоналі якої (крім певної кількості одиниць) знаходяться також деякі поліноми, які відповідають всім жордановим кліткам:

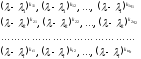(3)

Місця знаходження цих поліномів на діагоналі не вказані, оскільки в будь-якій діагональній матриці діагональні елементи можна довільно переставляти з допомогою перестановок рядків і однойменних стовпчиків.

Нехай – найбільше серед чисел. Позначимо черездобуток поліномів, які знаходяться в-му стовпчику таблиці (3):

. (4)

Якщо при цьому в -му стовпчику є порожні місця (для деякихможе виявитись, що), то відповідні множники в (4) вважаються рівними 1. Оскільки числаза умовою різні, то степені лінійних двочленів, що знаходяться в-му стовпчику таблиці, попарно взаємно прості. Тому (на основі теореми 2) вони з допомогою елементарних перетворень можуть бути замінені в результуючій діагональній матриці їх добуткомі деяким числом одиниць. Виконавши це для всіх, отримаємо матрицю

, (5)

яка і буде шуканим канонічним виглядом характеристичної матриці . Дійсно, старші коефіцієнти поліномів, які знаходяться на головній діагоналі, рівні 1, і кожний з цих поліномів націло ділиться на попередній із-за умови (*).

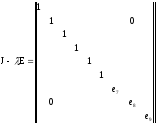
Приклад

Знайти канонічну форму характеристичної матриці до жорданової матриці J:

.

Для цієї жорданової матриці 9-го порядку таблиця поліномів має вигляд:

.

Тому інваріантними множниками матриці будуть поліноми, тоді як.

.

Із означення подібності матриць і з побудови канонічного вигляду характеристичної до жорданової матриці випливає очевидний висновок: дві жорданові матриці подібні тоді і тільки тоді, якщо вони складаються із одних і тих же жордановим кліток (тобто відрізняються тільки розміщенням цих кліток вздовж головної діагоналі).

Із цього твердження випливає:

1. жорданова нормальна форма визначається для матриці однозначно (з точністю до розміщення жорданових кліток вздовж головної діагоналі);

2. жорданова матриця, подібна до діагональної матриці, сама діагональна;

3. дві діагональні матриці подібні тоді і тільки тоді, якщо вони отримуються одна з одної перестановкою чисел, які знаходяться на головній діагоналі.