Звідси із лінійної незалежності векторів e1, e2, …, en випливає:

а₁₁х₁+а₁₂х₂+…+а_1пх_п=λх₁,

а₂₁х₁+а₂₂х₂+…+а_2пх_п=λх₂,

………………………………

а_п1х₁+а_п2х₂+…+а_ппх_п=λх_п,

звідки:

Для існування ненульового розв’язку цієї однорідної системи необхідно і достатньо, щоб її визначник дорівнював нулю:

Ліва частина останньої рівності являє собою поліном п-го степеня відносно λ, який називається характеристичним поліномом перетворення A в базисі е. Він є визначником матриці А-λЕ.

Таким чином, доведено, що кожне власне значення перетворення A є коренем його характеристичного полінома. І навпаки, кожний корінь характеристичного полінома перетворення A буде його власним значенням (відповідні власні вектори знаходяться із останньої системи, яка в даному випадку рівності визначника нулю обов’язково має ненульові розв’язки).

Теорема 2. Характеристичний поліном лінійного перетворення

не залежить від вибору базису.

Доведення.

Характеристичний поліном перетворення A в базисі е нехай буде =|А-λЕ|. Нехай новий базис утворюється із старого за допомогою матриці С. Тоді характеристичний поліном перетворенняA в базисі має вигляд:

▲

Запишемо характеристичний поліном перетворення A:

Видно, що α₁=а₁₁+а₂₂+...+а_пп, тобто дорівнює сумі діагональних елементів матриці А (ця сума називається слідом матриці А). З другого боку, є визначником матриці А. Звідси випливає, щодля того, щоб перетворення A було невиродженим, необхідно і достатньо, щоб φ(0) було відмінне від нуля, тобто щоб перетворення A не мало нульових власних значень.

Приклад

Знайти власні значення і власні вектори лінійного перетворення A з матрицею

А=

Характеристичний поліном матриці А має вигляд:

Власні значення перетворення A є коренями характеристичного полінома: λ₁=-1, λ₂=5.

Власні вектори знаходять із системи рівнянь:

а) λ₁=-1. тому в ролі першого

власного вектора можна взяти вектор f₁=(-1;2) або кратний йому;

б) λ₂=5. тому в ролі другого власного

вектора можна взяти вектор f₂=(1;1) або кратний йому.

Лекція 9. Евклідові простори

9.1. Поняття евклідового простору

а) Скалярний добуток

Як відомо, у векторному просторі відсутній спосіб вимірювання довжин векторів і кутів між ними. Для розв’язання цієї проблеми скористаємось поняттям скалярного добутку.

У звичайному тривимірному векторному просторі скалярним добутком двох векторів називається добуток їх довжин, помножений на косинус кута між ними. Для векторів х та у їх скалярний добуток позначається (х, у). Отже,

(x, y)=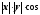(x,y).

Властивості:

1. x, yV [(x, y)=(y, x)]. В комплексному просторі (х, у)=

2. x, yV, [(αx, y)=α(x, y)].

3. x, y, zV [(x+y, z)=(x, z)+(y, z)].

4. xV [(x, x) ≥ 0, причому із (х, х)=0 випливає х=θ].

У векторному просторі V вважається заданим скалярний добуток, якщо кожній парі векторів x, y V поставлено у відповідність число (х, у) так, що виконуються умови 1–3.

Векторний простір, в якому заданий скалярний добуток, що задовольняє умовам 1–4, називається евклідовим простором.

Із рівностей 1–3 випливають співвідношення:

2′. (x, αy)=(αy, x)=α(y, x)=α(x, y).

3′. (z, x+y)=(x+y, z)=(x, z)+(y, z)=(z, x)+(z, y).

Приклад

Якщо в п-вимірному векторному просторі вибрано деякий базис e=(e₁, e₂, …, e_n), в якому вектори х та у мають наступні розклади:

x=x₁e₁+x₂e₂+…+x_ne_n,

y=y₁e₁+y₂e₂+…+y_ne_n,

то їх скалярний добуток визначається рівністю:

(x,y)=x₁y₁+x₂y₂+…+x_ny_n

(властивості 1–4 перевіряються безпосередньо).

Довжиною вектора х називається корінь квадратний із його скалярного квадрата:

Кут між векторами х та у визначається рівністю

.

б) Нерівність Коші-Буняковського

x, yV або.

Доведення.

Якщо α – довільне дійсне число , то для вектора х-αу (із умови 4) маємо

(х-αу, х-αу) ≥ 0,

звідки (із 1–3) отримаємо:

(х,х)-2α(х,у)+α²(у,у) ≥ 0.

Отримано квадратний тричлен відносно α. Оскільки він має бути невід’ємним при всіх α, то його дискримінант недодатний, тобто

що й треба довести. ▲

Очевидним є те, що рівність досягається (умова 4) тільки при х-αу=θ, тобто х = αу (вектори х та у пропорційні).

Оскільки із нерівності Коші-Буняковського випливає, що, то це підтверджує правомірність користування формулою для знаходженняcos.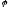

Вектори х та у, скалярний добуток яких дорівнює нулю, називаються ортогональними.