6.1. Визначники малих порядків

Поняття визначника матриці виникло у зв’язку із проблемою виведення формул розв’язків систем лінійних рівнянь.

В системі двох лінійних рівнянь з двома невідомими

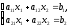
хоча б один із коефіцієнтів чивідмінний від нуля. Нехай(інакше переставимо рівняння місцями). Для розв’язання системи віднімемо від другого рівняння, помноженого на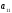, перше, помножене на, і отримаємо:

.

Якщ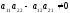о , то.

Підставивши значення х₂ в систему, знайдемо

.

Якщо тепер розглянути матрицю із коефіцієнтів системи

А,

то вираз (різниця добутків елементів головної і побічної діагоналей) називаютьвизначником або детермінантом цієї матриці і позначають

=А=|А|=.

Різниця є визначником матриці =, а – визначником матриці=.

Тоді ,, тобто,.

Розглянемо тепер систему трьох лінійних рівнянь з трьома невідомими:

Припустимо, що ця система має розв’язки і – один із її розв’язків. Тоді

справедливі рівності

Помноживши першу рівність на число , другу – на, третю – на, і додавши отримані вирази, отримаємо рівність

Коефіцієнт при називаютьвизначником матриці А

і позначають

=А=|А|==

=.

Правило обчислення додатніх і від’ємних членів визначника третього порядку називають правилом Саррюса і схематично подають так:

Приклад

=

=.

Очевидно, що =.

Видно, що права частина виразу для теж є визначником третього порядку. Це визначник матриці, отриманої із матриці А заміною її першого стовпчика стовпчиком вільних членів системи.

Тобто, (приd).

Аналогічно, помноживши рівності початкової системи відповідно на -,-,-і додавши їх, знайдемо вираз для.

Нарешті, помноживши рівності початкової системи відповідно на

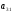-,-,-, знайдемо вираз для.

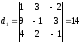
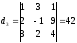
Приклад

Розв’язати систему

=(1+27-8)-(6-6+6)=14.

. ..

=

Відповідь: 1; 2; 3.

6.2. Поняття визначника n-го порядку

Встановимо тепер загальне правило побудови визначника довільного n-го порядку.

Визначником матриці першого порядку, утвореної числом, називають число.

Визначником матриці другого порядку називають число

.

Визначником матриці третього порядку називають

число =.

Якщо позначити визначник 3-го порядку (ліва частина) через 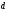, а визначники 2-го порядку (в правій частині) черезто матимемоТутє визначником квадратної матриці 2-го порядку, яка утворюється викресленням у матриці 3-го порядку 1 рядка таj-го стовпчика. Отже, щоб знайти визначник матриці 3-го порядку, треба визначники матриць 2-го порядку, що утворюються внаслідок викреслення в цій матриці першого рядка та першого, другого і третього стовпчиків, помножити відповідно на перший, другий і третій елементи першого рядка матриці, поставити перед добутками почергово знаки плюс, мінус і потім додати.

Очевидно, що за аналогічним алгоритмом можна знайти і визначник матриці 2-го порядку: 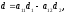деі– визначники матрицьівідповідно.

Отримане правило покладене в основу визначення поняття визначника n-го порядку.

Визначником матриці An-го порядку

називають число ,

де – визначник матриці порядкуn-1, яка утворюється внаслідок викреслення в матриці А першого рядка і j-го стовпчика.

Позначають А=.

Якщо в матриці А викреслити і-й рядок та j-й стовпчик, тобто рядок і стовпчик, на перетині яких знаходиться елемент , то отримається квадратна матриця (n-1)-го порядку, визначник якої називають мінором матриці А, який відповідає елементові , або мінором елементау визначнику, і позначається символом. Тобто,

=.

Тоді А =|А|=.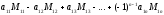

Звідси випливає означення визначника n-го порядку:

визначником квадратної матриці n-го порядку називають алгебраїчну суму добутків елементів її першого рядка на відповідні їм мінори, взятих почергово із знаками плюс та мінус.

Розглянемо тепер ще один підхід до означення поняття визначника n-го порядку.

Теорема. Для довільної квадратної матриці

А

А =|А|=,

де – кількість інверсій у перестановці з чисел 1, 2, ..., n, причому підсумовування ведеться за всіма n! перестановками із n чисел.

Доведення.

Скористаємось методом математичної індукції за n. Нехай n=2.

Припустимо, що теорема справедлива для матриць порядку n-12 і доведемо її справедливість для довільної матриці порядкуn.

За відомою нам формулою

А =|А|==.

Тут мінор 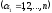є мінором (n-1)-го порядку, тому, згідно індуктивного припущення, він виражається через свої елементи так:

,

де підсумовування ведеться за всіма перестановками з (n-1) чисел 1, 2, …, α₁-1, α₁+1, …, n.

Із чисел α₁, α₂, …, α_n, крім пар, утворюваних числами α₂, α₃, …, α_n, можна утворити ще тільки пари (α₁,α₂), (α₁,α₃),…, (α₁,α_n), серед яких тільки α₁-1 утворюють інверсії, оскільки серед чисел , менших відα₁, є тільки α₁-1. Звідси випливає, що N = N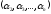+α₁-1, і тому

.

Врахувавши вищесказане, отримаємо:

що й треба довести.

Отже, теорема справедлива для всіх натуральних n. ▲

Добутки називаютьчленами визначника матриці А. Як видно, кожен член визначника матриці n-го порядку є добутком n елементів матриці, взятих по одному з кожного рядка і кожного стовпчика. Знак, із яким член входить до визначника, визначається кількістю інверсій в перестановці, зокрема, парністю цієї перестановки: якщо перестановка парна, то член має знак плюс, якщо непарна – то мінус. Але парність перестановкиспівпадає із парністю підстановки, де 1-й і 2-й рядки є відповідно 1-ми та 2-ми індексами цього члена визначника. Отже, знак членавизначника визначається парністю підстановки, утвореної індексами його елементів.

Враховуючи вищесказане, сформулюємо ще одне рівносильне попередньому означення визначника n-го порядку.

Визначником матриці n-го порядку називається алгебраїчна сума n! членів, якими є всеможливі добутки елементів матриці, взятих по одному з кожного її рядка і кожного стовпчика, причому член береться із знаком плюс, якщо його індекси утворюють парну підстановку, і мінус – якщо непарну.