
- •Множини
- •Відображення
- •1.3. Бінарні відношення на множині
- •2.1. Принцип математичної індукції Аксіома математичної індукції
- •Узагальнення другої форми принципу математичної індукції
- •2.2. Підстановки
- •Основні алгебраїчні структури
- •3.1. Означення комплексного числа
- •3.2. Дії над комплексними числами
- •3.3. Піднесення до степеня і добування кореня
- •4.1. Поліноми від однієї змінної
- •Г) Найбільший спільний дільник
- •Д) Найменше спільне кратне
- •4.3.Поліноми над числовими полями
- •4.4. Поліноми від багатьох змінних
- •Б) Симетричні поліноми
- •5.1. Поняття матриці
- •5.2. Дії над матрицями
- •6.1. Визначники малих порядків
- •6.2. Поняття визначника n-го порядку
- •6.3. Властивості визначника n-го порядку
- •6.4. Обчислення визначників n-го порядку
- •7.1. Загальні поняття
- •7.2. Способи розв’язування систем лінійних рівнянь
- •7.3. Матрична форма запису системи лінійних рівнянь
- •8.1. Поняття векторного простору, його розмірність і базис
- •8.3. Підпростори векторного простору
- •8.4. Лінійні перетворення у векторному просторі
- •8.5. Власні вектори і власні значення лінійного перетворення а) Інваріантні підпростори
- •Звідси із лінійної незалежності векторів e1, e2, …, en випливає:
- •9.1. Поняття евклідового простору
- •9.2. Ортонормований базис
- •9.3. Лінійні перетворення в евклідовому просторі
- •Властивості:
- •10.1. Лінійна функція (форма)
- •10.2. Поняття білінійної та квадратичної функції
- •10.3. Зведення квадратичної форми до суми квадратів
- •10.4. Закон інерції квадратичних форм
- •10.5. Класифікація квадратичних форм
- •10.6. Білінійні і квадратичні форми в евклідовому просторі
- •10.7. Зведення рівняння другого порядку до канонічного вигляду
- •Виконаємо лінійне перетворення
- •11.2. Зведення матриць до жорданової нормальної форми
- •Необхідна і достатня умова зведення матриць до діагонального вигляду
9.3. Лінійні перетворення в евклідовому просторі
а) Перетворення, спряжене до даного
Нехай
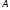 – лінійне перетворення евклідового
простору
– лінійне перетворення евклідового
простору .
Лінійне перетворення
.
Лінійне перетворення ,
для якого при всіхx,
y
,
для якого при всіхx,
y
 V
V
( x,
y)
= (x,
x,
y)
= (x,
 *y),
*y),
називається
спряженим
до
 .
.
Покажемо,
що для кожного лінійного перетворення
 евклідового простору існує спряжене
до нього перетворення
евклідового простору існує спряжене
до нього перетворення ,
матриця якого в довільному ортонормованому
базисі є транспонованою до матриці
перетворення
,
матриця якого в довільному ортонормованому
базисі є транспонованою до матриці
перетворення .
.
Нехай
A=[aij]
– матриця лінійного перетворення
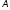 в
орто-нормованому базисі e1,
e2,
…,
en,
А' – матриця, транспонована до А,
в
орто-нормованому базисі e1,
e2,
…,
en,
А' – матриця, транспонована до А,
 – лінійне перетворення з матрицею А' в
тому ж базисі. Тоді, очевидно,
– лінійне перетворення з матрицею А' в
тому ж базисі. Тоді, очевидно,
( ei,
ej)
= (a1ie1
+ a2ie2
+ …
+
anien,
ej)
= aji,
ei,
ej)
= (a1ie1
+ a2ie2
+ …
+
anien,
ej)
= aji,
(ei,
 *ej)
= (ei,
aj1e1
+ aj2e2
+ …
+
ajnen)
= aji,
*ej)
= (ei,
aj1e1
+ aj2e2
+ …
+
ajnen)
= aji,
тобто
для всіх

( ei,
ej)
= (ei,
ei,
ej)
= (ei,
 *ej).
*ej).
Тоді, якщо x = x1e1 + x2e2 + … +xnen i y = y1e1 + y2e2 + … + ynen, то
( x,
y)
= (
x,
y)
= (
 xiei,
xiei,
 yjej)
=
yjej)
=
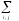 xiyj(
xiyj( ei
ej)
i
ei
ej)
i
(x, *y)
= (
*y)
= ( xiei,
xiei, *
* yjej)
=
yjej)
=
 xiyj(ei,
xiyj(ei, *ej)
=
*ej)
=
 xiyj(
xiyj( ei
ej)
= (
ei
ej)
= (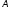 x,
y),
x,
y),
тобто
перетворення
 є спряженим до
є спряженим до
 .
.
Властивості:
 .
.
Доведення.
(x,
 y)
= (
y)
= (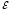 x,
y)
=
(x,
y)
= (x,
x,
y)
=
(x,
y)
= (x,
 y).
y).
 .
.
Доведення.
( x,
y)
= (x,
x,
y)
= (x,
 *y)
= (
*y)
= ( *y,
x)
= (y,
(
*y,
x)
= (y,
( *)*
x)
= ((
*)*
x)
= (( *)*
x,
y).
*)*
x,
y).
 .
.
Доведення.
(x,
( +
+ )*y)
= ((
)*y)
= ((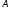 +
+ )x,
y)
= (
)x,
y)
= ( x+
x+ x,
y)
= (
x,
y)
= ( x,
y)+(
x,
y)+( x,
y)=
x,
y)=
=
(x,
 *y)
+ (x,
*y)
+ (x,
 *y)
= (x,
(
*y)
= (x,
( *+
*+ *)y).
*)y).
4.

Доведення.
(x,
(
 )*y)
= ((
)*y)
= ((
 )x,
y)
= (
)x,
y)
= ( (
( x),
y)
= (
x),
y)
= (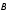 x,
x,
 *y)
= = (x,
*y)
= = (x,
 *(
*(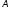 *)y)
= (x,
(
*)y)
= (x,
(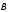 *
* *)y).
*)y).
Якщо
 існує, то
існує, то .
.
Доведення.
 .
.
б) Самоспряжені перетворення
Самоспряженим
(симетричним)
називається перетворення, яке співпадає
зі своїм спряженим, тобто
 .
.
Якщо
A
– самоспряжене перетворення, то
 x,y
x,y V
(
V
( x,
y)=(x,
x,
y)=(x,
 y).
y).
Якщо
матрицею самоспряженого перетворення
 в орто-нормованому базисі є
A=[aij],
тоді A' = A, тобто
aij
=
aji.
Така матриця називається симетричною.
в орто-нормованому базисі є
A=[aij],
тоді A' = A, тобто
aij
=
aji.
Така матриця називається симетричною.
Властивості:
Тотожнє перетворення
 є самоспряженим.
є самоспряженим.
Доведення.
 .
.
Сума самоспряжених перетворень є самоспряженим
перетворенням.
Доведення.
 .
.
Перетворення, обернене до невиродженого самоспряженого перетворення, є самоспряженим перетворенням.
Доведення.
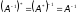 .
.
Добуток самоспряжених перетворень є самоспряженим перетворенням тоді і тільки тоді, коли ці перетворення переставні між собою.
Доведення.
а)
якщо
 ,
, і
і ,
то
,
то ,
тобто
,
тобто .
.
б)
якщо
 ,
, і
і ,
то
,
то ,
тобто
,
тобто –
–
самоспряжене перетворення.
Якщо підпростір
 інваріантний відносно лінійного
перетворення
інваріантний відносно лінійного
перетворення ,
то його ортогональне доповнення
,
то його ортогональне доповнення інваріантне відносно спряженого до
інваріантне відносно спряженого до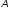 перетворення
перетворення *.
*.
Доведення.
Нехай
х
– довільний вектор із
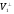 ,у
– довільний вектор із
,у
– довільний вектор із
 .
.
Тоді
( *x,
y)=(x,
*x,
y)=(x, y)
= 0, оскільки
y)
= 0, оскільки
 y
y
 і, значить,х
і, значить,х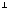
 y.
Значить, вектор
y.
Значить, вектор
 *x
*x ,
і
,
і
 є інваріантним відносно
є інваріантним відносно *.
*.
Наслідок.
Якщо
 – самоспряжене перетворення і
– самоспряжене перетворення і –
підпростір,
–
підпростір,
інваріантний
відносно
 ,
то і
,
то і інваріантний
інваріантний
відносно
 .
.
Всі корені характеристичного полінома самоспряженого перетворення
 дійсні(власні
значення самоспряженого перетворення
дійсні).
дійсні(власні
значення самоспряженого перетворення
дійсні).
Доведення.
( x,
х)
= (λx,
х),
(x,
x,
х)
= (λx,
х),
(x,
 х)
=
х)
=
 = (
= (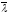 x,
х).
x,
х).
Оскільки
 – самоспряжений, то (
– самоспряжений, то ( x,
х)
= (x,
x,
х)
= (x,
 х),
значить
х),
значить
 ,
тобто
,
тобто – дійсне.
– дійсне.
7. Власні вектори, що відповідають різним власним значенням самоспряженого перетворення, ортогональні.
Доведення.
Нехай
 –власні
значення самоспряженого оператора
–власні
значення самоспряженого оператора
 ,
ах1
та х2
– відповідні їм власні вектори. Тоді
(
,
ах1
та х2
– відповідні їм власні вектори. Тоді
( x1,х2)
= λ1(x1,х2),
(x1,
x1,х2)
= λ1(x1,х2),
(x1, х2)
=
= λ2(x1,х2).
Звідси (
х2)
=
= λ2(x1,х2).
Звідси ( x1,х2)
= (x1,
x1,х2)
= (x1, х2
), оскільки
х2
), оскільки
 – самоспряжений. Тоді
– самоспряжений. Тоді
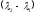 (x1,
х2)
= 0
(x1,
х2)
= 0
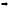 (x1,
х2)
= 0,
(x1,
х2)
= 0,
що й треба було довести.
Матриця самоспряженого перетворення в деякому орто- нормованому базисі зводиться до діагонального вигляду.
Доведення.
Нехай
 – одне із власних значень самоспряженого
перетворення
– одне із власних значень самоспряженого
перетворення
 (
( дійсне). Відповідний власний вектор
позначимо
е1,
тобто
дійсне). Відповідний власний вектор
позначимо
е1,
тобто
 е1=
λ1е1.
Вектор е1
можна вважати одиничним, оскільки
інакше
його можна замінити одиничним власним
вектором
е1=
λ1е1.
Вектор е1
можна вважати одиничним, оскільки
інакше
його можна замінити одиничним власним
вектором
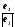 з
тим
же власним значенням
з
тим
же власним значенням
 .
.
Позначимо
через
 одновимірний підпростір, породжений
вектором
е1.
Його ортогональне доповнення
одновимірний підпростір, породжений
вектором
е1.
Його ортогональне доповнення
 буде інваріантним відносно
буде інваріантним відносно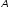 .
Нехай
.
Нехай – (дійсне) власне значення перетворення
– (дійсне) власне значення перетворення в підпросторі
в підпросторі ,
відповідний (одиничний) власний вектор
позначимо
е2.
Тоді
,
відповідний (одиничний) власний вектор
позначимо
е2.
Тоді
 е2=λ2е2.
Нехай
е2=λ2е2.
Нехай
 буде (інваріантним) підпростором,
породженим векторами е1
і
е2.
Тоді підпростір
буде (інваріантним) підпростором,
породженим векторами е1
і
е2.
Тоді підпростір
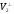 теж інваріантний відносно
теж інваріантний відносно .
Продовжуючи цю побудову, ми знайдемо
.
Продовжуючи цю побудову, ми знайдемо попарно ортогональних (значить, лінійно
незалежних) одиничних власних векторів
перетворення
попарно ортогональних (значить, лінійно
незалежних) одиничних власних векторів
перетворення .
В базисі, що складається із цих векторів,
матриця А перетворення
.
В базисі, що складається із цих векторів,
матриця А перетворення зводиться до діагонального вигляду:
зводиться до діагонального вигляду:
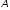 е1
= λ1е1,
е1
= λ1е1,
 е2
= λ2е2,
е2
= λ2е2,
…………..
 еn
= λnеn,
еn
= λnеn,
звідки
А =
 .
.
Геометрично
самоспряжене лінійне перетворення
зводиться до
 розтягів з коефіцієнтами
розтягів з коефіцієнтами вздовж
вздовж координатних осей, спів-напрямлених зе1,
е2,
…,
еn
відповідно.
координатних осей, спів-напрямлених зе1,
е2,
…,
еn
відповідно.
в) Ортогональні перетворення
Лінійне
перетворення
 евклідового простору V
називається ортогональним,
якщо воно зберігає скалярний добуток
векторів,
тобто якщо
евклідового простору V
називається ортогональним,
якщо воно зберігає скалярний добуток
векторів,
тобто якщо
 x,
y
x,
y
 V(
V( x,
x,
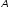 y)
= (x,
y).
y)
= (x,
y).
Це означає , що ортогональне перетворення зберігає довжини векторів та кути між ними (тому ортогональні перетворення іноді називають ізометричними).
Ясно, що ортогональне перетворення переводить довільний ортонормований базис в ортонормований і навпаки.
Властивості:
1.

 *=
*= ,
тобто
,
тобто *=
*=
 -1.
-1.
Доведення.
Якщо
 – ортогональне перетворення і
– ортогональне перетворення і – спряжене до нього перетворення, то
– спряжене до нього перетворення, то x,
y
x,
y
 V
(x,
y)
= (
V
(x,
y)
= (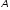 x,
x,
 y)
=
(x,
y)
=
(x,
 *(
*( y))
= (x,
y))
= (x,
 *
* y).
Значить,
y).
Значить,

 або
або .
Із отриманих рівностей видно, щоортогональне
перетворення завжди невироджене.
.
Із отриманих рівностей видно, щоортогональне
перетворення завжди невироджене.
Перетворення, обернене до ортогонального, теж ортогональне.
Доведення.
Якщо
 ,
то
,
то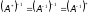 .
.
Сума ортогональних перетворень, в загальному, не є ортогональним перетворенням.
Добуток ортогональних перетворень є ортогональним
перетворенням.
Доведення.
 .
.
Матриця A, для якої A' = A-1, називається ортогональною матрицею.
Визначник ортогональної матриці дорівнює
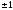 .
.
Доведення.
Із AA' = E випливає: AA'| = |A||A'| = |E| = 1.
Оскільки |A| = |A'| (транспонування не змінює визначника), то
|A|2
= 1 ,
звідки
 .
.
Власні значення ортогонального перетворення дорівнюють
 .
.
Доведення.
Якщо
x
–
власний вектор і
 – відповідне
йому власне значення ортогонального
перетворення
– відповідне
йому власне значення ортогонального
перетворення
 ,
то:
,
то:
(x,
x)
= ( x,
x,
 x)
= (λx,
λx)
= λ2(x,
x),
x)
= (λx,
λx)
= λ2(x,
x),
звідки,
оскільки (x,
x)
≠ 0, отримуємо
 ,
і
,
і .
.
Якщо підпростір
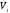 інваріантний відносно ортогонального
перетворення
інваріантний відносно ортогонального
перетворення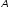 ,
то його ортогональне доповнення
,
то його ортогональне доповнення теж інваріантне відносно
теж інваріантне відносно .
.
Доведення.
Із
ортогональності перетворення
 випливає
випливає
 .
Згідно властивості 5 пункту б підпростір
.
Згідно властивості 5 пункту б підпростір інваріантний відносно перетворення
інваріантний відносно перетворення .
Але тоді цей підпростір інваріантний
і відносно оберненого перетворення,
тобто відносно
.
Але тоді цей підпростір інваріантний
і відносно оберненого перетворення,
тобто відносно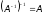 .
.
Приклади
Нехай
 –
ортогональне перетворення прямої
–
ортогональне перетворення прямої
 іе
іе .
Тоді
.
Тоді
 е
е
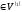 і, значить,
і, значить,
 е
=
λе,
де
е
=
λе,
де
 ,
тобто
,
тобто
 е
=
±е.
Це означає, що
е
=
±е.
Це означає, що
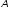 –
або тотожнє
перетворення,
або
центральна симетрія.
–
або тотожнє
перетворення,
або
центральна симетрія.
Нехай
 –
ортогональне перетворення площини,
і А
–
ортогональне перетворення площини,
і А –
його матриця в деякому ортонормованому
базисі. Тоді із А*А=Е,
тобто
–
його матриця в деякому ортонормованому
базисі. Тоді із А*А=Е,
тобто
 ,
отримаємо:
,
отримаємо:
 ,
,
 ,
,
 .
.
Для
перших двох рівностей знайдуться такі
 і
і ,
що:
,
що:
 ,
,
 ,
, ,
, .
.
Тоді
третя рівність дає
 ,
звідки випливає, що
,
звідки випливає, що або
або .
.
В
першому випадку
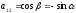 ,
,
 ,
,
і
ми отримаємо:
А ,
,
тобто перетворення A – це поворот на кут α навколо початку координат.
В
другому випадку
 ,
,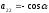 ,
і
А
,
і
А .
.
Ця
матриця – симетрична, значить, ортогональне
перетворення
 є і самоспряженим, тобто в деякому
ортогональному базисі його матриця
зводиться до діагонального вигляду:А
є і самоспряженим, тобто в деякому
ортогональному базисі його матриця
зводиться до діагонального вигляду:А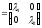 ,
де
,
де
 .
.
Визначник
цієї матриці
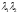 повинен бути рівним:
повинен бути рівним:
 ,
,
значить
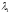 і
і мають різні знаки, тобто матриця
перетворення
мають різні знаки, тобто матриця
перетворення
 зводиться до виглядуА
зводиться до виглядуА .
Це симетрія
відносно прямої,
яка визначається вектором е1
(першим вектором нового базису).
.
Це симетрія
відносно прямої,
яка визначається вектором е1
(першим вектором нового базису).
Таким
чином, ортогональне
перетворення площини
– це або поворот
навколо
початку координат на деякий кут
 (зокрема, тотожнє перетворення або
центральна симетрія – визначник цих
перетворень дорівнює 1) абоосьова
симетрія
(визначник дорівнює -1).
(зокрема, тотожнє перетворення або
центральна симетрія – визначник цих
перетворень дорівнює 1) абоосьова
симетрія
(визначник дорівнює -1).
Лекція 10. Білінійні і квадратичні функції (форми)
