2.1. Принцип математичної індукції Аксіома математичної індукції

Нехай А – множина натуральних чисел, яка має наступні властивості:

1. А.

2. Якщо число kN належить до А, то й наcтупне число належить до А.

Тоді до А належать всі натуральні числа.

Принцип математичної індукції (основна форма)

Якщо деяке твердження Т правильне для числа 1 і якщо з припущення, що воно правильне для натурального числа k, випливає його правильність і для наступного числа , то твердження Т правильне для будь-якого натурального числа n.

Доведення.

Нехай А – множина тих натуральних чисел, для кожного із яких твердження Т правильне. За умовою теореми А, і якщо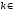А, то й наступне число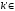А. Тоді, згідно аксіоми індукції, множина А збігається з множиною всіх натуральних чисел. Таким чином, твердженняТ виконується для будь-якого натурального числа.▲

Для доведення справедливості якогось твердження для довільного натурального числа п методом математичної індукції, треба:

1) довести, що твердження справедливе для п=1;

2) припустивши справедливість твердження для n=k, довести його справедливість для

У випадку, коли твердження Т при п=1 не має змісту або неправильне, але стає справедливим при (або взагалі при), використовується інша форма принципу математичної індукції.

Узагальнення основної форми принципу математичної індукції

Якщо деяке твердження Т правильне для натурального числа і якщо з припущення, що воно правильне для натурального числа , випливає його правильність і для наступного числа , то твердження Т правильне для будь-якого натурального числа n.

Друга форма принципу математичної індукції

Якщо деяке твердження Т правильне для числа 1 і якщо з припущення, що воно правильне для всіх натуральних чисел, менших ніж k, випливає його правильність і для числа k, то твердження Т правильне для будь-якого натурального числа п.

Узагальнення другої форми принципу математичної індукції

Якщо деяке твердження Т правильне для натурального числа і якщо з припущення, що воно правильне для всіх натуральних чисел, менших ніж k, випливає його правильність і для числа k, то твердження Т правильне для будь-якого натурального числа.

2.2. Підстановки

а) Перестановки

Перестановкою із n чисел 1, 2,…, n (чи n символів) називається будь-яке їх розташування в деякому визначеному порядку.

Перетворення перестановки, при якому в ній поміняно місцями довільні два символи (необов’язково сусідні), а всі решту символи залишено на місці, називається транспозицією.

Числа i та j утворюють в перестановці інверсію, якщо i>j, але i знаходиться в цій перестановці раніше за j. Перестановка називається парною, якщо її символи утворюють парну кількість інверсій, і непарною – в протилежному випадку. Наприклад, перестановка (3, 2, 1, 5 ,4) є парною (чотири інверсії), а (2, 3, 5, 4, 1) – непарною (п’ять інверсій).

Властивості:

1. Кількість різних перестановок із n символів дорівнює добутку 1·2·…·n = n!

Доведення.

У загальному вигляді перестановки із n символів i₁, i₂,…, i_n кожне із i_k є одним із чисел 1, 2,…, n, причому числа не повторюються. Оскільки в ролі i₁ можна взяти довільне із чисел 1, 2,…, n, отримається n різних варіантів. При вибраному i₁ в ролі i₂ можна взяти тільки n-1 із чисел, що залишилися, тому кількість різних способів вибрати символи i₁ та i₂ дорівнюватиме n(n-1). Подальші аналогічні міркування призведуть до потрібного результату. ▲

2. Від довільної перестановки із n символів до будь-якої іншої перестановки із тих же елементів можна перейти з допомогою декількох транспозицій.

Доведення.

Починаючи з довільної перестановки, всі n! перестановок із n символів можна розмістити в такому порядку, що кожна наступна отримана із попередньої однією транспозицією. ▲

3. Кожна транспозиція змінює парність перестановки.

Доведення.

Якщо перестановка має вигляд …, i, j,…, тобто транспоновані символи i та j є сусідніми, то в результаті транспозиції отримаємо нову перестановку …, j, i,…, в якій символи i та j утворюватимуть із нерухомими символами ті ж інверсії, що й у попередній. Від переставляння символів i та j кількість інверсій зміниться на одну (якщо інверсії не було, то вона з’явиться, якщо ж була, то зникне), що і змінить парність перестановки.

Якщо між транспонованими символами i та j розміщено ще t символів, тобто перестановка має вигляд …, i, k₁, k₂, …, k_t, j,…, то транспозицію символів i та j можна отримати в результаті 2t+1 транспозицій сусідніх елементів (t для переміщення i на місце k_t, 1 для переставлення місцями і та j, t для переміщення j з позиції k_t на місце i), в результаті чого утвориться перестановка …, j, k₁, k₂, …, k_t, i,…, яка матиме протилежну парність до початкової.

4. При n2 кількість парних перестановок із n символів дорівнює кількості непарних, тобто дорівнює n!

Доведення.

Після впорядкування всіх перестановок із n символів так, що кожна наступна отримується із попередньої однією транспозицією, сусідні перестановки матимуть протилежні парності, а оскільки число n! парне, то кількість парних перестановок дорівнюватиме кількості непарних.

б) Підстановки

Дві перестановки із n символів, записані одна під одною, визначають деяке взаємно однозначне відображення множини перших n натуральних чисел на себе.

Довільне взаємно однозначне відображення А множини перших n натуральних чисел на себе називається підстановкою n-го степеня. Позначається так:

.

Тут α_i – число, в яке при підстановці А переходить число i, і=1, 2,…, n. Читають так: при підстановці А число і₁ переходить в ,і₂ – в ,…,і_n – в .

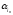Від одного запису підстановки А до іншого можна перейти з допомогою декількох транспозицій стовпчиків.

Приклад

, ,.

Завжди можна отримати запис підстановки у вигляді , при якому різні підстановки відрізняються одна від одної тільки нижніми перестановками, звідки випливає, щокількість підстановок n-го степеня дорівнює кількості перестановок із n символів, тобто дорівнює n!

Підстановка Е називається тотожньою або одиничною.

Підстановка називається парною, якщо парності верхньої і нижньої її перестановок співпадають (або сума інверсій у верхній і нижній перестановках є парною). В іншому випадку підстановку називають непарною.

Кількість непарних підстановок n-го степеня дорівнює кількості парних, тобто дорівнює n! Цей висновок випливає із можливості запису верхньої перестановки довільної підстановки у вигляді частини натурального ряду і властивості 4 перестановок з n елементів.

Добутком двох підстановок n-го степеня називається підстановка n-го степеня, отримана в результаті послідовного виконання цих підстановок.

Приклади

АВ ==.

Множення підстановок n-го степеня при n3 некомутативне.

ВА = =

(порівняти з попереднім).

Множення підстановок асоціативне, тобто (АВ)С=А(ВС).

Так, якщо символ і₁ при підстановці А переходить в і₂, символ і₂ при підстановці В переходить в і₃, а і₃ при підстановці С переходить в і₄, то при підстановці АВ символ і₁ переходить в і₃, при підстановці ВС символ і₂ переходить в і₄, тому при обох підстановках (АВ)С та А(ВС) символ і₁ переходить в символ і₄.

Для будь-якої підстановки А: АЕ=ЕА=А.

Оберненою для підстановки А називається така підстановка А^-1 того ж степеня, що АА^-1 = А^-1А = Е.

Очевидним є те, що оберненою для підстановки A= є підстановка А^-1=, отримана із А переставленням нижнього і верхнього рядків.

Циклічною підстановкою (циклом) довжиною k називається така підстановка, при повторенні якої k разів кожен з її символів переходить в себе.

Приклад

Підстановка 8-го степеня має цикл (136285) довжиною 6.