9.2. Ортонормований базис

а) Процес ортогоналізації

Базис е₁, е₂, ..., е_п евклідового векторного простору називається ортогональним, якщо при.

Якщо, крім того, приі=1, 2, ..., п, то базис називається ортонормованим.

Теорема1. Ортонормована система векторів лінійно незалежна.

Доведення.

Нехай ненульові вектори х₁, х₂, ..., х_k попарно ортогональні: (х_і, x_j)=0 при Розглянемо рівність

α₁х₁+α₂х₂+...+α_kx_k=θ.

Помножимо обидві частини скалярно на х_і, і=1, 2, ..., k. Отримаємо

α₁(х₁, х_і)+α₂(х₂, х_і)+...+ α_k(x_k, x_i)=0,

звідки із врахуванням (x_i, x_j)=0 при тапри всіхі=1, 2,..., k) випливає, що α_і=0 при і=1, 2, ..., k, що й треба довести. ▲

Теорема2. В кожному евклідовому просторі існують ортонормовані

базиси.

Доведення.

Нехай е₁, е₂, ..., е_п – довільний базис простору V. Покладемо f₁=e₁ і f₂=e₂+αf₁, причому α підберемо так, щоб вектори f₁ і f₂ були ортогональними: (е₂+αf₁, f₁)=(e₂, f₁)+α(f₁, f₁)=0, звідки .

Оскільки 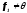, то знаменникІз лінійної незалежності векторівe₁=f₁ та e₂ випливає, що

Припустимо тепер, що попарно ортогональні ненульові вектори

f₁, f₂, …, f_k-1 вже знайдені. Покладемо

f_k=β₁f₁+β₂f₂+…+β_k-1f_k-1+e_k

і підберемо числа β₁, β₂, ..., β_k-1 так, щоб вектор f_k був ортогональним до f₁, f₂, …, f_k-1. Для цього потрібно, щоб виконувались рівності

(f_k, f_i)=β_i(f_i, f_i)+(e_k, f_i)=0

при і=1, 2, ..., k-1, звідки

.

Знаменник , оскільки всі векториза припущенням. Оскільки векторие₁, е₂, ..., е_k лінійно незалежні, то і отриманий вектор f_k теж буде ненульовим.

Такий процес продовжуватимемо доти, поки не знайдемо останнього ненульового вектора

f_n=γ₁f₁+γ₂f₂+…+γ_n-1f_n-1+e_n,

ортогонального до всіх попередніх векторів f₁, f₂, …, f_n-1. Згідно теореми 1 ортогональні вектори f₁, f₂, …, f_n лінійно незалежні і, отже, утворюють ортогональний базис. Якщо кожний із цих векторів поділити на його модуль, то отримаємо ортонормований базис, утворений векторами

▲

Спосіб доведення теореми є способом отримання ортонормованої системи векторів із заданої лінійно незалежної системи, який називають процесом ортогоналізації.

Якщо V₁ – підпростір V і е₁, е₂, ..., е_k – ортонормований базис V₁, то вектори е₁, е₂, ..., е_k можна включити в ортонормований базис всього простору V. Дійсно, достатньо доповнити систему векторів е₁, е₂, ..., е_k до базису простору V і здійснити ортогоналізацію отриманої множини векторів, починаючи із е₁, е₂, ..., е_k.

б) Скалярний добуток в координатах

Нехай е₁, е₂, ..., е_п – довільний базис евклідового простору V, х=х₁е₁+х₂е₂+...+х_пе_п, у=у₁е₁+у₂е₂+...+у_пе_п – два довільні вектори цього простору. Скориставшись властивостями скалярного добутку, знайдемо його вираження в координатах:

Якщо базис е₁, е₂, ..., е_п – ортонормований і х=х₁е₁+х₂е₂+...+х_пе_п, то, помноживши обидві частини останньої рівності скалярно на е_і, отримаємо, що (х,е_і)=х_і, тобто і-та координата вектора х в ортонормованому базисі дорівнює скалярному добутку вектора х на одиничний вектор е_і. Цей скалярний добуток називають проекцією вектора х на вектор е_і. Отже, координати вектора в ортонормованому базисі – це його проекції на базисні вектори.

в) Ортогональне доповнення

Два підпростори V₁ та V₂ евклідового простору V називаються взаємно ортогональними, якщо кожний вектор із V₁ ортогональний кожному вектору із V₂ (позначають V₁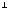V₂).

Приклад

У звичайному тривимірному просторі площина хОу та вісь Z є взаємно ортогональними підпросторами.

Площини хОу та уОz не є взаємно ортогональними підпросторами, оскільки не кожен вектор із хОz ортогональний довільному вектору із уОz.

Теорема 1. Для того, щоб підпростори V₁ та V₂ були взаємно

ортогональними, необхідно і достатньо, щоб всі базисні

вектори одного були ортогональні всім базисним

векторам другого.

Доведення.

Необхідність випливає із означення.

Для доведення достатності припустимо, що е₁, е₂, ..., е_k – базис V₁, f₁, f₂, …, f_m – базис V₂, причому (e_i, f_j)=0 для всіх i=1, 2,..., k, j=1, 2,…, m. Тоді для довільних та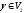

отже, ці вектори ортогональні. ▲

Теорема 2. Два взаємно ортогональних підпростори перетинаються

по нульовому вектору.

Доведення.

Якщо підпростори V₁ та V₂ взаємно ортогональні, то

тоді (х, х)=0, звідки х=θ. ▲

Нехай V₁ – довільний підпростір евклідового простору V. Виберемо в V₁ ортонормований базис е₁, е₂, ..., е_r і доповнимо його до ортонормованого базису е₁, е₂, ..., е_r, е_r+1,…, e_n всього простору V. Вектори е_r+1, …, e_n породжують (n-r)-вимірний простір V₂, ортогональний V₁. Підпростір V₂, утворений всеможливими векторами із V, ортогональними до всіх векторів із V₁, називається ортогональним доповненням V₁. Позначають його .

Теорема 3. Кожний вектор х із V, ортогональний V₁, належить

.

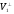Доведення.

Якщо вектор х=х₁е₁+х₂е₂+...+х_пе_п ортогональний V₁, то (х, е_і)=х_і=0 при і=1, 2, ..., r, звідки x=x_r+1e_r+1+…+x_ne_n. ▲

Ясно, що

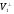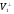Підпростори і породжують V і перетинаються по нульовому вектору. Значить, евклідів простір V являє собою пряму суму довільного свого підпростору і його ортогонального доповнення: . Тому кожний векторх із V можна однозначно подати у вигляді суми

x=y+z, де