mls94-complete[1]

6Summary

The following are the key concepts covered in this chapter:

1.The forward kinematics of a manipulator is described by a mapping gst : Q → SE(3) which describes the end-e ector configuration as a function of the robot joint variables. For open-chain manipulators consisting of revolute and prismatic joints, the kinematics can be written using the product of exponentials formula:

where ξi is the twist corresponding to the ith joint axis in the reference (θ = 0) configuration.

2.The (complete) workspace of a manipulator is the set of end-e ector configurations which can be reached by some choice of joint angles. The reachable workspace defines end-e ector positions which can be reached at some orientation. The dextrous workspace defines end-e ector positions which can be reached at any orientation.

3.The inverse kinematics of a manipulator describes the relationship between the end-e ector configuration and the joint angles which achieve that configuration. For many manipulators, we can find the inverse kinematics by making use of the following subproblems:

To find a complete solution, we apply the manipulator kinematics to a set of points which reduce the complete problem into an appropriate set of subproblems.

˙

4. The manipulator Jacobian relates the joint velocities θ to the end- e ector velocity Vst and the joint torques τ to the end-e ector wrench F :

If the manipulator kinematics is written using the product of exponentials formula, then the manipulator Jacobians have the form:

143

5.A configuration is singular if the manipulator Jacobian loses rank at that configuration. Examples for a general six degree of freedom arm include:

(a)Two collinear revolute joints

(b)Three parallel, coplanar revolute joint axes

(c)Four intersecting revolute joint axes

The manipulability of a robot provides a measure of the nearness to singularity.

6.A manipulator is kinematically redundant if it has more than the minimally required degrees of freedom. The self-motion manifold describes the set of joint values which can be used to achieve a desired configuration of the end-e ector. Internal motions correspond to motions along the self-motion manifold and satisfy

˙

Jst(θ)θ = 0.

7.A parallel manipulator has multiple kinematic chains connecting the base to the end-e ector. For the case of two chains, the kinematics satisfies the structure equation

where ξij is twist for the the jth joint on the ith chain. The Jacobian of the structure equation has the form

where Θi = (θi1, . . . , θini ). A kinematic singularity occurs when the dimension of the space of admissible forces drops rank. Other singularities can occur when the set of end-e ector forces which can be generated by the actuated joints drops rank.

7Bibliography

There is a vast literature on robot kinematics, including a number of textbooks devoted to analysis, design, and control of manipulators. For an introductory treatment of the topics presented here, consult the textbook by Craig [21]. See also [35, 36, 79, 90, 122]. The product of exponentials formula was initially described by Brockett [12]; the presentation given here was inspired by the dissertation of Paden [85]. A selection of advanced topics in the flavor of the tools presented in this section can be found in a collection of papers edited by Brockett [13].

144

In terms of bounds on the number of inverse kinematic solutions to a six degree of freedom manipulator, Rastegar, Roth and Scheinman [100] established a bound of 32 using a non-constructive proof. This bound was made constructive by Du y and Crane [29] and reduced to 16 by Primrose [94]. However, it was Lee and Liang [57] who gave a constructive procedure for finding the inverse kinematic solutions for a general manipulator. The procedure has been refined by Roth and Raghavan [96] and Manocha and Canny [64], whose account we follow in this chapter. Manseur and Doty [65] gave an example of a robot with 16 inverse kinematic solutions.

The treatment of parallel mechanisms given here is not the standard one. For a classical treatment of four-bar and other parallel mechanisms, see, for example, Hunt [42]. A detailed description of the four-bar synthesis problem, along with analytical and graphical solution techniques, can be found in the book by Erdman and Sandor [30], in addition to other textbooks on kinematics and design of mechanisms.

145

θ3

(iii) (iv)

Figure 3.23: Some simple three degree of freedom manipulators.

8Exercises

1.Draw the twists axes for the manipulators shown in Chapter 1.

2.Show that the forward kinematics map for a manipulator is independent of the order in which rotations and translations are performed.

3.For each of the three degree of freedom manipulators shown in Figure 3.23:

(a)Find the forward kinematics map.

(b)Solve the inverse kinematics problem using the Paden-Kahan subproblems.

(c)Derive the spatial and body Jacobians.

4.For each of the manipulators shown schematically in Figure 3.24:

(a)Find the forward kinematics map.

146

Figure 3.24: Sample manipulators. Revolute joints are represented by cylinders; prismatic joints are represented by rectangular boxes.

(b)Solve the inverse kinematics problem using the Paden-Kahan subproblems.

(c)Derive the spatial and body Jacobians.

(d)Give a geometric description of the singular configurations.

(e)Describe the reachable and dextrous workspaces and calculate the number of inverse kinematic solutions in di erent regions of the workspace.

(Note that some of these problems have already been solved in the examples.)

5.Subproblem 2′: Rotation about two non-intersecting axes

Solve Subproblem 2 when the two axes ξ1 and ξ2 do not intersect. Use this subproblem to solve the inverse kinematics for the elbow manipulator in Example 3.5 when the first two joints do not intersect at a point.

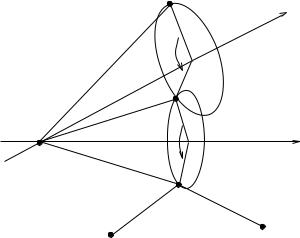
6.Subproblem 4: Rotation about two axes to given distances

Let ξ1, ξ2 be two zero-pitch unit magnitude twists with intersecting axes, and p, q1, and q2 be points in R3 (see Figure 3.25). Find θ1

and θ2 such that

b b

keξ1θ1 eξ2θ2 p − q1k = δ1

147

Figure 3.25: Subproblem 4: Rotate p about the axis of ξ1 followed by a rotation about the axis of ξ2 such that the final location of p is δ1 from q1 and δ2 from q2.

and

b b

keξ1θ1 eξ2θ2 p − q2k = δ2.

b b

(Hint: Find a point q such that q = eξ1θ1 eξ2θ2 p, and q is on the intersection of the three spheres centered at, respectively, q1, q2, and r, of radii δ1, δ2, and kp − rk.)

7. Subproblem 5: Translation to a given distance

Let ξ be an infinite-pitch unit-magnitude twist; p, q R3 two points; and δ a real number > 0. Find θ such that

b

kq − eξθ pk = δ.

Use this subproblem to solve for the extension of the prismatic joint in the SCARA robot in Example 3.6.

8.Show that the spatial velocity of a manipulator does not depend on the location of the tool frame (as long as it moves with the end-e ector).

9.Singular values of a matrix

Let A : Rn → Rp represent a linear map and assume that r is the

rank of A. Thus, r ≤ min(n, p). Show that there exist matrices U Rp×p, V Rn×n and Σ Rp×n such that

148

where

(a) The columns of V are orthonormal, i.e., V T V = I. Further, it may be partitioned as

V = v1 · · · vr vr+1 · · · vn = V1 V2

so that the range space of AT : Rp → Rn, denoted R(AT ), is spanned by the columns of V1, and the null space of A, denoted η(A), is spanned by the columns of V2.

(b) The columns of U are orthonormal, i.e., U T U = I, and it may be partitioned as

U = u1 · · · ur ur+1 · · · up = U1 U2

so that R(A) is spanned by the columns of U1, and η(AT ) is spanned by the columns of U2.

(c)Σ is a matrix of dimension p × n of the form

The σi are called the singular values of A, and Σ Rp×n is the representation of A in terms of the V basis for Rn and the

Ubasis for Rp.

10.Let J (θ) : Rn → R6 be the Jacobian of a manipulator. Show that

the manipulability measure µ3(θ) is given by the product of the singular values of J (θ); that is,

6

Y

µ3(θ) = σi(θ).

i=1

Thus, µ3(θ) is zero if and only if the Jacobian is singular.

11.Let A : Rn → Rp be of rank r and have singular value decomposition (3.74). Let B1 denote the ball of unit radius in Rn; that is,

B1 = {x Rn, kxk ≤ 1}.

Use the description of the matrices U, V of Exercise 9 to find the map under A of B1. Distinguish between the cases that p ≥ n and p ≤ n and also when r < min(n, p).

149

12.Let J (θ) : Rn → Rp be the Jacobian of a manipulator (p = 3 or 6). Assume that a task is modeled by an ellipsoid in the task space with its principal axes of length α1, · · · , αp. Let Eβ Rp be an ellipsoid of size scaled by β, namely

Define a manipulability measure on J (θ) which takes into account the task requirement as

µt(θ) := max{β : J (θ)(B1) Eβ }.

Characterize µt(θ) in terms of the singular values of J (θ) and lengths of the principal axes, α1, . . . , αp.

13.Isotropic points

A point in a manipulator’s workspace is said to be isotropic if the condition number of the Jacobian is 1.

(a)Calculate conditions under which a two-link planar manipulator has isotropic points and sketch their location in the plane.

(b)Compute the isotropic points for an elbow manipulator without a wrist.

(c)Discuss why isotropic points are useful for tasks which involve applying forces against the environment.

14.Euler angles can be used to represent rotations via the product of exponentials formula. If we think of (α, β, γ) as joints angles of a robot manipulator, then we can find the singularities of an Euler angle parameterization by calculating the Jacobian of the “forward kinematics,” where we are concerned only with the rotation portion of the forward kinematics map. Use this point of view to find singularities for the following classes of Euler angles:

(a)ZYZ Euler angles

(b)ZYX Euler angles

(c)XYZ Euler angles

15.Kinematic singularity: four coplanar revolute joints

Four revolute joint axes with twists ξi = (qi × ωi, ωi), i = 1, . . . , 4, are said to be coplanar if there exists a plane with unit normal n such that:

(a)Each axis direction is orthogonal to n: nT ωi = 0, i = 1, . . . , 4.

150

(b) The vector from qi to qj is orthogonal to n: nT (qi − qj ) = 0, i = 1, . . . , 4.

Show that when four of its revolute joint axes are coplanar, a six degree of freedom manipulator is at a singular configuration. Give an example of a manipulator exhibiting such a singularity.

16. Kinematic singularity: six revolute joints intersecting along a line

Six revolute joint axes with twists ξi = (qi × ωi, ωi), i = 1, . . . , 6, intersect along a line (p × n, n) if there exist constants γi, βi R, i = 1, ...6, such that

qi + γiωi = p + βin.

Show that when the six revolute joint axes of a six degree of freedom manipulator intersect along a line, the manipulator is at a singular configuration.

17.Kinematic singularity: prismatic joint perpendicular to two parallel coplanar revolute joints

A prismatic joint with twist ξ3 = (v3, 0) is normal to a plane containing two parallel revolute axes ξi = (qi × ωi, ωi), i = 1, 2, if

(a)v3T ωi = 0, i = 1, 2

(b)v3T (q1 − q2) = 0

(c)ω1 = ±ω2

Show that when this occurs, a six degree of freedom manipulator is at a singular configuration. Give an example of a manipulator exhibiting such a singularity.

18.In general, the manipulator Jacobian depends on the choice of base and tool frames. Determine which of the manipulability measures described in Section 4.4 is independent of the choice of base and/or tool frames.

19.Show that if a manipulator is at a singular configuration, then there exists an end-e ector wrench F which can be balanced without applying any joint torques. How is the wrench related to the twists which form the columns of the Jacobian?

20.Consider the slider-crank mechanism shown below:

151