mls94-complete[1]

3Force-Closure

An important property of a grasp is the ability to balance external object wrenches by applying appropriate finger wrenches at the contact points. For example, if we are using a multifingered hand to lift an object from a table, we must be able to exert forces on the object which act in the opposite direction to gravity. Depending on the task, we may also need to resist wrenches in other directions. Doing so is complicated by the fact that we must insure that the applied finger forces remain in the friction cone at all times so as to avoid slippage of the fingers on the surface of the object.

3.1Formal definition

If a grasp can resist any applied wrench, we say that such a grasp is force-closure.1 Formally, we make the following definition:

Definition 5.2. Force-closure grasp

A grasp is a force-closure grasp if given any external wrench Fe Rp applied to the object, there exist contact forces fc F C such that

Gfc = −Fe.

The following proposition follows directly from the definition.

Proposition 5.1. Characterization of all force-closure grasps

A grasp is force-closure if and only if G(F C) = Rp.

A key feature of a force-closure grasp is the existence of internal forces. An internal force is a set of contact forces which result in no net force on the object. In the previous (planar) example, we see that

0

1

fN = = GfN = 0.

0 1

This motivates the following definition. Let int(F C) denote the interior of the friction cone.

Definition 5.3. Internal forces

If fN N(G) ∩ F C, then fN is an internal force. If fN N(G) and fN int(F C), then it is called a strictly internal force.

1To be consistent with the literature, we use the term force-closure instead of wrench-closure.

223

Internal forces can be used to insure that contact forces satisfy friction cone constraints. Note that an internal force is a set of contact forces, represented with respect to the wrench basis at each contact. The following proposition shows that the existence of a strictly internal force is a necessary condition for a grasp to be force-closure.

Proposition 5.2. Necessity of internal forces

A grasp is force-closure if and only if G is surjective and there exists a vector of contact forces fN N(G) such that fN int(F C).

Proof. (Su ciency) Choose Fo Rp and let fc′ be any vector such that Fo = Gfc′. Since G is surjective, such an fc′ must exist. We will show that there exists an α such that fc′ + αfN int(F C). Notice that

therefore, there exists α′ su ciently large such that

fc′ + α′fN int(F C) F C. α′

From the properties of the friction cone, it follows that

fc := fc′ + α′fN int(F C)

and Gfc = Gfc′ = Fo.

(Necessity) Suppose that a grasp is force-closure. Choose f1 int(F C) such that Fo = Gf1 6= 0. Choose f2 F C such that Gf2 = −Fo

and define fN = f1 + f2. Then, we see that GfN = Fo − Fo = 0 and fN int(F C) from the properties of a cone.

3.2Constructive force-closure conditions

Verifying that a grasp is force-closure can be di cult due to the form of the friction cone. In certain simple cases, however, it is possible to verify that a grasp is force-closure directly from the definition. For example, if a grasp consists only of frictionless point contacts, then we saw that the grasp map had the form

F C = {f Rk : fi ≥ 0}.

Thus, G(F C) = R6 if and only if positive linear combinations of the columns of G span R6.

224

v2

v1

co(S) v3

v5

v6 v4

separating c hyperplane

Figure 5.7: Convex hull and separating hyperplane.

This example shows that the force-closure problem can be reformulated as a problem in positive linear spaces. This motivates the following set of definitions; see [97] for a more detailed introduction.

A set of vectors {v1, · · · , vk} with vi Rp is positively dependent if there exist αi > 0 such that

k

X

αivi = 0.

i=1

A set of vectors {v1, · · · , vk} positively spans Rn if for every x Rn there exists αi > 0, i = 1, · · · , k such that

k

X

αivi = x.

i=1

Any set of vectors which positively spans Rn is positively dependent (by choosing x = 0). Note that positively dependent vectors must have strictly positive coe cients: αi > 0.

A set K is said to be convex if for every x, y K, λx + (1 − λ)y K, λ [0, 1]. Thus any line connecting two points in a convex set lies in that set. The convex hull of a set S, denoted co(S), is the smallest convex set K containing S (i.e., it is the intersection of all convex sets containing S). Using these definitions, it can be shown that given a set S = {v1, · · · , vk}, the convex hull of S is

P P

co(S) = {v = αivi: αi = 1, αi ≥ 0}.

This concept is illustrated in Figure 5.7a.

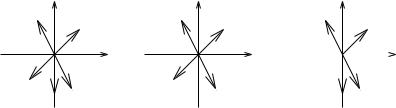
A useful object in the study of convex sets is the separating hyperplane. Given a point c Rp, we define a hyperplane through c with

225

normal v Rp as

Hv (c) = {x Rp : vT (x − c) = 0}.

It is a basic theorem in convex analysis that given any convex set K and a point c / K, there exists a hyperplane Hv (c) such that for all x K, vT (x − c) > 0. That is, all points in K lie on the “same side” of Hv (c). Such a hyperplane is called a separating hyperplane between K and c (see Figure 5.7b). If c lies on the boundary of K, then we replace the condition vT (x −c) > 0 by vT (x −c) ≥ 0 and we say Hv (c) is a supporting hyperplane.

The following proposition shows the utility of these concepts in determining if a grasp is force-closure.

Proposition 5.3. Convexity conditions for force-closure grasps

Consider a fixed contact grasp which contains only frictionless point contacts. Let G Rp×m be the associated grasp matrix and let {Gi} denote the columns of G. The following statements are equivalent:

1.The grasp is force-closure.

2.The columns of G positively span Rp.

3.The convex hull of {Gi} contains a neighborhood of the origin.

4.There does not exist a vector v Rp, v 6= 0, such that for i = 1, . . . , m, v · Gi ≥ 0.

The equivalence of conditions (1) and (2) follows from the definition of force-closure for a grasp with frictionless point contacts. The remaining conditions rely on tools from convexity theory which are beyond the scope of this book. See [97] for details.

The fourth condition of Proposition 5.3 is computationally attractive since candidates for v can be constructed from the columns of G. Namely, given any set of p − 1 independent columns of G, let v Rp be a nonzero vector which is perpendicular to the p −1 columns. To verify condition 4, we only need to check that the dot products of v and the remaining columns of G do not all have the same sign. It is left as an exercise to show that only values of v defined in this manner need to be considered. Note that the vector v, if it exists, defines the normal to a supporting hyperplane through the origin.

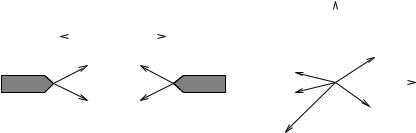
Example 5.4. Using convexity to determine force-closure

Consider the planar point contact grasps shown in Figure 5.8. In the first grasp, the contact locations are clustered near the corners of the rectangular object. The grasp map for these contacts is given by

226

Figure 5.8: Determining whether a planar grasp with point contacts is a force-closure grasp.

where a, b > 0. A supporting hyperplane candidate can be formed by choosing any two columns of G. Let vij represent the normal to the plane formed by Gi and Gj . Enumerating all possibilities, we have

Since none of these possibilities satisfy condition 4 of Proposition 5.3, we conclude the grasp is force-closure. The convex hull for this grasp is shown in the upper right of Figure 5.8.

For the second grasp, the contact points have been chosen such that

227

Figure 5.9: Force-closure for point contact with friction.

This grasp is not force-closure since it is not possible to resist torques using positive linear combinations of the columns of G (condition 2). The convex hull of the columns of G lies completely in the fx, fy plane, and does not include a neighborhood of the origin (condition 3). Finally, choosing v = (0, 0, 1),

vT G = 0 0 0 0 ,

and hence condition 4 also fails.

In some cases, the results of Proposition 5.3 can be extended to grasps which include frictional contacts. We motivate this with an example:

Example 5.5. Using convexity for grasps with friction

Consider the planar grasp shown in Figure 5.9. Rather than describe this grasp using our usual contact wrench basis, we note that all contact forces which lie in the friction cone can be written as positive linear combinations of the forces which describe the edges of the cone. Hence, we can determine if a grasp is force-closure by checking to see if the object wrenches corresponding to the edges of the contact friction cone positively span the object wrench space.

In the case of planar contacts, this is equivalent to defining a contact

which has the same form as two independent, frictionless point contacts. Hence, by appropriate choice of basis, we can use Proposition 5.3 to check force-closure of planar grasps with friction.

228

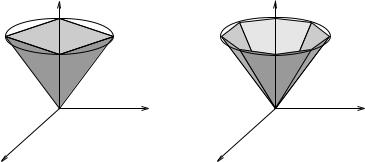
Figure 5.10: Approximations of a spatial friction cone.

For spatial (3-D) grasps, the extension of Proposition 5.3 to contact models with friction is not so straightforward. Since the friction cone cannot be represented as the sum of a finite set of vectors, we cannot use the convex hull of a finite basis to determine if a grasp is forceclosure. In practice, the circular friction cone can be approximated by a cone generated by a finite set of vectors. This situation is shown in Figure 5.10. The force-closure condition can then be checked by evaluating the convex hull of the (conservative) approximation. If the convex hull contains a neighborhood of the origin, then the grasp is force-closure. For a finite-dimensional approximation, this is a su cient but not necessary condition.

Additional methods of checking force-closure for spatial grasps are given in the next section.

4Grasp Planning

In this section, we briefly present methods for choosing contact locations which result in a force-closure grasp.

4.1Bounds on number of required contacts

Suppose that we are given the task of designing a multifingered robot hand for use in a given set of tasks. One of the first decisions that must be made is the number and type of the fingers. In this section, we consider the following question: given a contact model, how many fingers are necessary to grasp any object? This places a lower bound on the number of fingers which we must include on our hand, given a choice of contact type.

Given an object O R3 (or O R2 for the planar case), let Σ = ∂O denote the boundary of the object. We assume that Σ is a connected,

229

Table 5.3: Lower bounds on the number of fingers required to grasp an object.

grasp is force-closure, then 0 int(S) and by Steinitz’s theorem there exist 2p vectors v1, . . . , v2p Λ(Σ) which generate a force-closure grasp. Hence, Steinitz’s theorem guarantees that we need at most 2p contacts to grasp any non-exceptional object. These 2p vectors may not be unique; Figures 5.11b and 5.11c show two choices of 4 vectors which span R2. Note that in Figure 5.11c, v3 is redundant, but in Figure 5.11b all of the vectors are needed to positively span R2.

Caratheodory’s and Steinitz’s theorems allow us to bound the number of contacts required for a force-closure grasp using frictionless point contacts. If we let p be the dimension of the wrench space and k be the number of contacts, then

It can be shown that for the planar case (p = 3) the lower bound is achievable for all non-exceptional surfaces. For the spatial case (p = 6), proofs exist for special classes of objects showing that the lower bound can be achieved, but the general case is not completely solved. Among the more useful classes of objects which can be grasped with at most seven contacts are the set of polyhedral objects and the set of everywhere smooth objects.

For more general contact types, bounds on the number of contacts are also available. A detailed description of these bounds is beyond the scope of this book, but can be found in [66]. We note that for the point contact with friction case, the lower bounds can be exhibited using a regular tetrahedron (or equilateral triangle in the plane) and choosing µ < tan 19.5◦. This issue is explored further in the exercises and in the next section.

Table 5.3 summarizes the number of contacts required for various contact models. These bounds are lower bounds on the number of contacts required for a force-closure grasp of any object in the indicated class. That is, in order to be able to grasp every object in the class, at least that many contacts must be available.

231

n2

Figure 5.12: Geometric relationships for 2-D force-closure grasp using two point contacts with friction.

4.2Constructing force-closure grasps

In this section, we show one particularly simple method of computing and constructing force-closure grasps for the case of two point contacts with friction and a planar object. The algorithm is based on the following theorem:

Theorem 5.6. Planar antipodal grasps [82]

A planar grasp with two point contacts with friction is force-closure if and only if the line connecting the contact point lies inside both friction cones.

A grasp satisfying the conditions of this theorem is called an antipodal grasp. The proof of the theorem is left as an exercise.

To convert this theorem into an algorithm for planning grasps, we note that the conditions of the theorem can be written as a set of linear inequality constraints. Let n1 denote the inward pointing normal at the contact point p1 and n2 denote the inward point normal at the contact point p2 (see Figure 5.12). Given a unit vector n, define n to be the unit vector perpendicular to n which satisfies

n n = +1,

where is the 2-D cross product:

a b = det[a b] a, b R2.

Suppose that we are given a polygonal object and we wish to find all possible force-closure grasps. The constraints that the line between contacts lie in the relevant friction cones become:

A : (n1 − µn1 ) (p2 − p1) > 0 B : (n1 + µn1 ) (p2 − p1) < 0 C : (n2 − µn2 ) (p1 − p2) > 0 D : (n2 + µn2 ) (p1 − p2) < 0.

232