
mls94-complete[1]
.pdf
where Σ(c3, s3) R6×9.
If the rank of Q is an integer k less than 8, then one can only solve for k of the variables s1s2, s1c2, c1s2, s1, c1, s2, c2 and we are left with six equations in 9 + 8 − k variables in place of (3.48). We will not describe the algorithm in detail for this scenario, for details we refer the reader to [64].
Step 6. We will assume that Q has rank 8, so that the equation of (3.48) holds. To make the equations (3.48) polynomial rather than trigonometric, use the substitutions
si = |
2xi |
ci = |
1 − xi2 |
|
1 + x2 |
1 + x2 |
|||
|
|
|||
|
i |
|
i |
Use this in equation (3.48) and multiply each equation by (1 + x24) and
(1 + x2) to clear the denominators. Now, multiply the first four equations |
||||||||
5 |
|
|
|
|
|
|
|
|
by (1 + x2) to get |
|
|
|
|
|
|
|
|
3 |
|
|
|
x42x52 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
x42x5 |
|
|
|||
Σ |
(x |
) |
x42 |
|
= 0. |
(3.49) |
||
|
x x2 |
|
||||||
1 |
3 |
|
|
4 |
5 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x4 2 |
5 |
|
|
||
|
|
|
|
x5 |
|
|
|
|
|
|
|
|
x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Step 7. We now use dialytic elimination to eliminate x4, x5 as in the previous example by multiplying the six equations in equation (3.49) by x4 and then appending them to the original set to get 12 equations of the
form |
|
|
|
x43 |
|
|
|
|
|
|
|
|
|
x43x52 |
|
|
|
|
|
|
|
|
x43x5 |
|
|
|
|
|
Σ (x ) |
0 |
x42x5 |
|
|
||
|
|
0 |
Σ1(x3) |
|
x4 |
|
|
|
|
|
|
|
|
x42x52 |
|
|
|
|
|
|
|
x4x52 |
|
|
||
Σ¯ := 1 3 |
|
x4x5 |
|
|
|
|||
|
|
x4 |
|
= 0. |
(3.50) |
|||
|
|
2 |
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
x5 |
|
|
|
|
|
|
|
|
x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯
Step 8. The polynomial equation det Σ = 0 is a polynomial of order 16 in x3. Once we solve for x3, we solve for x4, x5 from the determination of
¯
the null space of Σ as in the Example 3.4. Then, we solve for θ1, θ2 from equation (3.47). This yields the solutions to all the angles except θ6. For this purpose, we return to the form of the kinematics
gst(θ) = eb1 |
θ |
1 · · · eb6 |
θ |
6 gst(0) = gd, |
ξ |
ξ |
|
with all the variables known except θ6. By choosing any point p, we may
write this equation as |
6 p = e−b5 |
|
5 · · · e−b1 |
|
1 gdgst− |
|
|
eb6 |
θ |
θ |
θ |
p =: q |
|||
ξ |
ξ |
ξ |
1 |
|
|||
Now we use Subproblem 1 from the preceding subsection to solve for θ6.
Number of inverse kinematics solutions
The set of steps outlined above results in a 16th order polynomial for x3 and hence θ3. This polynomial may or may not have 16 real roots. In the instance of the elbow manipulator, we saw that the maximum number of feasible solutions was eight. One may verify that if the three wrist axes of the elbow manipulator do not intersect at a point, the number of inverse kinematics solutions for this manipulator may be as high as 16. Indeed, 16 is the upper bound of number of solutions of any open-link spatial mechanism with six degrees of freedom. This number is a sharp bound—that is to say, it is achievable (see, for example, [65])—and is far superior to those obtained from a brute force elimination technique using Bezout’s theorem. Indeed, this bound of 16 is a tribute to the ingenuity of Lee and Liang [57] who were the first to notice the set of tricks presented above and put to rest a number of erroneous conjectures that had been populating the literature up to that point. Not the least of their tricks is the rewriting of the kinematic equations as equation (3.43).
The algorithm as stated above has some drawbacks, as pointed out by Manocha and Canny [64]. The majority of the drawbacks are numerical, owing to the computation of determinants of ill-conditioned matrices, though there are some conceptual ones as well. For an example of a conceptual drawback, we have the modification of the procedure in Step 5 above for choosing fewer than eight independent equations out of 14 to eliminate as many of the cosines and sines of θ1, θ2 when the rank of the matrix Q is less than 8 to produce an over determined set of equations. The aforementioned paper shows that a general computational technique of converting the dialytical elimination technique into a generalized eigenvalue problem can be brought to bear on the inverse kinematics problem so as to improve its numerical conditioning and speed of computation. These computational details are of tremendous importance when realtime computation of the inverse kinematics solutions needs to be done in the context of obstacle avoidance for robots in cluttered environments.
114
4The Manipulator Jacobian
In addition to the relationship between the joint angles and the end- e ector configuration, one often makes use of the relationship between the joint and end-e ector velocities. In this section, we derive a formula for this relationship and study its structure and properties. We also study the dual relationship between end-e ector wrenches and joint torques.
Traditionally, one describes the Jacobian for a manipulator by differentiating the forward kinematics map. This works when the forward kinematics is represented as a mapping g : Rn → Rp, in which case the Jacobian is the linear map ∂g∂θ (θ) : Rn → Rp. However, if we represent the forward kinematics more completely as g : Rn → SE(3), the Jacobian is not so easily obtained. The problem is that ∂g∂θ (θ) is not a natural quantity since g is a matrix-valued function. Of course, one could always choose coordinates for SE(3), but this description only holds locally. More importantly, choosing a local parameterization for SE(3) destroys the natural geometric structure of rigid body motion.
To correct this problem, we use the tools of Chapter 2 to write the Jacobian of the forward kinematics map in terms of twists. We shall see that the product of exponentials formula leads to a very natural and explicit description of the manipulator Jacobian, which highlights the geometry of the mechanism and has none of the drawbacks of a local representation.
4.1End-e ector velocity
Let gst : Q → SE(3) be the forward kinematics map for a manipulator. If the joints move along a path θ(t) Q, then the end-e ector traverses a path gst(θ(t)) SE(3). The instantaneous spatial velocity of the end- e ector is given by the twist
|
|
|
|
|
V s |
= g˙ |
|
(θ)g−1 |
(θ). |
|
|
||
Applying the chain rule, |
bst |
|
st |
|
st |
|
|
|
|
||||
b |
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
X |
∂gst |
|
|
|
|
|
X |
|
∂gst |
|
|
|
Vsts |
= |
i=1 |
∂θi |
θ˙i |
gst−1(θ) = |
i=1 |
∂θi |
gst−1(θ) θ˙i, |
(3.51) |
||||
and we see that the end-e ector velocity is linearly related to the velocity of the individual joints. In twist coordinates, equation (3.51) can be written as
|
|
|
s |
|
|
|
s |
˙ |
|
|
|
|
|
|
|
|
|
Vst |
= Jst(θ)θ, |
|
|
|
|
|
|
||||
where |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
s |
∂gst |
|
|
|
∂gst |
|
||||||||
Jst(θ) = |
|
gst−1 |
|
· · · |
|
gst−1 |
|
(3.52) |
||||||
∂θ1 |
|
∂θn |
|
|||||||||||
115
We call the matrix Jsts (θ) R6×n the spatial manipulator Jacobian. At each configuration θ, it maps the joint velocity vector into the corresponding velocity of the end-e ector.
If we represent the forward kinematics using the product of exponentials formula, we can obtain a more explicit and elegant formula for Jsts . Let
|
|
|
|
|
|
|
|
gst(θ) = eb1 |
|
1 |
· · · eb |
|
|
|
gst(0) |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
θ |
|
|
|
ξn θn |
|
|
|
|
|
|
|
|
|
||||
represent the mapping g |
|
: Q |
→ |
SE(3), where ξ |
|
|
se(3) are unit twists. |
|||||||||||||||||||||||||
Then, |
gst− |
= eb1 |
|
|
|
|
st |
|
|
|
|
|
|
eb |
|
|
|
|
|
bi |
|
|
|
|
|
|||||||
∂θi |
1 · · · eb −1 |
|
|
−1 |
∂θi |
|
eb +1 |
|
+1 · · · eb |
gst(0) gst− |
||||||||||||||||||||||
|
∂gst |
1 |
ξ θ |
|
|
|
|
ξi |
|
θi |
|
∂ |
|
|
ξi θi |
|
|
ξi θi |
|
|
ξn θn |
1 |
||||||||||
|
|
|
= eb1 |
1 · · · eb −1 |
|
|
−1 |
ξi |
|
eb |
|
|
· · · eb |
|
|
gst(0) gst− |
|
|||||||||||||||
|
|
|
ξ θ |
|
|
· · · |
|
b |
|
θi |
|
bi |
|
ξi θi |
|
|
|
|
· · · |
|
|
|
1 |
|
||||||||
|
|
|
|
|
|
|
ξi |
|
|
|
|
|
|
|
|
ξn θn |
|
|
|
|
||||||||||||
|
|
|
= eξ1θ1 |
|
|
eξi−1θi−1 ξ |
e−ξi−1θi−1 |
|
|
|
e−ξ1θ1 |
|
||||||||||||||||||||
|
|
|
b |
|
|
|
|
coordinates, |
|
b |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|||||||||
and, converting to twist |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
∂gst |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
gst−1 |
|
= Ad eξ1θ1 |
|
|
|
eξi−1θi−1 |
|
ξi. |
(3.53) |
|||||||||||||||||
|
|
|
∂θi |
|
|
· · · |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
b |
|
|
|
|
|
|
|
||||
The spatial manipulator Jacobian becomes |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
Jsts (θ) = ξ1 |
|
|
ξ2′ |
|
· · · |
|
|
ξn′ |
|
|
|
|
|
(3.54) |
||||||||||
|
|
|
|
|
|
|
|
ξi′ = Ad |
|
eb1 |
θ |
1 |
· · · eb |
−1 |
θ |
i−1 |
ξi |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
|
|
ξi |
|
|
|
|
|
|
|
|
|
|
||||
Jsts (θ) : Rn → R6 is a configuration-dependent matrix which maps joint velocities to end-e ector velocities.
Equation (3.54) shows that the manipulator Jacobian has a very special structure. By virtue of the definition of ξ′, the ith column of the Jacobian depends only on θ1, . . . , θi−1. In other words, the contribution of the ith joint velocity to the end-e ector velocity is independent of the configuration of later joints in the chain. Furthermore, the ith column of the Jacobian,
ξi′ = Ad |
ξ |
θ |
1 |
|
ξi |
θi |
−1 |
ξi, |
|
eb1 |
|
· · · eb −1 |
|
|
|||
corresponds to the ith joint twist, |
ξ , |
transformed by the rigid trans- |
||||||
|
|
|
|
i |
|
|
|
|
formation exp(ξ1θ1) · · · exp(ξi−1θi−1). |
This is precisely the rigid body |
|||||||
b b
transformation which takes the ith joint frame from its reference configuration to the current configuration of the manipulator. Thus, the ith column of the spatial Jacobian is the ith joint twist, transformed to the current manipulator configuration. This powerful structural property means that we can calculate Jsts (θ) “by inspection,” as we shall see shortly in an example.
116

It is also possible to define a body manipulator Jacobian, Jstb , which is defined by the relationship
b b ˙
Vst = Jst(θ)θ.
A calculation similar to that performed previously yields
Jstb (θ) = ξ1†
ξi† = Ad−1b
eξi θi
· · · ξn†−1 ξn†
(3.55)
bξi
·· · eξn θn gst(0)
The columns of Jstb correspond to the joint twists written with respect to the tool frame at the current configuration. Note that gst(0) appears explicitly; choosing S such that gst(0) = I simplifies the calculation of Jstb . The spatial and body Jacobians are related by an adjoint transformation:
Jsts (θ) = Adgst(θ) Jstb (θ). |
(3.56) |
The spatial and body manipulator Jacobians can be used to compute the instantaneous velocity of a point attached to the end-e ector. Let qb represent a point attached to the end-e ector, written in body (tool) coordinates. The velocity of qb, also in body coordinates, is given by
b b b b b ˙ b
vq = Vstq = Jst(θ)θ q .
Similarly, if we represent our point relative to the spatial (base) frame,
then s b s s s ˙ s vq = Vstq = Jst(θ)θ q .
If we desire the velocity of the origin of the tool frame, then qb = 0 but qs = gst(θ)qb = p(θ), the position component of the forward kinematics map. Thus, using homogeneous coordinates explicitly,
vqs = |
0 |
= RstVstb |
1 |
= Vsts |
1 |
|
p˙(θ) |
b |
0 |
b |
p(θ) |
|
|
|
|
are all equivalent expressions for the velocity of the origin of the tool frame.
The relationship between joint velocity and end-e ector velocity can be used to move a robot manipulator from one end-e ector configuration to another without calculating the inverse kinematics for the manipulator. If Jst is invertible, then we can write
θ˙(t) = (Jsts (θ))−1Vsts (t). |
(3.57) |
117

θ2 |
θ3 |
|
|
l2 |
θ1 |
|
l1 |
θ4 |
|
T
S  l0
l0
Figure 3.13: SCARA manipulator in non-reference configuration.
If Vsts (t) is known, equation (3.57) is an ordinary di erential equation for θ. To move the end-e ector between two configurations g1 and g2, we pick any workspace path g(t) with g(0) = g1 and g(T ) = g2, calculate
the spatial velocity V s |
= gg˙ −1, and integrate equation (3.57) over the |
|
interval [0, T ]. |
b |
|
Example 3.8. Jacobian for a SCARA robot
Consider the SCARA robot at an arbitrary configuration θ Q, as shown in Figure 3.13. The spatial Jacobian can be evaluated by writing the twists associated with each joint in its current configuration. For the SCARA, the directions of the twists are fixed and only the points through which the axes of the twists pass are functions of θ. By inspection,
q1′ = |
0 |
q2′ = |
−l1 cos θ1 |
|
q3′ |
= |
−l1 cos θ1 + l2 cos(θ1 |
+ θ2) |
|
||||
|
0 |
|
|
|
l1 sin θ1 |
|
|
|
l1 sin θ1 − l2 sin(θ1 |
+ θ2) |
|||
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
||
are points on the axes. Calculating the associated twists yields |
|
|
|||||||||||
|
|
|
0 |
l1 sin θ1 |
l1 sin θ1 |
+ l2 sin(θ1 |
+ θ2) |
0 |
|
|
|||
|
|
Jsts = |
0 |
l1 cos θ1 |
l1 cos θ1 |
+ l2 cos(θ1 |
+ θ2) |
0 |
|
|
|||
|
|
0 |
|
0 |
|
|
|
0 |
|
0 . |
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
||
|
|
|
0 |
|
0 |
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
As a check, one can calculate the linear velocity of the end-e ector using
s ˙
the formula (Jstθ) p(θ) and verify that it agrees with p˙(θ).
118
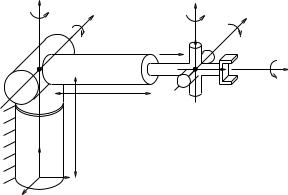
ξ1 |
ξ4 |
|
ξ2 |
||
ξ5 |
||
|
ξ3 |
|
q1 |
ξ6 |
|
|
qw |
|
l1 |
|
|
l0 |
|
|
S |
|
Figure 3.14: An idealized version of the Stanford arm.
Example 3.9. Jacobian for the Stanford arm
The Stanford arm, shown in Figure 3.14, is a six degree of freedom robot with two revolute joints at the base, a prismatic joint, and a spherical wrist. It is very similar to an elbow manipulator, with the “elbow” replaced by a prismatic joint.
The spatial manipulator Jacobian for the Stanford arm is computed by determining the location and directions of the joint twists as a function of the joint angles. For example, the first two joints pass through the point q1 = q2 = (0, 0, l0) and point in the directions ω1 = (0, 0, 1) and ω2′ = (− cos θ1, − sin θ1, 0). This gives joint twists
ξ1 = |
− |
× |
|
= |
|
0 |
|
ξ2′ |
= − |
|
× |
|
= |
cos θ1 |
. |
|
ω1 |
|
|
0 |
|
|
ω′ |
|
|
l0 sin θ1 |
|
||||
|
ω1 |
q1 |
|
|
|
0 |
|
|
|
ω′ |
|
q1 |
|
−l0 cos θ1 |
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
− 0 |
||
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|||
|
|
|
|
0 |
|
|
|
2 |
|
− sin θ1 |
|
||||
The third joint is prismatic and hence we care only about its direction. Taking into account the change in orientation due to the first two joints, we have
ξ3′ = |
b b |
h |
0 |
= |
− 0 |
2 |
= |
0 |
|
" |
0 |
i# |
|
0 |
|
|
|
||
|
ezθ1 e−xθ2 |
|
0 |
|
− sin θ1 cos θ2 |
|
v′ |
|
|
|
|
1 |
|
cos θ1 cos θ2 |
|
|
|||
|
|
|
|
0 |
|
3 |
|
||
|
|
|
|
|
sin θ |
|
|
|
|
Finally, we compute the twists corresponding to the wrist. located at the point
.
The wrist is
qw′ = |
|
0 |
+ e |
θ1 e− |
θ2 |
l1 |
+ θ3 |
= |
(l1 |
+ θ3) cos θ1 cos θ2 |
. |
|||
|
|
0 |
|
z |
|
x |
|
|
0 |
|
|
−(l1 + θ3) sin θ1 cos θ2 |
|
|
|
l0 |
|
b |
b |
|
|
0 |
|
|
l0 |
− (l1 + θ3) sin θ2 |
|
||
|
|
|
|
|
||||||||||
119

The directions of the wrist axes depend on θ1 and θ2 as well as the preceding wrist axes. These are given by
ω4′
ω5′
ω6′
|
|
|
0−s1s2
=ebzθ1 e−xbθ2 0 = c1s2
|
|
|
1 |
|
|
|
c2 |
|
|
|
|
|
z |
|
x |
z |
|
−1 |
= |
−c1c4 + s1c2s4 |
|||||
= e |
θ1 e− |
θ2 e θ4 |
0 |
− |
s1c4 |
− |
c1c2s4 |
|||||
b |
b |
b |
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
s2s4 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0−c5(s1c2c4 + c1s4) + s1s2s5
=ebzθ1 e−xbθ2 ebzθ4 e−xbθ5 1 = c5(c1c2c4 − s1s4) − c1s2s5
0−s2c4c5 − c2s5
.
Combining these directions with our calculations for qw′ , we can now write the complete manipulator Jacobian:
st |
ω1 |
− |
ω2′ |
0 |
ω4′ |
ω5′ |
ω6′ |
|
J s = |
0 |
|
ω2′ × q1 |
v3′ |
−ω4′ × qw′ |
−ω5′ × qw′ |
−ω6′ × qw′ |
, |
(3.58)
where the various quantities are defined above.
Note that we were able to calculate the entire manipulator Jacobian without explicitly di erentiating the forward kinematics map.
As a final comment, we re-emphasize that the manipulator Jacobian di ers from the Jacobian of a mapping f : Rn → Rp. For instance, in Example 3.8 (the SCARA manipulator), it is possible to define the configuration of the end-e ector as x = (p(θ), φ(θ)), where p(θ) is the xyz position of the tool frame and φ(θ) = θ1 + θ2 + θ3 is the angle of rotation of the tool frame about the z-axis. The kinematics is then represented by the mapping x = f (θ) and by the chain rule
∂f ˙ x˙ = ∂θ θ.
The matrix ∂f∂θ is the Jacobian of the mapping f : Q → R4, but it is not the manipulator Jacobian (body or spatial). In particular, the columns of cannot be interpreted as the instantaneous twist axes corresponding
to each joint.
Similarly, for a general manipulator, one can choose a local parameterization for SE(3) and write the kinematics as f : Q → R6. Once again, the Jacobian of the mapping f : Q → R6 has no direct geometric interpretation, even though it has the same dimensions as the manipulator Jacobian. Furthermore, for manipulators which generate full rotation of the end-e ector, the parameterization of SE(3) by a vector of six numbers introduces singularities which are solely an artifact of the parameterization. These singularities may lead to false conclusions about the ability
120
of the manipulator to reach certain configurations or achieve certain velocities. The use of the manipulator Jacobian, as we have defined it here, avoids these di culties.
4.2End-e ector forces
The manipulator Jacobian can also be used to describe the relationship between wrenches applied at the end-e ector and joint torques. This relationship is fundamental in understanding how to program robots to interact with their environment by application of forces. We shall see that the duality of wrenches and twists discussed in Chapter 2 extends to manipulator kinematics.
To derive the relationship between wrenches and torques, we calculate the work associated with applying a wrench through a displacement of the end-e ector. If we let gst(θ(t)) represent the motion of the end-e ector, the net work performed by applying a (body) wrench Ft over an interval
of time [t1, t2] is Z t2
W = Vstb · Ft dt,
t1
where Vstb is the body velocity of the end-e ector. The work will be the same as that performed by the joints (assuming no friction), and hence
Zt1 |
θ˙ · τ dt = W = Zt1 |
Vstb · Ft dt. |
t2 |
t2 |
|
Since this relationship must hold for any choice of time interval, the integrands must be equal. Using the manipulator Jacobian to relate Vstb
˙
to θ, we have
˙T |
˙T |
b T |
|
θ |
τ = θ |
(Jst) Ft. |
|
˙ |
|
|
|
It follows that since θ is free, |
|
|
|
|
τ = (Jstb )T Ft. |
(3.59) |
|
This equation relates the end-e ector wrench to the joint torques by giving the torques that are equivalent to a (body) wrench applied at the end-e ector.
A similar analysis can be used to derive the relationship between a spatial wrench Fs applied at the end-e ector and the corresponding joint torques:
τ = (Jsts )T Fs. |
(3.60) |
The full derivation of this equation is left as an exercise.
The interpretation of the Jacobian transpose as a mapping from end- e ector forces to joint torques must be made carefully. If the Jacobian is square and full rank, there are no di culties. However, in all other
121
cases, the relationship can be misleading. We defer the discussion of singularities to the next section, and consider only the case when Jst is not square.
The formulas given by equations (3.59) and (3.60) describe the force relationship that must hold between the end-e ector forces and joint torques. We can use these equations to ask two separate questions:
1.If we apply an end-e ector force, what joint torques are required to resist that force?
2.If we apply a set of joint torques, what is the resulting end-e ector wrench (assuming that the wrench is resisted by some external agent)?
Equation (3.59) answers the first question in all cases. However, in manipulation tasks, we are often more interested in answering the second question, which can be recast as: what joint torques must be applied to generate a given end-e ector wrench?
If the number of joints is larger than the dimension of the workspace, then we say the manipulator is kinematically redundant. In this case, we can generically find a vector of joint torques which generates the appropriate end-e ector force, as given by equation (3.59). However, since there are more joints than the minimum number required, internal motions may exist which allow the manipulator to move while keeping the position of the end-e ector fixed. Redundant manipulators are discussed in more detail in Section 5.
If, on the other hand, the number of joints is smaller than the dimension of the workspace, then there may be no torque which satisfies equation (3.59) for arbitrary end-e ector wrenches, and therefore some end-e ector wrenches cannot be applied. They can, however, be resisted by the manipulator. This is a consequence of our assumption that the allowable motion of the manipulator is completely parameterized by the joint angles θ. If a wrench causes no joint torques, it must be resisted by structural forces generated by the mechanism. Such a situation occurs when F lies in the null space of JstT . In this case, the force balance equation is satisfied with τ = 0; the resisting forces are supplied completely by the robot’s mechanical structure.
Example 3.10. End-e ector forces for a SCARA robot
Consider again the SCARA robot from the Example 3.8. The transpose of the spatial manipulator Jacobian is
(Jsts )T = |
|
|
l1c1 |
|
|
|
l1s1 |
|
0 |
0 |
0 |
1 . |
|
|
|
|
0 |
|
|
|
0 |
|
0 |
0 |
0 |
1 |
|
1 |
1 |
0 2 |
12 |
1 |
1 |
0 2 |
12 |
1 |
0 |
0 |
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l c + l c |
|
l s + l s |
|
0 |
0 |
0 |
1 |
|
||||
|
|
|
|
||||||||||
122
