
mls94-complete[1]
.pdf
8Exercises
1.Let a, b, c R3 be 3-vectors and let · and × denote the dot product and cross product in R3. Verify the following identities:
(a)a · (b × c) = (a × b) · c
(b)a × (b × c) = (a · c)b − (a · b)c
2.Using the homogeneous representation, show that SE(3) satisfies the axioms of a group, with the group multiplication given by the usual matrix multiplication.
3.Properties of rotation matrices
Let R SO(3) be a rotation matrix generated by rotating about a unit vector ω by θ radians. That is, R satisfies R = exp(ωθb ).
(a)Show that the eigenvalues of ωb are 0, i, and −i, where i =
√
−1. What are the corresponding eigenvectors?
(b)Show that the eigenvalues of R are 1, eiθ , and e−iθ . What is the eigenvector whose eigenvalue is 1?
(c) Let R = r1 r2 r3 be a rotation matrix. Show that det R = r1T (r2 × r3).
4.Properties of skew-symmetric matrices
Show that the following properties of skew-symmetric matrices are true:
(a)If R SO(3) and ω R3, then RωRb T = (Rω) .
(b)If R SO(3) and v, w R3, then R(v × w) = (Rv) × (Rw).
(c)Show that so(3) is a vector space. Determine its dimension and give a basis for so(3).
5.Cayley parameters
Another parameterization of SO(3), which does not involve transcendental functions, is Cayley’s parameterization. Let a be a vector in R3 and let ba be the associated 3 × 3 skew-symmetric matrix.
(a)Show that Ra = (I − ba)−1(I + ba) SO(3).
(b)Verify that
|
1 |
2 |
1 |
2 |
3 |
2 |
2 |
2 |
|
3 |
||
|
|
|
1+a2 |
−a2 |
−a2 |
2(a1a2 |
− a3) |
|
2(a1a3 + a2) |
|
||
Ra = |
|
4 |
2(a1a2 + a3) |
1−a1 +a2 − a3 |
2(a2a3 − a1) |
5 |
||||||
1+kak2 |
||||||||||||
|
2(a1a3 − a2) |
|
2(a2a3 + a1) 1−a12 −a22 +a32 |
|||||||||
(c) Given a rotation matrix R, compute the Cayley parameters a.
73

6. Unit quaternions
Let Q = (q0, ~q ) and P = (p0, p~ ) be quaternions, where q0, p0 R are the scalar parts of Q and P and ~q, p~ are the vector parts.
(a)Show that the set of unit quaternions satisfies the axioms of a group.
(b)Let x be a point and let X be a quaternion whose scalar part is zero and whose vector part is equal to x (such a quaternion is
called a pure quaternion). Show that if Q is a unit quaternion, the product QXQ is a pure quaternion and the vector part
of QXQ satisfies
(q02 − ~q · ~q )~x + 2 q0(~q × ~x ) + (x · ~q )~q .
Verify that the vector part describes the point to which x is rotated under the rotation associated with Q.
(c)Show that the set of unit quaternions is a two-to-one covering of SO(3). That is, for each R SO(3), there exist two distinct unit quaternions which can be used to represent this rotation.
(d)Compare the number of additions and multiplications needed to perform the following operations:
i.Compose two rotation matrices.
ii.Compose two quaternions.
iii.Apply a rotation matrix to a vector.
iv.Apply a quaternion to a vector [as in part (b)].
Count a subtraction as an addition, and a division as a multiplication.
(e)Show that a rigid body rotating at unit velocity about a unit vector in ω R3 can be represented by the quaternion di erential equations
˙ ·
Q Q = (0, ω/2),
where · represents quaternion multiplication.
7.A rigid body moving in R2 has three degrees of freedom (two components of translation and one of rotation), a rigid body moving in R3 has six degrees of freedom (three each of translation and rota-
tion). Show that a rigid body moving in Rn will have 12 (n + n2) degrees of freedom. How many are translational and how many are rotational?
8.Properties of the matrix exponential
Let Λ be a matrix in Rn×n. The exponential of Λ is defined as
eΛ = I + Λ + Λ2 + Λ3 + · · ·
2! 3!
74
(a)Choose a matrix norm and show that the above series converges.
(b)Let g Rn×n be an invertible matrix. Show the following equality:
|
|
|
geΛg−1 = egΛg−1 . |
|
|||
(c) Verify that |
|
|
|
|
|
||
|
d |
Λθ |
˙ |
Λθ |
Λθ |
˙ |
|
|
dt |
e |
|
= (Λθ)e |
= e |
(Λθ). |
|
9.Projection maps and proof of Proposition 2.9
This problem completes the proof of Proposition 2.9 using the properties of projection maps on linear spaces. Assume ω so(3) and kωk = 1.
(a)Given a vector ω R3, let Nω denote the subspace spanned by ω and Nω denote the orthogonal complement. Show that
image ω = N |
and kernel ω = N |
. |
||
b |
ω |
b |
ω |
|
(b)Let V Rn be a linear subspace. A projection map is a linear mapping PV : Rn → V which satisfies image (PV ) = V and PV (x) = x for all x V . Show that
PNω = ωωT and PNω = (I − ωωT ) are both projection maps.
(c)Calculate the null space of I −eωθb for ω so(3) and θ (0, 2π) and show that (I − eωθb ) : Nω → Nω is bijective.
|
A = (I |
eωθ )ω + ωωT θ, where θ |
|
(0, 2π). Show that |
|||||
(d) Let |
|
3 |
→ |
|
3− |
b |
b |
|
|
A : |
R |
|
R |
is |
|
|
|
||
|
|
|
|
invertible. |
|
|
|||
10.Planar rotational motion
Let SO(2) be the set of all 2 × 2 orthogonal matrices with determinant equal to +1.
(a)Show that SO(2) can be identified with the S1, the unit circle in R2.
(b)Let ω R be a real number and define ωb so(2) as the skew-symmetric matrix
|
ω = |
0 |
−ω . |
|
Show that |
b |
ω |
0 |
|
eωθ = cos ωθ |
− sin ωθ . |
|||
b |
sin ωθ |
cos ωθ |
|
|
Is the exponential map exp : so(2) → SO(2) surjective? injective?
75
(c)Show that for R SO(2) and ωb so(2), RωRb T = ωb.
11.Planar rigid body transformations
A transformation g = (p, R) SE(2) consists of a translation p R2 and a 2×2 rotation matrix R. We represent this in homogeneous
coordinates as a 3 × 3 matrix: |
|
1 . |
|
|
||||
|
|
|
|
g = |
0 |
|
|
|
|
|
|
|
|
R |
p |
|
|
ξ |
se(2) can be represented by a 3 |
|
3 matrix of the form: |
|||||
A twist b |
ω |
v |
|
0 |
|
ω |
× |
2 |
ξ = |
0 |
0 |
ω = ω |
|
−0 |
ω R, v R . |
||
b |
b |
|
b |
|
|
|
|
|
b
The twist coordinates for ξ Note that v is a vector in the
se(2) have the form ξ = (v, ω) R3. plane and ω is a scalar.
(a)Show that the exponential of a twist in se(2) gives a rigid body transformation in SE(2). Consider both the pure translation case, ξ = (v, 0), and the general case, ξ = (v, ω), ω 6= 0.
(b)Show that the planar twists which correspond to pure rotation about a point q and pure translation in a direction v are given by
|
qy |
|
|
|
vx |
|
|
−1 |
|
0 |
|
||||
ξ = |
qx |
|
(pure rotation) |
ξ = vy |
|
(pure translation). |
|
(c)Show that every planar rigid body motion can be described as either pure rotation about a point (called the pole of the motion) or pure translation.
(d) Show that the matrices V s = gg˙ |
−1 and V b = g−1g˙ are both |
|||||
interpret the spatial velocity V s |
|
R3 |
and |
|||
twists. Define and b |
|
R3 |
|
|
|
|
the body velocity V |
b . |
b |
|
|
|
|
|
|
|
|
|||
(e)The adjoint transformation is used to map body velocities V b R3 into spatial velocities V s R3. Show that the adjoint transformation for planar rigid motions is given by
|
|
|
Adg = 0 |
−1x . |
|
|
|
R |
py |
|
|
|
p |
|
12. Verify that for ω R3, kωk 6= 1 |
|
|||
eωθb |
|
ω |
ω2 |
|
= I + kωk sin(kωkθ) + kω2k 1 − cos(kωkθ) . |
||||
|
|
b |
b |
|
76
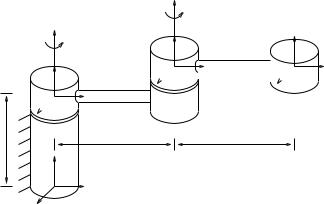
 C2
C2 
 C3
C3
 C1
C1
l0
l1 |
l2 |
C0
Figure 2.17: A two degree of freedom manipulator.
13.Let ξa = (−ωa × qa + hωa, ωa) be the twist associated with a screw having pitch h and axis l = {qa + λωa : λ R}, where all quantities are specified relative to a coordinate frame A.
(a)Let B be a second coordinate frame with configuration gab SE(3). Show that the representation of the twist relative to B is given by
ξb = Ad−1 ξa = Adg |
ba |
ξa. |
gab |
|
(b)Suppose instead that we move the screw via a rigid body transformation g SE(3). Show that the transformed screw can be represented by the twist
ξa′ = Adg ξa,
still relative to the A coordinate frame.
14.Use homogeneous representations to show that the following identities hold:
(a)(Adg )−1 = Adg−1 for all g SE(3).
(b)Adg1g2 = Adg1 Adg2 for all g1, g2 SE(3).
15.Prove Proposition 2.15: Vacb = Adgbc−1 Vabb + Vbcb .
16.Figure 2.17 shows a two degree of freedom manipulator. Let l0, l1, l2 be the link length parameters and θ1, θ2 the joint angle variables of link 1 and link 2, respectively.
(a)Express the position and orientation of frame C3 relative to frame C0 in terms of the joint angle variables and the link parameters.
77
(b)Compute the spatial velocity of C3 relative to C0 as functions of the joint angles and the joint rates.
(c)Compute the body velocity of C3 relative to C0 as functions of the joint angles and the joint rates.
(d)Optional: Find the spatial velocity of the origin of C3 and use this to check your answer for parts (b) and (c).
You may want to use a symbolic math package, such as the one described in Appendix B, to carry out the computations in this exercise.
17.Frame invariance and reciprocal screw systems
An operator is said to be frame invariant if it does not depend on the choice of coordinate frame used to carry out the calculations. Operations which are frame invariant can be computed relative to any coordinate frame, which can simplify calculations.
(a)Show that the reciprocal product between two screws is frame invariant.
(b)Show that the inner product between two twists is not frame invariant.
(c)Calculate a basis for the system of screws reciprocal to a zeropitch screw through a point q. Give a geometric interpretation for the screws which form your basis. (Hint: perform your calculations relative to a specially chosen frame.)
(d)Calculate a basis for the system of screws reciprocal to an infinite pitch screw. Give a geometric interpretation for the screws which form your basis.
(e)Using reciprocal screws, show that three parallel, coplanar, zero-pitch screws are dependent. That is, exhibit a system of four independent screws which are reciprocal to each of the coplanar screws.
18.Hybrid representation of velocity
A seemingly natural way of representing the velocity of a rigid body is to use p˙ to represent the linear velocity and ωs to represent the
angular velocity. We call Vabh = (p,˙ ωs) the hybrid velocity of a rigid body.
(a)Show that the hybrid velocity is related to the body velocity by the relationship
V h = |
R |
0 |
V b |
|
0 |
R |
|
78
and hence represents the velocity of the rigid body relative to a frame attached to the origin of the rigid body, but whose orientation remains fixed relative to the inertial frame.
(b)Consider the motion of three coordinates frames, A, B, and C. Show that the following relationship holds between their hybrid velocities:
Vach = Ad(−Rab pbc ) Vabh + AdRab Vbch.
where Adp denotes the adjoint map corresponding to a pure translation by p and AdR denotes the adjoint map corresponding to pure rotation.
(c)Show that the hybrid velocity of a rigid body is independent of the position of the spatial frame, but not its orientation.
(d)Show that the hybrid velocity of a rigid body is independent of the orientation of the body frame, but not its position.
(e)Interpret a wrench in hybrid coordinates and calculate the change of basis formulas for a change in spatial and/or body frames.
79
80
Chapter 3
Manipulator Kinematics
The kinematics of a robot manipulator describes the relationship between the motion of the joints of the manipulator and the resulting motion of the rigid bodies which form the robot. This chapter gives a description of the kinematics for a general n degree of freedom, open-chain robot manipulator using the tools presented in Chapter 2. We also present a brief treatment of redundant and parallel manipulators using this same framework.
1Introduction
Most modern manipulators consist of a set of rigid links connected together by a set of joints. Motors are attached to the joints so that the overall motion of the mechanism can be controlled to perform a given task. A tool, typically a gripper of some sort, is attached to the end of the robot to interact with the environment.
Although any type of joint mechanism can be used to connect the links of a robot, traditionally the joints are chosen from a set of six mechanisms called lower pairs. These special types of joint mechanisms correspond to subgroups of the special Euclidean group SE(3). They represent revolute, prismatic, helical, cylindrical, spherical, and planar joints.
The revolute, prismatic, and helical joints each correspond to screw motions, with the helical joint corresponding to a general screw with fi- nite, nonzero pitch. A cylindrical joint has two independent degrees of freedom and is typically constructed by combining a revolute and a prismatic joint such that their axes are coincident. Revolute and prismatic joints are by far the most common type of joint encountered in robotics.
A spherical joint is a mechanism which is capable of arbitrary rotations. Passive spherical joints often consist of a ball inserted into a socket, and are therefore referred to as ball and socket joints. Unfortunately, this
81
type of mechanism does not work well if the joint is to exert forces and torques, and hence actuated spherical joints are most often constructed by combining three revolute joints (with motors) such that their axes all intersect at a point. The orientation of the joint is then given by
R = eωb1θ1 eωb2θ2 eωb3θ3 ,
where ω1, ω2, ω3 R3 represent the directions of the three axes. This is very similar to an Euler angle parameterization of orientation and has the same limitations in terms of singularities of the mechanism. Spherical mechanisms are often used as wrists in robot manipulators to allow arbitrary orientation of the gripper or tool at the end of the robot.
Planar joints allow for arbitrary translation and rotation in the plane. Along with helical joints, they are the least commonly used of the lowerpair mechanisms. A planar joint can be built from a revolute joint attached to two independent prismatic joints. The motion of a planar joint is restricted to SE(2), regarded as a 3-dimensional subgroup of SE(3).
Modern robot manipulators, and kinematic mechanisms in general, are typically constructed by connecting di erent lower-pair joints together using rigid links. Since each of the joints restricts the motion of adjacent links to a subgroup of SE(3), the tools developed in the last chapter provide a natural starting point for the analysis of such mechanisms. In this chapter and the next, we concentrate on the kinematics, dynamics, and control of open-chain robot manipulators, in which a number of links are attached serially by a set of actuated joints. By controlling the forces and torques on each of the links, we seek to move the robot in a specified way.
The heart of the formulation which we present here is the product of exponentials formula, which represents the kinematics of an open-chain mechanism as the product of exponentials of twists. This setting works whenever the joints of the robot consist of either revolute, prismatic, or helical joints, which is the case for practically all commercially available robot manipulators. It provides a global, geometric representation of the kinematics of a manipulator which greatly simplifies the analysis of the mechanism and provides a very structured parameterization for openchain robots.
This chapter is organized as follows: Section 2 contains a derivation of the product of exponentials formula for the forward kinematics of an arbitrary open-chain manipulator. We concentrate on the most general case, where the end-e ector configuration lies in SE(3). Section 3 discusses the inverse problem of finding a set of joint angles which causes the end-e ector to have a desired configuration. We make extensive use of a set of subproblems originally proposed by Paden and Kahan which are very closely related to the exponential representation of rigid body motion. Section 4 derives the velocity and force relationships between
82
