Глава восьмая. Однородные цифровые интегрирующие структуры

8.1. Цифровые интеграторы для оцис

На основе разработанных цифровых решающих блоков (цифровых интеграторов) рассмотрим принципы построения одного класса высокопроизводительных многопроцессорных вычислительных систем – однородных вычислительных систем [69, 70, 101]. Такие МВС названы однородными цифровыми интегрирующими структурами (ОЦИС). [21, 22, 23, 77].

Однородные цифровые интегрирующие структуры представляют собой класс специализированных вычислительных систем, предназначенных для решения широкого круга непрерывных математических задач, описываемых системами дифференциальных уравнений, в частности для моделирования сложных динамических объектов и для управления подобными объектами.

Рис. 8.1

Однородные цифровые интегрирующие структуры (рис. 8.1) включают значительное число параллельно работающих специализированных процессоров Пк, систему коммутации входов и выходов процессоров КС и систему управления СУ. Процессоры ОЦИС выполняют, как правило, три типа операций: суммирование, интегрирование и экстраполяцию, к которым часто добавляются некоторые логические операции, а также операция квантования переменных. Основной операцией каждого процессора ОЦИС является операция интегрирования, в связи с чем процессоры ОЦИС часто называются цифровыми интеграторами.

Цифровые интеграторы могут быть построены для реализации операции интегрирования по Риману

(8.1)

или для реализации операции интегрирования по Стилтьесу

(8.2)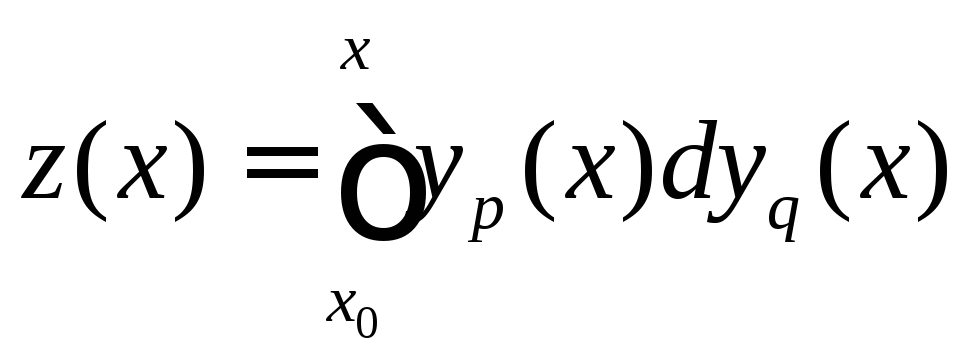

.

Те интеграторы, которые предназначены для выполнения операции интегрирования по Стилтьесу, могут, очевидно, выполнить и интегрирование по Риману, в том случае, когда .

Операция интегрирования по Стилтьесу является более универсальной и позволяет образовывать любые негипертрансцендентные функциональные зависимости, тогда как операция интегрирования по Риману такой возможности не дает. Поэтому процессоры ОЦИС (цифровые интеграторы) следует конструировать для выполнения операции интегрирования по Стилтьесу. В дальнейшем основное внимание уделяется интеграторам, выполняющим операцию интегрирования по Стилтьесу.

В основу алгоритмов работы и синтеза структуры цифровых интеграторов положены формулы численного интегрирования по Стилтьесу [36, 76]. Различают интерполяционные и экстраполяционные формулы численного интегрирования по Стилтьесу. Интерполяционные формулы являются более простыми, но приводят к необходимости прибегать к итерационному процессу вычислений. Экстраполяционные формулы сложнее интерполяционных, так как требуют экстраполяции приращений переменных, но позволяют вычислить приращения интегралов за одну итерацию, обеспечивая тем самым высокое быстродействие.

Существуют интерполяционные формулы численного интегрирования по Стилтьесу различной точности, в том числе:

формула прямоугольников

(8.3)

формула трапеций

;

(8.4)

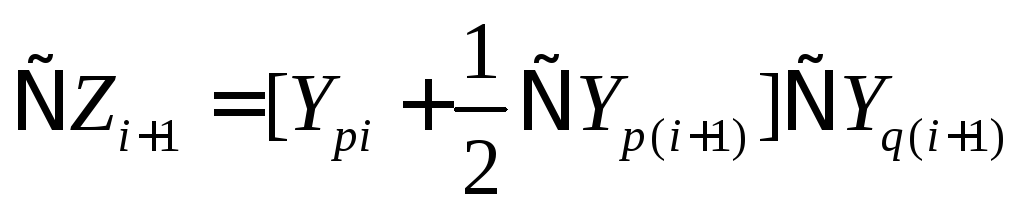
формула квадратичных парабол

(8.5)

;

формула кубичных парабол

(8.6)

.

Здесь – приращение искомого интеграла Z(x) на интервале от i-й до (i+1)-й точки интегрирования;

и соответственно приращения подынтегральной функции Ур(Х) и переменной интегрирования Уq(Х).

Могут быть получены интерполяционные формулы численного интегрирования по Стилтьесу и более высокого порядка точности. Погрешность интерполяционных формул на одном шаге интегрирования зависит от шага интегрирования и производных функций Ур(Х) и Уq(Х) , а также от порядка точности формулы интегрирования n:

(8.7)

.

Подробный анализ показывает, что при повышении порядка точности формулы интегрирования отношение производительности (скорости работы) цифрового интегратора к затратам оборудования вначале быстро растет, а затем начинает убывать. Оптимальной с точки зрения производительности на единицу оборудования является формула квадратичных парабол (8.5). На практике, как правило, используется либо формула квадратичных парабол, либо более простая формула трапеций, которые обеспечивают высокое быстродействие цифровых интеграторов и в то же время ограничивают затраты оборудования разумными пределами.

Широко распространены также цифровые интеграторы, построенные на основе простейшей формулы прямоугольников. Такие интеграторы привлекательны тем, что очень просты по своей структуре. Основным их недостатком является низкая скорость вычислений, вследствие чего цифровые интеграторы, основанные на формуле прямоугольников, можно использовать лишь для моделирования медленно действующих динамических систем и для управления подобными системами.

Заметим, что если переменная интегрирования изменяется по линейному закону , то интерполяционные формулы численного интегрирования по Стилтьесу (8.38.6) превращаются в обычные интерполяционные формулы численного интегрирования Адамса:

(8.8)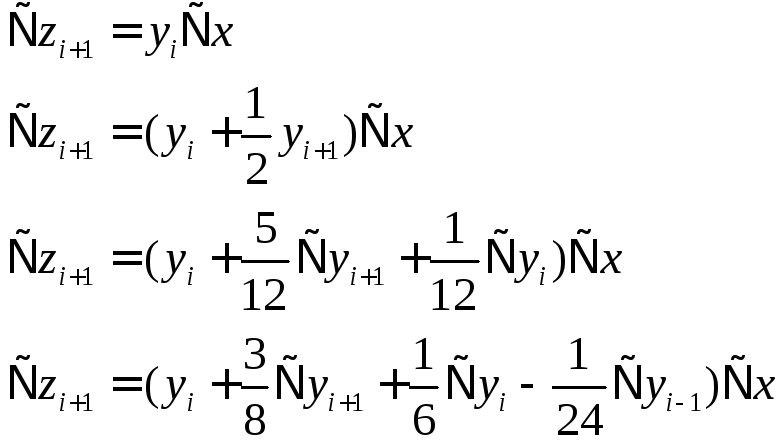

;

;

;

.

Чтобы избежать итерационного процесса вычислений, который необходим при интерполяционных формулах численного интегрирования и который существенно снижает скорость вычислений, следует использовать для синтеза цифровых интеграторов экстраполяционные формулы численного интегрирования по Стилтьесу. В частности могут быть использованы следующие экстраполяционные формулы численного интегрирования:

формула прямоугольников

(8.9)

;

формула трапеций

(8.10)

;

формула квадратичных парабол

(8.11)

;

формула кубичных парабол

(8.12)

,

а также формулы более высокого порядка точности. Погрешности метода Мi приведенных экстраполяционных формул совпадают с погрешностями рассмотренных выше интерполяционных формул того же порядка точности.

Как видно, экстраполяционные формулы численного интегрирования по Стилтьесу отличаются от интерполяционных лишь тем, что в правые их части входят не точные приращения подынтегральной функции и функции интегрирования _, а проэкстраполированные значения и , вычисляемые с помощью формул экстраполяции через предыдущие значения приращений. Следовательно, цифровые интеграторы экстраполяционного типа должны содержать экстраполяторы приращений.

Цифровые интеграторы как интерполяционного, так и экстраполяционного типа работают с переменными, представленными в цифровой форме и содержащими конечное число разрядов. Для простоты обмена информацией между интеграторами необходимо, чтобы все переменные, в том числе переменная интегрирования Yq(х) подынтегральная функция Ур(х) и интеграл z(x) содержали одинаковое число разрядов. В то же время нетрудно видеть, что приращение интеграла, вычисленное по формулам численного интегрирования, будет содержать в общем случае удвоенное количество разрядов по сравнению с числом разрядов приращений переменной интегрирования и подынтегральной функции.

В связи с этим возникает необходимость укорачивать длину приращений интеграла, то есть производить квантование приращений интеграла, выделяя квантованную часть приращения интеграла

(8.13)

и остаток интеграла

, (8.14)

вычисляемые с учетом ранее образовавшихся остатков .

При этом для квантованной части приращения интеграла отводится такое же число разрядов, как и для приращений и .

Наиболее простой и точный алгоритм квантования приращений интеграла, учитывающий ранее образованные остатки приращений, записывается в следующей форме:

(8.15)

,

,

где – функция выделения n старших разрядов (слева от запятой), a - функция выделения младших разрядов (справа от запятой).

Квантование приращений приводит к дополнительной погрешности квантования, зависящей от квантов интеграла , подынтегральной функции и переменной интегрирования

(8.16)

.

Различают полноразрядные приращения и, для которых отводится столько же разрядов, сколько содержат переменные и ; многоразрядные приращения, число разрядов которых меньше, чем число разрядов соответствующих переменных, и одноразрядные, для представления которых отведен всего лишь один разряд. Очевидно, что чем больше разрядов отводится для представления переменных, тем меньше кванты переменных и и тем меньше погрешность квантования _.

Общая погрешность цифрового интегратора на одном шаге интегрирования представляет собой сумму погрешностей метода интегрирования и квантования

. (8.17)

Погрешность метода можно изменять лишь за счет выбора порядка n формулы численного интегрирования и за счет изменения шага интегрирования . Погрешность квантования зависит только от квантов переменных и .

Порядок точности формулы численного интегрирования, положенный в основу построения цифрового интегратора, и количество разрядов, отводимое для представления величин и приращений, находятся в достаточно жесткой зависимости друг от друга. Действительно обе составляющие общей погрешности – погрешность метода и погрешность квантования должны иметь одинаковой порядок малости. Если какая-либо из составляющих погрешности будет иметь порядок малости, отличной от другой составляющей, то это приведет к нерациональным затратам оборудования или к снижению точности и скорости интегрирования.

Так, при использовании грубых формул численного интегрирования нет смысла выбирать очень малые кванты переменных, ибо точность работы цифровых интеграторов в результате этого практически не возрастает, но одновременно увеличивается оборудование интегратора, необходимое для хранения информации, и растет время, требующееся для ее переработки. В результате нерационально возрастает объем цифрового интегратора и снижается скорость работы.

Наоборот, в случае использования, например, одноразрядных приращений нет никакого смысла применять для построения цифровых интеграторов точные формулы интегрирования, так как это не приводит к заметному повышению точности интеграторов, но в то же время существенно увеличивает количество необходимого оборудования и снижает скорость работы.

Вследствие этого одноразрядные приращения применяются в цифровых интеграторах одновременно с наиболее грубой формулой интегрирования – формулой прямоугольников. Если цифровые интеграторы строятся на основе более точных формул численного интегрирования, то одновременно должны быть использованы многоразрядные приращения. И наоборот, если в цифровых интеграторах используются многоразрядные приращения, то необходимо одновременно использовать точные формулы численного интегрирования.

Рассмотрим структурные схемы цифровых интеграторов различного типа. Изложенное выше показывает, что цифровой интегратор должен включать схему, реализующую алгоритм численного интегрирования, схему квантования и схему экстраполяции приращений. Кроме этого, так как приращения подынтегральной функции образуются часто в виде суммы выходных приращений других интеграторов, то в структуру цифрового интегратора должен входить сумматор приращений.

Цифровые интеграторы интерполяционного типа не содержат экстраполяторов приращений и состоят из сумматора  интегратора И и квантователя K (рис. 8.2).

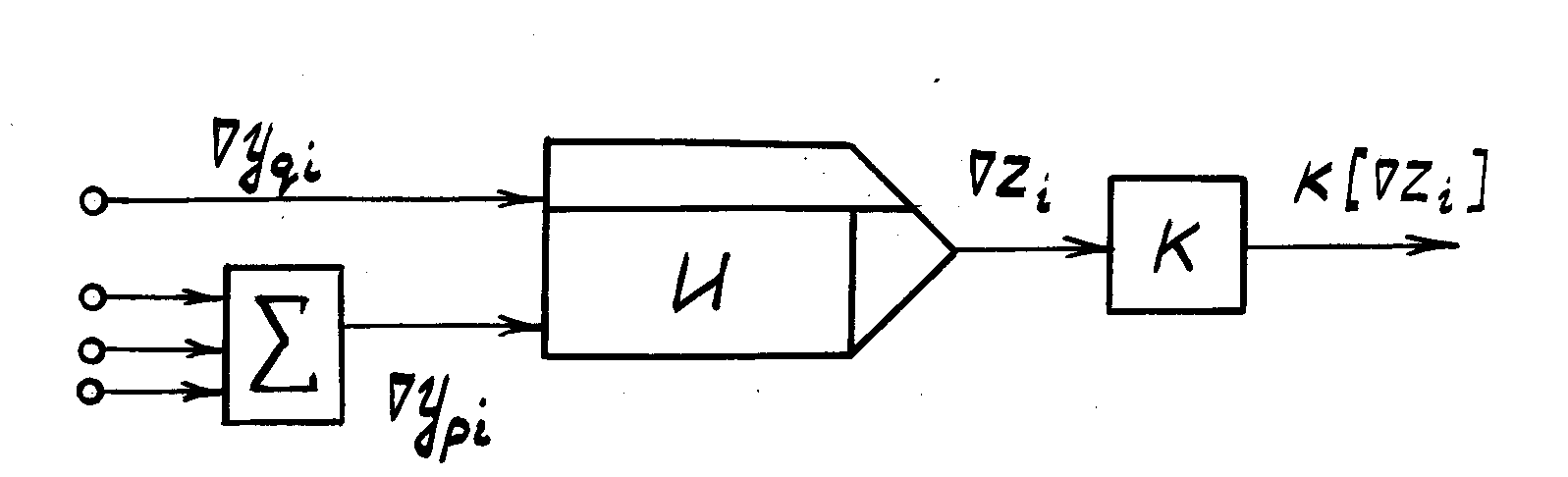
Рис. 8.2

Если для построения интерполяционного интегратора использует­ся формула прямоугольников и одноразрядные приращения, то структурная схема такого интегратора оказывается наиболее простой (рис. 8.3).

Рис. 8.3

Интегрирующая часть этой структурной схемы включает один последовательный сумматор, один регистр и простейшее множительное устройство М , которое умножает величину либо на единицу, либо на нуль, в зависимости от значения одноразрядного приращения . Очень прост и квантователь данного интегратора, который выделяет старший разряд приращения интеграла .

Значительно более высокую точность и скорость позволяет получить цифровой интегратор, работающий с многоразрядными приращениями на основе интерполяционной формулы трапеций (8.4), структурная схема которого приведена на рис. 8.4.

Рис. 8.4

Квантователь такого интегратора реализует алгоритм (8.15). Как видно, структурная, схема интегратора в данном случае усложняется по сравнению с предыдущей незначительно. Вводятся дополнительно лишь один сумматор и одно множительное устройство. В то же время точность и скорость работы такого интегратора повышается на один - два порядка по сравнению с цифровым интегратором, работающим на основе формулы прямоугольников с одноразрядными приращениями.

Рассмотрим структурную схему наиболее оптимального цифрового интегратора (рис. 8.5), в основу которого положена интерполяционная формула квадратичных парабол (8.5). Как видно, структура такого интегратора значительно сложнее структуры интегратора, основанного на формуле трапеций, и тем более сложнее структуры интегратора, работающего с одноразрядными приращениями по формуле прямоугольников. В структуру интегратора, основанного на формуле квадратичных парабол, помимо входного сумматора и выходного квантователя, входят три сумматора , четыре множительных устройства M и три регистра, предназначенных для хранения значений подынтегральной функции и приращений и _.

Рис. 8.5

Такой интегратор работает с многоразрядными приращениями и и обладает весьма высокой скоростью обработки информации и большой точностью. С помощью подобного интегратора можно обеспечить воспроизведение функций, спектр которых содержит гармоники с частотами в десятки, сотни и даже тысячи герц, что дает возможность осуществлять цифровое моделирование в реальном масштабе времени скоростных систем.

Если необходимо реализовать в реальном времени более быстрые процессы, то можно воспользоваться цифровыми интеграторами интерполяционного типа, которые реализуют алгоритм цифрового интегрирования, основанный на форме кубичных парабол (8.6). Структура подобного цифрового интегратора оказывается достаточно сложной (рис. 8.6).

При этом информационная производительность такой схемы на единицу оборудования уменьшается по сравнению с цифровыми интегратором, реализующим формулу квадратичных парабол. Поэтому цифровые интеграторы, в которых используется формула кубичных парабол, следует применять в исключительных случаях, когда требуются весьма высокие точность и скорость работы.

Рис. 8.6

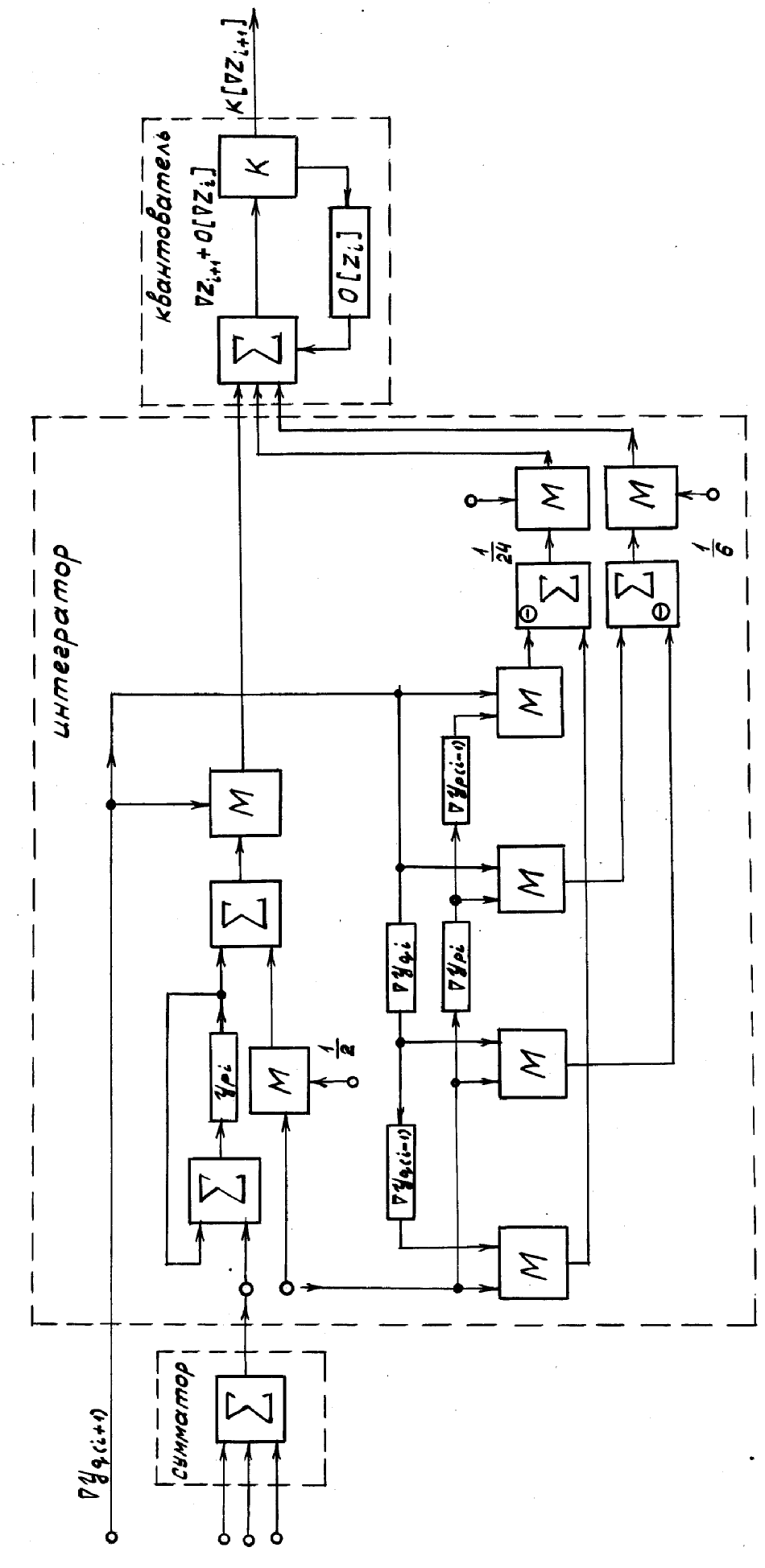
Цифровые интеграторы экстраполяционного типа отличаются от рассмотренных интерполяционных интеграторов лишь тем, что в их структуру дополнительно вводится экстраполятор приращений (рис. 8.7).

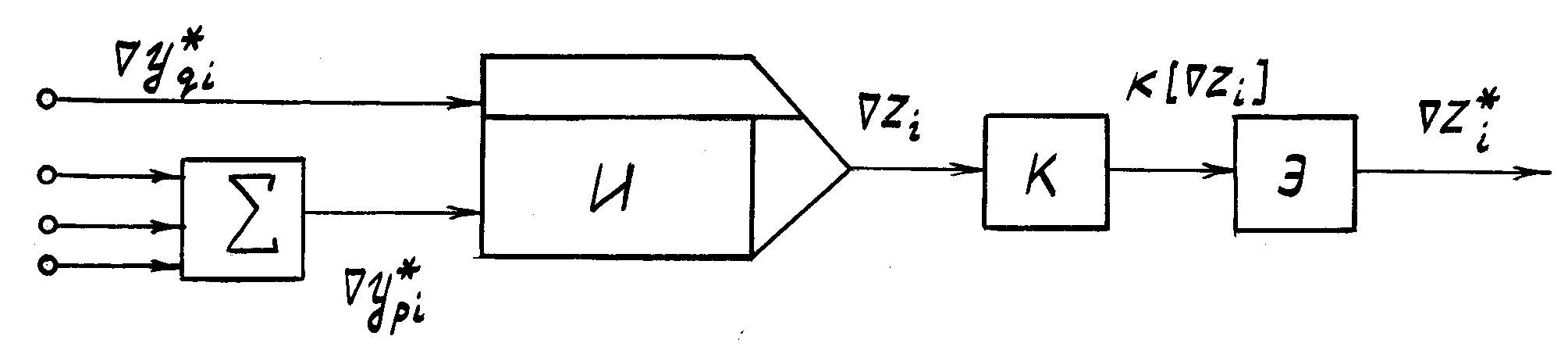
Рис. 8.7

В остальном структура экстраполяционных интеграторов совпадает со структурой интерполяционных интеграторов (рис. 8.3  8.6).

Структура экстраполяторов приращений зависит от порядка точности формулы интегрирования, положенной в основу алгоритма работы интегратора. Для интегратора, работающего по формуле трапеций, экстраполятор реализует формулы экстраполяции (8.10). Структура такого экстраполятора представлена на рис. 8.8.

Рис. 8.8

Для оптимального цифрового интегратора (рис. 8.5), в котором реализуется алгоритм формулы квадратичных парабол, структура экстраполятора приращений (рис. 8.9) оказывается несколько более сложной, однако затраты оборудования на экстраполятор по сравнению с остальными затратами оборудования на интегратор относительно невелики. Поэтому экстраполяционные цифровые интеграторы по своей сложности немного отличаются от интерполяционных интеграторов соответствующего типа.

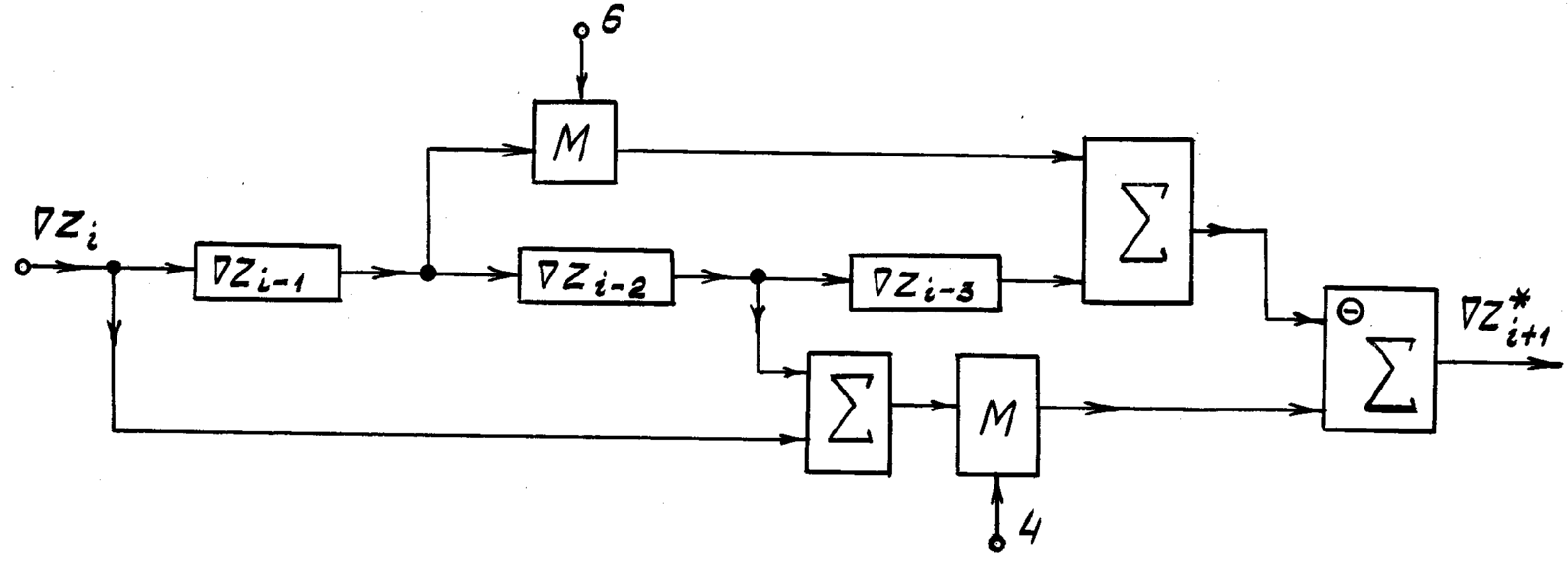
Рис. 8.9

Если необходимо использовать более точный и более быстродействующий экстраполяционный интегратор, реализующий алгоритм формулы кубичных парабол, то экстраполятор строится в соответствии с формулами экстраполяции (8.12).

Цифровые интеграторы могут быть построены как с фиксированной, так и с плавающей запятой. В случае плавающей запятой от одного интегратора к другому должны передаваться не только приращения, но и соответствующие порядки (рис. 8.10).

Рис. 8.10

Принимая во внимание то, что переменные, обрабатываемые в цифровых интегрирующих структурах, изменяются достаточно плавно, можно передавать от интегратора к интегратору не порядки приращений, а их единичные приращения. В этом случае значительно упрощается система передачи информации между интеграторами, а также и структура цифровых интеграторов с плавающей запятой.

Алгоритмы работы цифровых интеграторов с плавающей запятой отличаются от алгоритмов интеграторов с фиксированной запятой следующими особенностями. В цифровых интеграторах с плавающей запятой квантованию подвергаются не приращения интегралов, а мантиссы приращений подынтегральной функции и переменной интегрирования. Кванты в подобных интеграторах являются переменными, вследствие чего алгоритм квантования мантисс приращений несколько усложняется.

Особенность интеграторов с плавающей запятой состоит также в том, что при образовании приращений ивозникает необходимость выравнивать порядки приращений интегралов, приводя их к старшему порядку. Кроме этого, оказывается необходимым приводить к одному порядку подынтегральную функцию и ее приращения с таким расчетом, чтобы не возникло переполнение регистров в сторону старших разрядов.

Перечисленные особенности усложняют цифровые интеграторы с плавающей запятой по сравнению с интеграторами с фиксированной запятой. Однако интеграторы с плавающей запятой согласуются между собой в процессе работы автоматически и не требуют в отличие от интеграторов с фиксированной запятой сложного масштабирования на этапе программирования задач.