4.2. Представление задач для модульных ивс в операторном пространстве

Для отображения задач в модульную интегрирующую вычислительную структуру и разработки системы её универсального математического обеспечения необходимо исходную задачу представлять в специальном операторном пространстве, переход к которому от функционального пространства не требует искусственных приёмов [29, 92].

Задача в операторном пространстве представляется в естественном виде, а реализация теоретико-множественных операций над операторами позволяет ставить и решать проблему построения базиса операторов функций и операций для заданных классов задач. Все это является основой для создания интегрирующих вычислительных структур с универсальным способом организации вычислительного процесса в них.

Будем рассматривать для представления задач в ИВС функциональное пространство - множество всевозможных функций и их суперпозиций на[a, b], которые имеют на [a, b] непрерывные производные до (l–1)-й включительно, Очевидно, что R - линейное метрическое нормированное пространство [92]:

1) в R- определены операции сложения и умножения по правилам векторной алгебры;

2. метрика в R определена как

_(4.2)

2. норма в R определяется как

_(4.3)

.

7. Введем понятие Τ - оператора и пространства Τ - операторов, которые позволяют в удобной форме представлять исходную задачу в ИВС, а также построить математическую модель ИВС. Все дальнейшие рассуждения будем проводить в предположении, что в микропроцессорах (функциональных

модулях) ИВС реализуются системы уравнений Шеннона [76, 109] и, следовательно, нет различий в реализации функций и операций.

Для определения пространства Τ - операторов конкретизируем и формализуем отображение Г:RΛ, которое в дальнейшем будем обозначать как Τ.

О п р е д е л е н и е 1. T-оператором, или моделью схемы Шеннона, будет называться отображение вида , где- некоторая конечная система функций изR; 2^E - множество всех подмножеств системы E  R.

Тогда автоматически получим для Τ-оператора, действующего на функцию f  E из -пространства, следующее определение.

О п р е д е л е н и е 2. Τ-оператором для функции , илиT_f, называ-ется отображение функции f на множество которое является решением системы дифференциальных уравнений Шеннона (СУШ) для функции f .

Тогда E R - область определения Τ-оператора;

2^E - область значений T-оператора.

Причем при конечных Ε область значений Τ-оператора , при счетно-бесконечных Ε область значений Τ-оператора континуальна.

Действие оператора Τ на функцию f, в результате которого получается множество Ε_f , символически представим таким образом:

, где

f - главное значение оператора, - множество побочных значений.

Так как система дифференциальных уравнений Шеннона имеет бесконечное множество решений с точностью до постоянной, то под множеством функций E_f понимается одно из подмножеств множества решений системы дифференциальных уравнений Шеннона, построенное по заданным или выбранным правилам.

П р и м е р. Пусть задана система функций

где

Тогда, если воспользоваться методикой перехода от функций к системам уравнений Шеннона, заключающихся в последовательном дифференцировании функций f_i [76] , можно получить множества в следующем виде:

Таким образом, действие Τ -оператора на функции у₁ и y₂ приводит к следующей записи:

Действие Τ -оператора на элементарную функцию f  R будем записывать в виде где X - область определения f. Если f  R - произвольная функция, т.е. , то, где . Конструкцию назовем комплексом. При

При где *- операция изR – пространства:

если f - элементарная, h - произвольная функции из R.

Факт, определяющий действие Τ-оператора на функцию fR в общем случав, в R - пространстве будем записывать в виде

(4.4)

где - множество решений системы дифферен-циальных уравнений Шеннона для функции f.

Факт, определяющий действие Τ-оператора на произвольную функцию , запишется вR-пространстве в виде:

т.е. множеством решений для комплекса T_foh будет:

если "о" - композиция f, hR и

если и * - операцияR - пространства.

О п р е д е л е н и е 3. Множеств Τ - операторов , задающих отображение некоторого множества функций , и множества операцийв семейство множеств решений систем дифференциальных уравнений Шеннона для функцийи операцийназывается операторным-пространством или пространством T-операторов.

Для определения свойств Τ-операторов сделаем следующие замечания. Пусть X - область определения функции f(X), a Z - область определения оператора . Обозначим черезf_i(z) граничный элемент (конечная точка интервала вычислений) подмножества ·

Тогда функция f(X) совпадает в точке со значением оператора T_f(Z), если В общем случае, функцияf(X) совпадает во всех точках X со значениями оператора T_f (Z) если .

Если существует оператор T_f, то это влечет за собой существование обратного ему оператора такого, что параобразует единичный операторТ_e . Действительно, так как Т_f и есть образы функций в R - пространстве, которые симметричны относительно биссектрисы координатного угла - , т.е. или Оператор Т_е имеет прообразом в R-пространстве функцию. С точки зрения технической интерпретацииТ_е-оператор представляет собой схему вычисления (образование) машинной переменной.

На основании сказанного сформулируем основные свойства Т-операторов.

I. Действие обратного оператора на прообраз прямого в смысле главного значения есть единичный оператор Т_е, который определяется как

т.е.

(4.5)

Это следует из того, что конструкция есть комплекс [29] и, следовательно, ее представление в R будет иметь вид

и в смысле главного значения

где

2. Действие прямого оператора на обратный в смысле главного значения и наоборот есть единичный оператор, т.е.

(4.6)

Это следует из представления в виде.

3. Свойство кратности

(4.7)

Для построения различных моделей с помощью операторов в  - пространстве вводятся следующие операции над Τ-операторами:

1. умножение Τ-оператора на постоянное число

где с  K, K- поле действительных чисел;

, следовательно,

;

(4.8)

2) суммирование операторов

(4.9)

, обобщая.

;

3) произведение операторов

_, обобщая,

(4.10)

.

Операторное пространство  - линейное нормированное метрическое пространство с

1) метрикой, _. (4.11)

где

,

;

^и

2) нормой 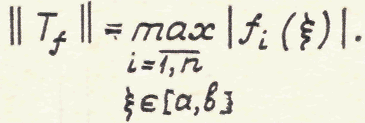(4.12)

Для операторного  - пространства метрика и норма ||T_f || удовлетворяют всем условиям для метрики и нормы, определенных для функционального R-пространства. Покажем это для метрики :

1) при т.е.

, т.к. _;

2) пусть f, g, h  R. тогда

так как

следовательно,

в этих выражениях знак равенства справедлив , когда .

Отсюда

и при имеем

3) метрика симметрична и положительно полуопределена, т.е.

Введем в операторное  - пространство оператор константы Т_с, как , где - нулевой элемент R - пространства.

Исследуем свойства операторного - пространства, касающиеся его линейности:

1) если

T_fi - комплекс;

2) -пространство - абелева группа относительно операции суммирования операторов

так как

и _;

3) в -пространстве существует нулевой элементтакой, что. В самом деле, по определению суммы

_, где ; следовательно ;

4) в -пространстве существует противоположный элемент По определению суммы _, с другой стороны _, следовательно, _.Последнее выражение справедливо, если в R-пространстве вместе с элементом f существует элемент –f, а значит в -пространстве существует элемент . Поэтому противоположным оператором дляT_f будет оператор , обозначенный;

5) операция умножения операторов на числа удовлетворяет условиям:

а) ;

b) , действительно, по определению суммы имеем , следовательно,

;

c) - это происходит в связи с тем, что сумма двух действительных чисел не является операцией суммирования в операторном пространстве;

d)

и

e) _, т.к.;

,

т.к. и .

Следует ответить, что из-за невыполнения свойства для строгости операторное -пространство нужно считать квазилинейным. Это положение не оказывает влияния на дальнейшие теоретические результаты, связанные с построением базиса в операторном пространстве и синтезом математической модели ИВС. Так как обычно в ИВС сумму двух действительных чисел можно заменить одной постоянной величиной, т.е.то свойство операторного пространства свести к операции умножения Τ-оператора на постоянное число: