4.6. Примеры, иллюстрирующие работу базовой машины ивс

П р и м е р 1. Построить модель ИВС (конфигурацию ее архитектурных единиц – функциональных модулей) для преобразования полярных координат в декартовы:

Пусть базис _-пространства включает в себя операторы , т.е. Тогда схема перевода имеет вид:

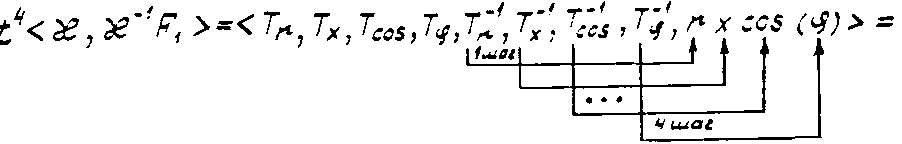
Аналогично для F₂ имеем:

Следовательно,

П р и м е р 2. Требуется построить обобщенную модель ИВС для реализации метода Рунге-Кутта второго порядка при интегрировании дифференциальных уравнений:

в базисе

где Т₊- оператор суммы;

Т_х - оператор произведения;

Т_с - оператор константы 0,5, определяемый в соответствии с [36] как _- нулевой элемент пространства , т.к.

T_h - оператор шага интегрирования;

Т_f - оператор правой части решаемого дифференциального уравнения y' = f(x, y);

Т_у - оператор искомой функции у. Тогда имеем:

здесь оператор является комплексом, т.к. для него необходимо иметь аргументы .

С учетом этого замечания, разрешая уравнение для относительно , получим

где - комплекс (т.е. оператор для ).

Рис. 4.3. Соединение ФМ для преобразования полярных координат в декартовые

Рис. 4.4. Граф коммутации ФМ для реализации метода Рунге-Кутта 2-го порядка

На рис. 4.3 приведен граф коммутации (С - структура) функциональных модулей для вычисления декартовых координат, составленный в соответствии с операторным представлением исходной задачи, а на рис. 4.4 представлен граф коммутации ФМ для реализации метода Рунге-Кутта 2-го порядка.

П р и м е р 3. Представить уравнение задачи навигации в операторной форме:

где

Применяя алгоритм (4.18) к выражениям , получим

где T_g1, - оператор операции сложения (+);

T_g2 - оператор операции умножения ();

T_g3, - оператор операции вычитания (–).

П р и м е р 4. Построить математическую модель ИВС для вычисления координат точек движения манипулятора робота, система уравнений для расчета которых имеет следующий вид [23, 35]:

Пусть базис операторного пространства для исходной задачи имеет вид

.

В результате работы базовой машины W^s, используя выбранный базис, получим операторное представление исходной задачи в следующем виде:

_(4.24)

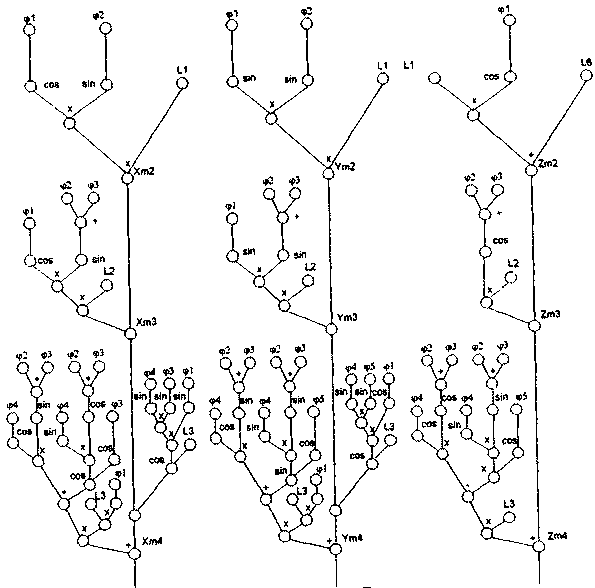
Рис. 4.5. Граф коммутации ФМ

На рис. 4.5 представлен граф коммутации ФМ для вычисления точек движения манипулятора робота, составленный в соответствии с системой (4.24).

Глава пятая. Анализ и синтез универсальных решающих блоков интегрирующих вычислительных структур (ивс)

5.1. Синтез алгоритма универсального решающего блока интегрирующих вычислительных структур

При построении решающих блоков интегрирующих вычислительных структур целесообразно воспользоваться экстраполяционной разностно-квантованной схемой моделирования систем уравнений Шеннона [109], которая в случае численного интегрирования по Стилтьесу с погрешностью порядка имеет следующий вид [36, 76]:

(5.1)

где -функция расчленения, выделяющая из числат старших разрядов [75].

В системе (5.1) использованы относительные квантованные переменные, закодированные в дополнительном коде.

Из общей разностно-квантованной схемы моделирования уравнений Шеннона, используя рассчитанные коэффициенты и беря определенные значения , можно получать конкретные формулы численного интегрирования интеграла Стилтьеса [76].

(5.2)

которые могут быть положены в основу синтеза алгоритмов функционирования решающих блоков ИВС; n = 4, 5, 6, … .

Величины являются постоянными коэффициентами, зависящими от индексов,  и n, и могут быть представлены в следующей форме:

причём значения индексов  изменяются в пределах  + 1    n –  – 3.

В свою очередь коэффициенты вычисляются по выражениям экстраполяционных формул Адамса.

Например, коэффициенты интерполяционных формул численного интегрирования по Стилтьесу имеют следующие значения:

При построении ИВС на основе современных схем микроэлектроники практически используются:

- формула прямоугольников (одноразрядные приращения)

(5.3)

- формула трапеций (многоразрядные приращения)

(5.4)

В параллельных ИВС использование формул квадратичных парабол, кубичных парабол, а также более сложных формул при , реализации решающих блоков пока что затруднительно из-за большого расхода оборудования.

В тех случаях, когда требуется строить решающие блоки, оперирующие с многоразрядными приращениями и обеспечивающие высокую точность вычислений и большое быстродействиепредпочтительнее использовать формулу кубичных парабол, так как она почти эквивалентна по расходу оборудования формуле квадратичных парабол, но обеспечивает более высокую точность вычислений (здесь  - погрешность внешней; - граничная частота, определяющая полосу пропускания частот решающего блока).

В работах [36, 76] заложены основы построения обобщенных цифровых интеграторов, которые, как следует из системы (5.1), должны выполнять операции экстраполяции и суммирования приращений и численного интегрирования. В дальнейших исследованиях [11, 12, 13, 14, 21, 22, 24, 36, 40, 62, 75, 76, 77, 85, 86, 88, 89] и ряде других разработаны универсальные решающие блоки, стандартные операционные и вычислительные блоки, цифровые решающие модули и, наконец, функциональные модули, о которых будет идти речь в следующих разделах.

Для расширения вычислительных и функциональных возможностей УРБ и упрощения процесса набора задач, особенно при управлении и моделировании систем автоматического регулирования, в алгоритм УРБ, кроме вычислительных операций, введены логические операции [14, 76]. При реализации определенных логических функций (гистерезисной, релейной, трения и др.) необходимо вводить те или иные логические операции (ограничения, знака, выделения абсолютного значения функции, выделения максимальных и минимальных значений функции и др.). В работе [14] показано, что при решении задач логического характера на УРБ, оперирующем с одноразрядными приращениями, достаточно в его алгоритм ввести логические операции знака и запрета.

При ограничении, например, функции по уровню, которое часто выполняется в задачах управления движением объектов [27, 36], происходит реализация типичной нелинейной характеристики насыщения. В работах [76, 104] и других показано, что для организации логических функций на УРБ, работающих с многоразрядными приращениями, достаточно ввести логические операции ограничения функции, выделения минимальных и максимальных значений функции, выделения абсолютного значения функции.

Если в алгоритм УРБ (5.1) ввести перечисленные логические операции, то получим алгоритм универсального решающего блока, оперирующего с много-разрядными приращениями и реализующего вычислительные и логические операции:

(5.5)

где Ф, 0 - функции квантования [36, 75, 76]

А - признак операции суммирования приращений;

B - признак операции численного интегрирования с квантованием приращений ;

С - признак операции экстраполяции приращений;

D - признак операции сложения приращений;

Е - признак операции слежения;

Y_o - признак формирования начальных данных.

I - признак операции ограничения, в которой i - номер шага вычислений, т - количество разрядов приращений, n - количество разрядов накапливаемой величины (подынтегральной функции).

Если ограничение происходит сверху, то начальные данные, вносимые в регистр накопления величины у, равны при ограничении снизу; - значение входной функции у в начале вычислений; величины а и b являются соответственно верхним и нижним уровнями ограничения;

L - признак операции выделения min и max функции.

Для этой операции y₁ = +1 при выделении min значений функции и у₁ = -1 при выделении max значений функции;

|L| - признак операции выделения абсолютного значения функции.

Здесь  - коэффициент, зависящий от знаков :

Алгоритм (5.5) является универсальным и он синтезирован с точки зрения обобщения результатов синтеза алгоритмов УРБ. Кроме того, этот алгоритм в общем случае используется для представления машинного алгоритма УРБ и разработки системы автоматического масштабирования переменных и приращений в УРБ ИВС.

Синтезируем машинный алгоритм универсального решающего блока ИВС, используя систему (5.5).

В интегрирующих вычислительных структурах, в которых решающие блоки оперируют над числами с фиксированной запятой, необходимо все математические переменные и их приращения приводить к машинным переменным. Этот процесс осуществляется с помощью операции масштабирования.

Так как в ИВС с фиксированной запятой область представления чисел ограничена по модулю некоторой величиной, то, обозначив множество всех представляемых в структуре чисел через {M_z}, можно отобразить множество {Z} чисел алгоритма (5.5) на множество M_z с помощью операции масштабирования

(5.6)

где M_Z - мантисса числа, P₀ - основание системы счисления, П_Z - порядок числа.

В общем случае приращение интеграла можно вычислить по следующей формуле:

(5.7)

Вычисление этого интеграла в УРБ с фиксированной запятой необходимо производить следующим образом:

(5.8)

Пользуясь выражением (5.6) и приняв в нем P₀ = 2, приращение интеграла (5.7) можно вычислить по следующему машинному соотношению:

. (5.9)

Если в систему (5.5) подставить выражения всех переменных через машинные уравнения (5.6)-(5.9), то получим машинный алгоритм УРБ ИВС, оперирующий с фиксированной запятой [26], в котором из системы (5.5) для упрощения оставлены только операции А, В, С:

(5.10)

Из проведенных рассуждений ясно, что реализация машинных алгоритмов решения задачи – весьма трудоемкий процесс из-за необходимости масштабирования переменных и их приращений. Поэтому разработаны способы автоматического масштабирования. Без автоматического масштабирования принципиально невозможно строить ИВС модульного типа, так как функциональные модули, построенные на основе УРБ, должны в процессе отображения и решения задач перестраиваться.