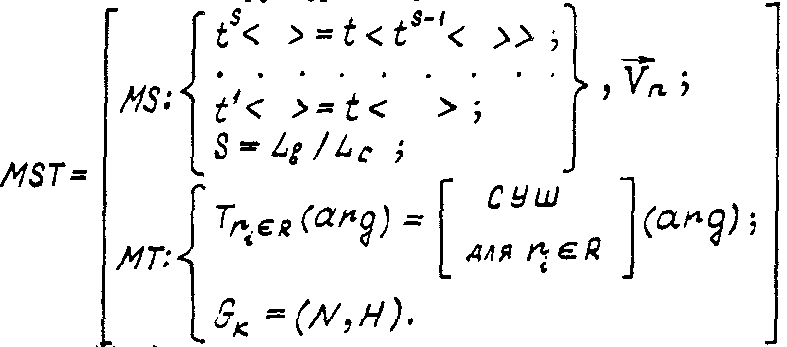- •В.Ф. Гузик проектирование проблемно - ориентированных вычислительных систем
- •Часть 1
- •Предисловие
- •Производительность суперкомпьютеров
- •Глава первая. Концепция построения многопроцессорных вычислительных систем с программируемой архитектурой (мвс па)
- •Глава вторая. Организация математического обеспечения мвс с программируемой архитектурой
- •2.1. Основы математического обеспечения многопроцессорных вычислительных систем с программируемой архитектурой
- •2.2. Организация машинных языков высокого уровня и технология программирования мвс с программируемой архитектурой
- •2.3. Организация параллельных вычислительных процессов в мвс с программируемой архитектурой
- •Глава третья. Проблемно-ориентированные мвс па
- •3.1.Методика перехода от систем дифференциальных и алгебраических уравнений к системе уравнений Шеннона
- •3.1.1.Представление исходной задачи в форме, удобной для реализации на цифровых интегрирующих машинах (цим)
- •3.1.2. Методика перехода от заданных функций к системе уравнений Шеннона
- •3.1.3. Методика перехода от заданных дифференциальных уравнений к системе уравнений Шеннона
- •3.1.4.Методика перехода от систем линейных алгебраических уравнений к системе уравнений Шеннона
- •3.1.5.Получение программных матриц соединений цифровых решающих модулей
- •3.1.6.Методика перехода от программных матриц к схеме соединения цифровых решающих модулей (црм) в цим с жесткими связями
- •3.2.Примеры структурной организации вычислительного процесса в цим.
- •3.2.1.Задача №1
- •3.2.2.Задача №2
- •3.2.3.Задача №3
- •Приложение 3.2
- •3.2.4.Задача №4
- •3.2.5.Задача №5
- •Глава четвёртая. Теоретические основы построения интегрируЮщих вычислительных структур модульного типа
- •4.1. Общая структурно-логическая схема проектирования (анализа и синтеза) модульных ивс
- •4.2. Представление задач для модульных ивс в операторном пространстве
- •4.3. Построение базиса в операторном -пространстве для ивс модульного типа
- •4.4. Разработка эффективного машинного алгоритма выбора базиса в операторном -пространстве
- •4.5. Математическая модель ивс модульного типа на основе t -алгоритмов
- •4.6. Примеры, иллюстрирующие работу базовой машины ивс
- •Глава пятая. Анализ и синтез универсальных решающих блоков интегрирующих вычислительных структур (ивс)
- •5.1. Синтез алгоритма универсального решающего блока интегрирующих вычислительных структур
- •5.2. Разработка алгоритма автоматического масштабирования переменных и приращений в универсальном решающем блока ивс
- •5.3. Построение структурных схем универсальных решающих блоков ивс с автоматическим масштабированием переменных
- •5.4 Разработка алгоритма универсального решающего блока, основанного на принципе цифрового слежения и синтез его структурной схемы
- •5.5.Проектирование решающей части интегрирующих вычислительных структур
- •Глава шестая. Проектирование функциональных модулей интегрирующих вычислительных структур
- •6.1. Исследование принципов построения коммутационных систем модульных интегрирующих вычислительных структур
- •6.2. Разработка волновых каскадных коммутирующих сред для интегрирующих вычислительных структур
- •6.3. Принципы построения цифровых решающих и функциональных модулей ивс
- •6.4.Определение параметров функциональных модулей интегрирующих вычислительных структур
- •6.5.Матричное представление функциональных модулей интегрирующих вычислительных структур
- •6.6. Построение специализированного микропроцессора интегрирующей вычислительной структуры
- •Глава седьмая. Система математического обеспечения модульных интегрирующих вычислительных структур
- •7.1. Структура системы математического обеспечения модульных ивс
- •7.2. Разработка языка структурного программирования высокого уровня для модульных ивс
- •7.3.Разработка транслятора, загрузчика и диспетчера системы программного обеспечения модульных ивс
- •7.4. Построение пакета системных программ для программного обеспечения ивс
- •7.5. Организация вычислительных процессов в модульных ивс
- •Глава восьмая. Однородные цифровые интегрирующие структуры
- •8.1. Цифровые интеграторы для оцис
- •8.2. Интерполяционные и экстраполяционные, одноразрядные и многоразрядные однородные цифровые интегрирующие структуры
- •Глава девятая. Примеры проектирования проблемно- ориентированных мвс на интегрирующих структурах
- •9.1. Моделирующий вычислительный комплекс для исследования систем инерциальной навигации на основе модульных ивс
- •9.2. Применение интегрирующих вычислительных структур для реализации систем управления манипуляционными устройствами автономных роботов
- •9.3. Специализированная вычислительная система для решения задач управления с прогнозированием
- •9.4. Логико-интегрирующие вычислительные структуры
- •Приложение 1 Примерный перечень
- •Министерство образования и науки российской федерации
- •Курс «Технология программирования»
- •Практические задания
- •Курс «Интерфейсы периферийных устройств»
- •Курс «Конструкторско-технологическое обеспечение производства эвм»
- •Библиографический список
- •Оглавление
4.5. Математическая модель ивс модульного типа на основе t -алгоритмов
Для отображения исходных задач из пространства R = Сl[a, b] функций, записанных на некотором формальном входном языке в виде выражений Fi, в модульную ИВС необходимо иметь набор определенных действий или правил отображения, которые позволили бы, основываясь на свойствах операторов из - пространства, перейти от выражений Fi задач из R к операторной их записи в с последующим отображением в интегрирующую вычислительную структуру модульного типа [32, 36] . Для этого определим систему правил, позволяющих сделать такой переход, и построим неформальную математическую модель модульной интегрирующей вычислительной структуры.
Для построения модели ИВС необходимо дать понятие базовой машины, или управляющего автомата ИВС (рис. 4.1).
О п р е д е л е н и е 4. Базовой машиной, или управляющим автоматом, ИВС является в смысле [1] конструкции вида
![]() (4.14)
(4.14)
где W - некоторая система правил сложности S;
G - множество базисных операторов для операций из R;
G-1 - множество обратных базисных операторов для операций из R;
![]() - множество базисных
операторов для функций из R;
- множество базисных
операторов для функций из R;
![]() -
множество обратных базисных операторов
для функций из R.
-
множество обратных базисных операторов
для функций из R.
Под реализацией базовой машины Ws понимается либо комплект программ, либо автомат, предназначенные для организации работы ИВС.
Вследствие
того, что структура операторов для
вычисления функций и реализации операций
одинакова, то под базисом -пространства
понимается просто множество
![]() базисных
Τ
-операторов,
представляющих собой схемы вычисления
по Шеннону функций или реализации
операций из R
-пространства. Тогда базовая машина ИВС
представится как
базисных
Τ
-операторов,
представляющих собой схемы вычисления
по Шеннону функций или реализации
операций из R
-пространства. Тогда базовая машина ИВС
представится как
![]() ,
где
Fi
- выражение,
записанное на входном языке ИВС для
исходной задачи.
,
где
Fi
- выражение,
записанное на входном языке ИВС для
исходной задачи.
Для построения системы правил Ws неформально введем следующие символы:
символ "I" - определяется как связка "или" для построения конструкций при переводе на основе входного языка;
символ < > - определяется как операторные скобки для записи выражений, внешних по отношению к языку (входное выражение для УА);
символы "", "" - определяются как простые выражения при переводе;
4)
символ
![]() -
определяется как шаг перевода входного
слова изFi
в
операторную запись. Если имеется
конструкция
-
определяется как шаг перевода входного
слова изFi
в
операторную запись. Если имеется
конструкция
![]() ,
где
,
где
![]() ,
В
-
входное слово, то она означает символическую
запись комплекса ТА
[B]
на
одном шаге перевода записи Fi
в
операторную форму.
,
В
-
входное слово, то она означает символическую
запись комплекса ТА
[B]
на
одном шаге перевода записи Fi
в
операторную форму.
Рассмотрим процесс построения операторного образа функции f(x) из R в -пространстве. Исходная запись имеет вид:
![]()
На первом шаге алгоритма в записи f(X) находится пара вида ( < оператор операции >, < операция f(Х)>) или ( < оператор функции > , < функция из f(X)>).
Основываясь на свойствах Τ-операторов, имеем:
1) действие обратного оператора на его прообраз (операцию или функцию) в R дает единичный оператор Те (4.5). При конструировании пары выражение f(X) сокращается на обнаруженный прообраз, а в операторной записи остается образ (оператор Tf или Тg) вычеркнутой из f(X) операции или функции.
Например имеем запись
![]()
Пусть
g2
- оператор
операции
![]() ,
,![]() -
оператор функцииsin
x,
тогда действие оператора
-
оператор функцииsin
x,
тогда действие оператора
![]() на
f(X)
даст
пару
на
f(X)
даст
пару
![]() и
в операторной записи останется оператор
g2,
(интегрирования); действие
и
в операторной записи останется оператор
g2,
(интегрирования); действие
![]() на
f(X)
образует
пару
на
f(X)
образует
пару
![]() и
в
операторной записи останется оператор
и
в
операторной записи останется оператор
![]() (функцииsin
x);
(функцииsin
x);
2) действие обратного оператора на прямой дает единичный оператор Тe (4.6) - после обнаружения пар в исходной записи уничтожаются неиспользованные пары по указанному свойству.
В результате реализации всех шагов алгоритма исходная запись превращается в операторное представление следующего вида:
![]() ,
которую, пользуясь свойством кратности
операторов (4.7), можно окончательно
представить как
,
которую, пользуясь свойством кратности
операторов (4.7), можно окончательно
представить как
![]() -
операторная запись исходного выражения
f(X).
-
операторная запись исходного выражения
f(X).
Таким образом, простое выражение определяется как
(4.15)
т.е.
на данном шаге перевода Fi
в
операторную запись образовалcя
комплекс вида
![]() ,
где
,
где![]() -
слово входного языка, кодирующее запись
операции из R-пространства
в исходной задаче. Таким образом, на
данном шаге перевода из Fi
выделилось слово g,
образом которого является оператор
-
слово входного языка, кодирующее запись
операции из R-пространства
в исходной задаче. Таким образом, на
данном шаге перевода из Fi
выделилось слово g,
образом которого является оператор
![]() с
приоритетом k;
с
приоритетом k;
![]() -
остаток входного выражения.
-
остаток входного выражения.
Простое выражение определяется аналогично
(4.16)
таким
образом, на данном шаге перевода Fi
-
в
операторную запись образовался комплекс
![]() ,
где
,
где
![]() -
слово входного языка, кодирующее запись
функции из R-пространства
в исходной задаче. Следовательно, при
переводе из Fi
выделилось
слово f,
образом которого является оператор
-
слово входного языка, кодирующее запись
функции из R-пространства
в исходной задаче. Следовательно, при
переводе из Fi
выделилось
слово f,
образом которого является оператор
![]() с
приоритетом m;
с
приоритетом m;
![]() остаток
входного выражения.
остаток
входного выражения.
О п р е д е л е н и е 5. Конструкция вида
![]()
(4.17)![]()
называется t - операцией над входным выражением Fi.
При
переводе выражения Fi
в операторную запись t
- операция
над Fi
дает
либо шаг перевода с образованием
комплекса
![]() и выделением оператора
и выделением оператора![]() ,
либо шаг перевода с образованием
комплекса
,
либо шаг перевода с образованием
комплекса![]() и
выделением оператора
и
выделением оператора
![]() .
.
Полагая,
что
![]() ,
по
индукции имеем:
,
по
индукции имеем:
![]()

где

Вообще
![]()
Если
длина исходного выражения (количество
слов) Fi
равна
Lb,
а базовая машина WS
работает
со словами длины Lc,
то для получения образа выражения R,
закодированного символом Fi,
в -пространстве
необходимо выполнить
![]() -
операций, каждая из которых переводит
слово
-
операций, каждая из которых переводит
слово![]() в
соответствующий Т
-оператор с приоритетом.
в
соответствующий Т
-оператор с приоритетом.
О п р е д е л е н и е 6. Система правил WS
(4.18)
над
выражением
Fi
,
кодирующим
![]() ,
есть t
- алгоритм.
,
есть t
- алгоритм.
Если
теперь к базовой машине Ws
добавить
дисциплину назначения приоритетов у
T-операторов,
то в совокупности с базисом
![]() получается
модель базовой машины (управляющего
автомата) MS
:
получается
модель базовой машины (управляющего
автомата) MS
:
![]() (4.19)
(4.19)
где
![]() -
процедура назначения приоритетов
-
процедура назначения приоритетов![]()
Построим математическую модель функционального модуля ИВС. Моделью универсального цифрового интегратора (УЦИ) [86], составляющего основу функционального модуля, является система разностных уравнений интегрирования по Стилтьесу для вычисления приращения интеграла по подынтегральной функции и переменной интегрирования.
В интегрирующих вычислительных структурах модульного типа обработка информации ведется на уровне функциональных зависимостей. В этом случае моделью архитектурной единицы ИВС - функционального модуля - является некоторый оператор, представляющий собой реализацию системы дифференциальных уравнений Шеннона для какой-либо функции безотносительно к аргументу. Например, для цифровой интегрирующей машины (ЦИМ), основу которой составляют УЦИ, система уравнений Шеннона для функции y = sin(tg x) включала бы в себя систему для реализации аргумента y = sin(y1), т.е. систему для y1 = tg x· В ИВС то же уравнение реализуется как совокупность операторов Tsin, Ttg, где оператор Tsin[ ] является комплексом, т.е. структура оператора Tsin [ ] не зависит от аргумента.
П р и м е р.
ОператорTsini [ ] представляется СУШ, имеющей вид:

где
![]() и
система дифференциальных уравнений
Шеннона, определяющая внутреннюю
архитектуру ФМ, структурно
и
система дифференциальных уравнений
Шеннона, определяющая внутреннюю
архитектуру ФМ, структурно
реализующего
заданную функциональную зависимость
![]() изR
-
пространства; в ( ) записывается
произвольный аргумент .
Результатом действия оператора Tsin
на
является
значение функции sin
.
изR
-
пространства; в ( ) записывается
произвольный аргумент .
Результатом действия оператора Tsin
на
является
значение функции sin
.
В общем виде математическая модель ФМ ИВС как оператора в операторном -пространстве может быть представлена в следующем виде:
(4.20)
Полной математической моделью ФМ будет система, состоящая из Т -оператора и множества логических функций, обеспечивающих коммутационную полноту ФМ.
В общем
вида коммутацию УЦИ в ФМ
определяет
граф коммутации
![]() ,
гдеN
- количество УЦИ в ФМ; Η
-
отображение,
в общем случае многозначное, которое
каждому элементу
,
гдеN
- количество УЦИ в ФМ; Η
-
отображение,
в общем случае многозначное, которое
каждому элементу
![]() сопоставляет некоторое подмножество
сопоставляет некоторое подмножество![]() ,
такое, что,
,
такое, что,
![]() [18,
19, 22, 33, 36, 77, 81, 82, 97].
[18,
19, 22, 33, 36, 77, 81, 82, 97].
Тогда полную математическую модель ФМ запишем следующим образом
(4.21)
В частности, если для коммутации УЦИ в ΦМ ввести квадратные матрицы Ap, Bq и СУШ представить в векторной форме [76], то из системы (4.21) можно получить полную математическую модель ФМ в следующей записи:

В
(4.22)![]() ,
реализуемую функциональным модулем,
полностью определяют две матрицыAp
и
Bq,
состоящие из нулей и единиц, a
также начальные условия, представленные
вектором
,
реализуемую функциональным модулем,
полностью определяют две матрицыAp
и
Bq,
состоящие из нулей и единиц, a
также начальные условия, представленные
вектором
![]() .
Пользуясь моделью базовой машины
(управляющего автомата) (4.18, 4.19) и моделью
функционального модуля (4.21),
представим математическую модель
интегрирующей вычислительной структуры
модульного типа.
.
Пользуясь моделью базовой машины
(управляющего автомата) (4.18, 4.19) и моделью
функционального модуля (4.21),
представим математическую модель
интегрирующей вычислительной структуры
модульного типа.
(4.23)