
14-es_1 / Высшая математика (РТФ) / умк_Пальчик_Теория вероятностей
.pdfВозьмем и разделим обе части (9.10) на Dx× Dy и вычислим предел при Dx ® 0, Dy ® 0. Тогда
lim |
|
P(x £ X £ x + Dx Ç y £ Y < y + Dy) |
= |
|
|||||||
|
|
|
|||||||||
x →0 |
|
|
DxDy |
|
|
|
|
||||
y→0 |
|
|
|
|
|
|
|
||||
= lim |
|
F (x + Dx, y + Dy) - F (x + Dx, y)) - F (x, y + Dy) - F (x, y)) |
= |
||||||||
|
|
||||||||||
|
x |
→0 |
|
|
DxDy |
||||||
|
y→0 |
|
|
|
|
|
|
|
|||
= |
¶2 F |
|
= f (x, y). |
|
|
(9.11) |
|||||
|
|
|
|
|
|
||||||
|
¶x ¶y |
|
|
|
|
|
|||||
Таким образом, |
f (x, y) = |
¶2 F |
есть предел отношения вероятности |
||||||||
¶x ¶y |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
попадания значений СВ (X, Y) в прямоугольник со сторонами Dx и к пло- щади этого прямоугольника, когда его стороны стремятся к нулю.
Из (9.11) получаем
P(x £ X < x + Dx Ç y £ Y < y + Dy) » f (x, y) dx dy. |
(9.12) |
Выражение f(x, y) dx dy называется элементом вероятности СВ (X, Y). Если же рассматривать не прямоугольник со сторонами Dx, Dy, а область (S), то ее можно разбить прямыми, параллельными осям координат, на элементарные прямоугольники и получаем
P(( X , Y ) Î(S )) = ∫ ∫ f (x, y) dx dy. |
(9.13) |
(S ) |
|
9.5. Свойства f(x, y).
9.5.1. f(x, y) ³ 0.
О. Это следует из свойства 9.3.2, т.е. из того, что F(x, y) является не- убывающей по каждому аргументу, и из свойств пределов. Ä.
9.5.2.
∞ ∞ |
|
∫ ∫ f (x, y) dx dy =1. |
(9.14) |
−∞ −∞
71
О. Это следует из того, что левая часть в (9.14) выражает вероят- ность достоверного события – попадания значений СВ (X, Y) в плоскость R2 (квадрант с бесконечными размерами). Ä.
Выше были отмечены маргинальные распределения компонент X и Y в случае дискретной СВ (X, Y).
Возникает вопрос о маргинальных распределениях компонент X и Y
вслучае непрерывной СВ (X, Y), у которой известна F(x, y) (или f(x, y)).
Всамом деле, если F(x, y) для СВ (X, Y) известна, то воспользуемся равенством (9.9) и свойством 9.3.5. Получаем
lim F (x, y) = |
x |
∞ |
f (x, y) dy = FX (x), |
|
|
∫ |
dx ∫ |
(9.15) |
|||
y→∞ |
|
−∞ |
−∞ |
|
|
|
|
|
|||
и аналогично |
|
|
|
|
|
lim F (x, y) = |
|
∞ |
y |
f (x, y) dy = FY ( y). |
|
|
∫ dx ∫ |
(9.16) |
|||
x→∞ |
−∞ |
−∞ |
|
|
|
|
|
|
|||
(9.16) и (9.15) называют маргинальными функциями распределения компо-
нент X и Y СВ (X, Y).
Теперь из определения плотности распределения 4.11 получаем мар-
гинальные плотности распределения компонент X и Y:
∞ |
|
|
f X (x) = (FX (x))'x = ∫ |
f (x, y) dy, |
(9.17) |
−∞ |
|
|
и |
|
|
∞ |
|
|
fY ( y) = (FY ( y))'y = ∫ |
f (x, y) dx. |
(9.18) |
−∞ |
|
|
9.6. Определение. Случайные величины X и Y называются независи- |
||
мыми, если |
|
|
P( X < x ÇY < y) = P( X < x) × P(Y < y). |
|
|
9.7. Теорема. Если (X, Y) – 2- мерная СВ и компоненты X и Y – |
неза- |
|
висимые СВ, то |
|
|
f(x, y) = fX (x) × fY (y). |
(9.19) |
|
72
О. Ввиду (9.11) f (x, y) = lim |
P(x < X < x + Dx Ç y < Y < y + Dy) |
= |
||
|
|
|||
|
x→0 |
DxDy |
||
|
y→0 |
|
|
|
= (по 9.6) = lim |
P(x < X < x + Dx) × P( y < Y < y + Dy) |
= (4.7), (4.8) = |
||
|
||||
x→0 |
Dx |
Dy |
||
y→0 |
|
|
|
|
=fX (x) fY (y). Ä.
9.8.Пример. СВ (X, Y) имеет плотность распределения
|
|
|
|
|
|
|
2 - x - y; |
0 < x <1Ç 0 < y <1; |
|
|
||||||||
|
|
|
|
f (x, y) = |
0 |
в остальных случаях. |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
Выяснить зависимость компонент X и Y. |
|
|
|
|
|
|
||||||||||||
О. По формулам (9.17) и (9.18) имеем: |
|
|
|
|
|
|
||||||||||||
|
|
|
|
∞ |
1 |
|
|
|
|
10 |
|
10 - |
y |
2 |
10 = |
|||
|
|
|
|
|
|
|
|
|||||||||||
f X (x) = ∫ f (x, y) dy = ∫ |
(2 - x - y) dy = 2 y |
-xy |
|
|
||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
−∞ |
0 |
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
3 |
- x для |
x Î]0,1[. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||
fY ( y) = ∫(2 - x - y) dx = |
- y для y Î]0,1[. |
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f |
|
|
(x) × f ( y) = ( |
3 |
- x) × ( |
3 |
- y) ¹ 2 - x - y = f (x, y). |
|
|
|
||||||||
X |
|
|
|
|
|
|||||||||||||
|
|
Y |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поэтому X и Y – зависимые СВ. |
Ä. |
|
|
|
|
|
|
|
||||||||||
10. Условные законы распределения. Числовые характеристики системы СВ
Пусть (X, Y) – 2- мерная СВ, распределение которой известно (т.е. из- вестна таблица (9.3) или известна f(x, y)).
73

10.1. Определение. Условным распределением компоненты (состав- ляющей) Х СВ (X, Y) называется ее распределение, вычисленное при усло- вии, что компонента Y приняла определенное значение.
Пусть (X, Y) – ДСВ, компоненты которой определены на одном про- странстве элементарных событий, и пусть ее закон распределения задан таблицей (9.3).
Пусть X = xi, а Y принимает любое из значений y1, ..., yj, ..., ym.
Тогда условная вероятность события B = {Y = yj } при условии, что
имеет место |
событие |
A = {X = xi }, вычисляется по |
формуле |
(3.1) |
|||||||
P(B/A) = P(BA)/P(A), то есть |
|
|
|
|
|
|
|
||||
p(y |
|
/ x ) = P((Y = y |
|
) /( X = x )) = |
P(Y = y j Ç X = xi ) |
|
= |
pij |
. |
(10.1) |
|
j |
j |
P( X = xi ) |
|
||||||||
|
i |
|
i |
|
Pi* |
|
|||||
|
|
|
|
|
|
|
|
||||
Если в (10.1) j = 1, m , то совокупность {p(y / xi )} условных вероят- ностей { p( y1 / xi ),K, p( ym / xi )} при X = xi и называют условным распреде-
лением компоненты Y при X = xi .
Это условное распределение удобно записать в виде таблицы:
Y |
Y1 |
... |
yj |
... |
ym |
|
P(y/xi ) |
p(y1 /xi ) |
... |
p(yj /xi ) |
... |
p(ym /xi ) |
(10.2) |
Заметим, что
m |
m |
= (9.5) = Pi* / Pi* |
|
∑ p( y j |
/ xi ) = (10.1) = ( ∑ pij ) / Pi* |
= 1. |
|
j =1 |
j =1 |
|
|
Аналогично условное распределение компоненты X при Y = yj есть совокупность
{p(x /yj )} = {p(x1 / yj ), …, p (xn / yj )}, |
(10.3) |
где |
|
p(xi /yj ) = pi j / P* j. |
(10.4) |
Отметим, что знаменатели формул (10.1) и (10.4) определены в (9.5)
и (9.6).
Пусть теперь (X, Y) − НСВ.
74

Тогда условное распределение компоненты X при условии, что Y
приняла значение y, задается условной функцией распределения компонен- ты X
FX (x/y) = P(X < x/ Y = y). |
(10.5) |
Аналогично |
|
FY (y/x) = P(Y < y/ X = x) |
(10.6) |
есть условная функция распределения компоненты Y при условии X = x. Имеет место следующая
10.2. Теорема. Пусть (X, Y) − непрерывная СВ с непрерывной плот- ностью распределения f(x*, y*). Тогда
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
∫ f (x , y ) dx |
|
|
|
∫ f (x , y ) dx |
|
|
|||
F (x y) = |
|
−∞ |
|
|
|
= |
|
−∞ |
; |
||
|
∞ |
|
|
|
|
fY ( y ) |
|||||
X |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
f (x , y ) dx |
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
y |
|
|
|
|
∫ f (x , y ) dy |
|
|
|
∫ f (x , y ) dy |
|
|
|||
F ( y x) = |
−∞ |
|
|
|
|
= |
−∞ |
|
. |
||
∞ |
|
|
|
|
f X (x ) |
|
|||||
Y |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
f (x , y ) dy |
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
.
(10.7)
(10.8)
Отметим, что обозначения x* и y* введены лишь для того, чтобы вы- делить верхние пределы в интегралах (10.7) и (10.8), которые являются ар- гументами левых частей в (10.7) и (10.8).
Ясно, что в общем случае FX(x/y) есть функция от x, а FY(y/x) есть функция от y. Если они являются дифференцируемыми и f(x, y) − плот- ность распределения СВ (X, Y), то получаем условные плотности распре- деления компоненты X при условии, что Y=y, и компоненты Y при усло- вии, что X=x:
f X (x y) = (FX (x
y) = (FX (x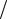 y))′x
y))′x
и
fY ( y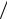 x) = (FY ( y
x) = (FY ( y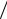 x))′y
x))′y
= (9.18), (10.7) = |
|
f (x, y) |
|
(10.9) |
||
fY ( y) |
||||||
|
|
|
||||
= (9.17),(10.8) = |
f (x, y) |
. |
(10.10) |
|||
|
||||||
|
|
f X (x) |
|
|||
75
Из (10.9) и (10.10) получаем аналог формулы (3.1):
f(x, y) = fY (y) × fX (x/y) = fX (x) × fY (y/x). |
(10.11) |
10.3. Определение. Пусть (X, Y) - 2-мерная СВ с известным зако-
ном распределения (9.3) или f(x, y). Условным математическим ожидани-
ем компоненты X называется МО СВ X, вычисленное при условии, что Y приняла определенное значение Y = y и обозначается M(X/Y). Аналогично определяется и M(Y/X).
Из этого определения и формулы (6.15) получаем формулы для вы- числения M(X/Y) и M(Y/X).
|
n |
× p(xi /Y = y j ) |
|
∑xi |
|||
i=1 |
|
|
|
M ( X /Y ) = |
∞ |
|
|
|
∫ x × f X (x / y) dx |
||
−∞ |
|
|
|
m |
|
× p( y j / X = xi ) |
|
|
∑ y j |
||
j =1 |
|
|
|
M (Y / X ) = |
∞ |
|
|
|
∫ y × fY ( y / x) dy |
||
|
−∞ |
|
|
ДСВ(X, Y)
;(10.12)
НСВ(X, Y)
ДСВ(X, Y)
. (10.13)
НСВ(X, Y)
10.4. Определение. Начальным моментом порядка k+s системы
(X,Y) называется математическое ожидание произведения Xk и Ys, то есть
(ввиду (6.15))
|
|
|
n |
m |
"ДСВ(X,Y) |
|
|
|
∑ ∑ xk ys p |
||
|
|
|
i j ij |
|
|
n |
|
|
i =1 j =1 |
. (10.14) |
|
ks |
= M ( X kY s ) = |
∞ |
∞ |
||
|
|
|
|||
|
|
∫ |
∫ xk ys f (x, y) dxdy |
"НСВ(X,Y) |
|
|
|
−∞ −∞ |
|
||
В частности, n10 = M(XY0) = M(X), n01 = M(X0Y) = M(Y). Совокупность
{M(X), M(Y)} называется математическим ожиданием СВ (X, Y). Геомет-
рически - это координаты средней точки на плоскости XOY, вокруг кото- рой происходит рассеивание значений системы (X, Y).
76

10.5. Определение. Центральным моментом порядка k+s системы (X,Y) называется математическое ожидание произведения (X – M (X))k и
(Y – M (Y))s. |
|
|
|
|
|
|
|
||||
|
|
m |
ks |
= M ( X - M ( X ))k (Y - M (Y ))s = |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
m |
|
|
- M ( X ))k ( y |
|
- M (Y ))s p |
"ДСВ(X,Y) |
|
|
|
|
∑ ∑ (x |
j |
|
|
|||||||
i=1 j =1 |
i |
|
|
ij |
|
. |
(10.15) |
||||
|
|
|
|
|
|
|
|||||
= |
∞ |
∞ |
|
|
|
|
|
|
|
|
|
|
∫ |
∫ (x - M ( X ))k ( y - M (Y ))s f (x, y) dxdy "НСВ(X,Y) |
|
|
|||||||
-∞ -∞ |
|
|
|
|
|
|
|
|
|
||
|
|
m11 называют корреляционным моментом СВ X и Y, или ковариацией |
|||||||||
СВ X и Y и обозначают |
|
|
|
|
|
|
|||||
|
|
|
|
|
μ11 = K XY = COV ( X ,Y ) = M [( X − M ( X ))(Y − M (Y ))] . |
(10.16) |
|||||
|
|
Если (X, Y) - дискретная СВ, то |
|
|
|||||||
|
|
|
|
|
|
|
|
n m |
|
|
|
|
|
|
|
|
K XY |
= ∑ ∑ (xi |
- M ( X ))( y j - M (Y ))pij . |
(10.17) |
|||
i=1 j =1
Если же (X, Y) - непрерывная СВ, то
∞ |
∞ |
|
K XY = ∫ |
∫ (x - M ( X ))( y - M (Y )) f (x, y) dxdy |
(10.18) |
−∞ −∞
10.6. Свойства KXY.
10.6.1. KXY = KYX (очевидно).
10.6.2.Если X и Y независимы, то KXY = ввиду (10.16) и 6.13.3 = =M(X – M (X)) × M(Y – M (Y)) = ввиду (6.26) = 0 × 0 = 0.
10.6.3.KXY = M[XY – M (X)Y – M (Y)X + M(X)M(Y)] = по 6.13 =
=M(XY) – M (X)M(Y) – M (Y)M(X) + M(X)M(Y) = M(XY) – M (X)M(Y). (10.19)
10.6.4. |KXY|£ sX × sY (sX = 
 D( X ), sY =
D( X ), sY = 
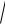 D(Y )). Æ.
D(Y )). Æ.
Если KXY = 0, то не обязательно, что X и Y независимы. В этом случае они называются некоррелированными.
77
10.7. Пример. 2-мерная СВ (X, Y) имеет закон распределения:
X |
–1 |
0 |
1 |
PY |
Y |
|
|
|
|
0 |
1/12 |
1/2 |
1/12 |
2/3 |
2 |
1/12 |
1/6 |
1/12 |
1/3 |
PX |
1/6 |
2/3 |
1/6 |
|
Найти KXY и установить зависимость X и Y.
О. M(X) = (–1) × 1/6 + 0 × 2/3 + 1 × 1/6 = 0, M(Y) = 2/3.
M(XY)=(–1) ×0×1/12+(– 1) ×2×1/12+0×0×1/2+0×2×1/6 + 0×1×1/12 + 2×1×1/12 = 0. По формуле (10.19) KXY = 0 – 0 ×2/3 = 0.
Далее, P(X<0) = 1/6, P(Y<2) = 2/3. Поэтому
P[(X<0)×(Y<2)] = 1/12¹1/6×2/3 = P(X<0)×P(Y<2). Поэтому X и Y зави-
симы, хотя KXY=0.
Ввиду (10.19) формулам (10.17) и (10.18) можно придать более удоб- ный для вычислений вид:
|
n |
m |
|
|
K XY = ∑ ∑ xi y j pij |
- M ( X )M (Y ) ; |
(10.20) |
||
|
i=1 j =1 |
|
|
|
¥ |
¥ |
|
|
|
K XY = ∫ |
∫ |
xyf (x, y) dxdy - M ( X )M (Y ). |
(10.21) |
|
-¥ -¥
Из 6.13.6 следует, что сравнивать X и Y неудобно, если они выража- ются в различных единицах измерения. Поэтому для удобства сравнения
× ×
принято компоненты X и Y нормировать, т.е. перейти к новым СВ X и Y , математические ожидания которых равны нулю, а дисперсии равны 1. Ес- ли положить
|
× |
|
( X - M ( X )) |
|
× |
(Y - M (Y )) |
|
|
|
||
|
|
X = |
, |
Y = |
, |
(10.22) |
|||||
|
|
|
|
||||||||
|
|
|
|
|
sX |
|
sY |
|
|
||
× |
1 |
|
|
|
|
|
|
|
|
|
|
(тогда M ( X ) = |
× M ( X - M ( X )) = 0 по 6.13.6; |
|
|
||||||||
|
|
|
|||||||||
|
sX |
|
|
|
|
|
|
|
|
|
|
|
× |
|
1 |
|
|
|
|
|
D( X ) |
|
|
|
D( X ) = |
|
D( X - M ( X )) = по 6.14.5 = |
=1) , |
|||||||
|
|
|
|
||||||||
|
|
|
s2X |
|
|
|
s2X |
||||
78
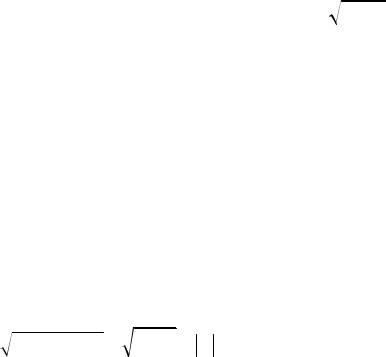
××
то ковариация СВ X и Y называется коэффициентом корреляции и обо- значается
|
|
|
|
|
|
× |
× |
X - M ( X ) |
|
Y - M (Y ) |
|
|
|
|
rXY = |
M ( X ×Y ) = M (( |
) × ( |
)) = |
|
||||||
|
|
sX |
|
|
||||||||
|
|
|
|
|
|
|
|
|
sY |
(10.23) |
||
|
|
1 |
|
|
|
|
разм.X × разм.Y = безразмерная величина). |
|||||
= |
|
|
× K |
|
× ( |
|
||||||
s |
s |
XY |
|
|||||||||
|
|
|
разм.X × разм.Y |
|
|
|
|
|||||
|
|
X |
Y |
|
|
|
|
|
|
|
|
|
rXY уже является безразмерной величиной, так как KXY имеет размер- ность, равную произведению размерностей X и Y по 6.13.6, а sX = 
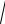 D( X ) - размерность X по 6.14.4.
D( X ) - размерность X по 6.14.4.
10.8. Свойства коэффициента корреляции
10.8.1.|rXY| £ 1.
О. По свойству 6.14.6 дисперсии имеем^ 0£D(X+Y)=D(X)+D(Y)±2COV(XY)=1+1±2rXY=2±2rXY=2(1±rXY). |rXY|£1. Ä.
10.8.2. Если ρXY = ±1, то это равносильно тому, что между СВ X и Y существует линейная функциональная зависимость: Y = b0 + b1X.
О. 1) Пусть Y = b0 + b1X. Тогда
M(Y) = M(b0 + b1X) = b0 + b1M(X);
sY = 
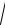 D(b0 + b1X ) =
D(b0 + b1X ) = 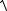
 b12s2X = b1 sX .
b12s2X = b1 sX .
KXY = M[(X – M (X)) × (b0 + b1X – b 0 – b 1M(X))] = M[(X – M (X)) × b1(X – M(X))] =
= M(b1(X – M (X))2) = b1×s2X .
Тогда
rXY = |
K |
XY |
= |
b s2 |
= ±1. |
||
|
1 X |
||||||
|
|
|
|||||
sX sY |
sX |
b1 |
|
||||
|
|
sX |
|||||
Знак ρXY определяется знаком при коэффициенте b1 в функции
Y= b0+b1X.
2)Если r = ± 1, то Y = b0 + b1X. Æ. Ä. 10.8.3. Если rXY ¹ 0, то X и Y зависимы. Æ.
79
Из определения дисперсии 6.9 следует, что центральные моменты m20 и m02 задают дисперсии компонент X и Y соответственно и характери- зуют рассеивание случайной точки в направлении осей Ox и Oy относи- тельно точки (M(X), M(Y)).
Поэтому D(X) можно вычислять по формуле (10.15) при k = 2, s = 0, а D(Y) - по формулам (10.15) при k = 0, s = 2.
Но с учетом (6.27) можно пользоваться более удобными формулами, полагая в (10.15) k = 2, s = 0 и k = 0, s = 2 соответственно
|
m |
|
- M ( X )2 |
"ДСВ(X,Y) |
n |
∑ x2 p |
|||
|
i |
ij |
|
|
D( X ) = ∑ j =1 |
|
|
|
|
i =1 |
|
|
|
(10.24) |
|
|
|
|
|
n |
m |
|
- M (Y )2 |
"ДСВ(X,Y) |
D(Y) = ∑ ∑ y2 p |
||||
|
j |
ij |
|
|
i =1 j =1
и
∞∞
D( X ) = ∫ ∫ x2 f (x, y) dxdy - M ( X )2 "НСВ(X,Y)
−∞ −∞
(10.25)
∞∞
D(Y) = ∫ ∫ y2 f (x, y) dxdy - M (Y )2 "НСВ(X,Y).
−∞ −∞
Теперь может быть доказана следующая
10.9. Теорема.
M ( X ×Y ) = M ( X ) × M (Y ) + M [( X - M ( X ))(Y - M (Y ))]. |
(6.24¢) |
О. Полагаем в формуле (10.14) k = 1, s = 1. Тогда из (10.14) и (10.21) видно, что M(X×Y) – M (X)M(Y) = KXY. Теперь из (10.16) легко следует ут- верждение (6.24'). Ä.
10.10. Замечание. Сравнение теоремы 10.9 и свойства МО 6.13.3 по- казывает, что KXY (и, значит, rXY) является мерой тесноты связи между X и Y. Если KXY ® 0 (или rXY ® 0), то X и Y становятся мало зависимы друг от друга.
80
