14-es_1 / Высшая математика (РТФ) / умк_Пальчик_Теория вероятностей

P(k > 3) =1 - e−3 (1 + 3 + 4,5 + 4,5) » 0,337 .

Ответ: а) 0,229; б) 0,949; в) 0,337.

Задачи для самостоятельного решения

1.С вероятностью 0,8 орудие поражает цель. Произведено 1600 вы- стрелов. Какова вероятность того, что при этом произошло: а) не менее 1200, но не более 1300 попаданий; б) не менее 1200 попаданий?

Ответ: а) 0,9015; б) ≈ 1.

2.40 % деталей изготовлено на заводе № 1, остальные – на заводе

№2. Из всей продукции берут 6 деталей. Какова вероятность того, что сре- ди них окажутся изготовленными заводом № 1: а) две детали; б) хотя бы одна деталь?

Ответ: а) 0,31104; б) 0,936.

3.Монету бросают 100 раз. Сколько раз, вероятнее всего, выпадет при этом герб?

Ответ: 50.

4.В аппаратуре 1000 элементов. Вероятность отказа одного элемента в течение гарантийного срока равна 0,001 и не зависит от работы других элементов. Найти вероятность того, что в течение гарантийного срока от- кажут не менее двух элементов.

Ответ: 0,264.

5.Вероятность изготовления бракованной детали для данного рабо- чего равна 0,3. Найти вероятность того, что из 800 изготовленных им дета- лей число бракованных будет: а) не менее 225, но не более 250; б) 200 де- талей.

Ответ: а) 0,0268; б) 0,062.

6.Вероятность сдачи экзамена для каждого из восьми студентов рав- на 0,8. Найти вероятность того, что экзамен сдадут не менее шести студен- тов. Сколько студентов, вероятнее всего, сдадут экзамен?

Ответ: 0,797; 7.

161

7. ДСВ: законы распределения одномерных ДСВ. Числовые характеристики, функция распределения ДСВ. Примеры ДСВ

Если известно соотношение, устанавливающее связь между всевоз- можными значениями случайной величины (СВ) и вероятностями, с кото- рыми СВ принимает эти значения, то говорят, что задан закон распределе- ния ДСВ (лекция 4), который оформляется в виде таблицы (ряд распреде- ления ДСВ):

Среднее квадратическое отклонение σ(x) = 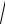D(x) (лекция 6, (6.15), (6.19), (6.20).

Функция распределения ДСВ имеет вид (лекция 4, (4.5'):

F(x)=P(X<x)= ∑ pi .

xi < x

7.1. Пример. Вероятности поражения цели каждым из трех стрелков соответственно равны: 0,7, 0,8, 0,9. СВ X – число поражений цели при ус- ловии, что каждый из стрелков сделал по одному выстрелу. Найти закон распределения, числовые характеристики ДСВ X, функцию распределения.

O. Вероятности поражения цели каждым из стрелков соответственно равны: p1 = 0,7, p2 = 0,8, p3 = 0,9, тогда вероятности того, что цель не поражена,

равны: q1= 1 – p1 = 1 – 0,7 = 0,3; q2 = 1 – p2 = 1 – 0,8 = 0,2; q3 = 1 – p3= 1 – 0,9 = 0,1.

162

СВ X может принимать значения 0, 1, 2, 3 (число поражений цели тремя стрелками). Найдем вероятности, с которыми СВ X принимает соот- ветствующие значения.

P(X = 0) = P(x1) = q1 q 2 q3 = 0,3·0,2·0,1 = 0,006.

P(X = 1) = P(x2) = p1q2q3 + q1p2q3 + q1q2p3 = 0,7·0,2·0,1 + 0,3·0,8·0,1 + + 0,3·0,2·0,9 = 0,092.

P(X = 2) = P(x3) = p1p2q3 + p1q2p3 + q1p2p3 = 0,7·0,8·0,1 + 0,7·0,2·0,9 + + 0,3·0,8·0,9 = 0,398.

P(X = 3) = P(x4) = p1p2p3 = 0,7·0,8·0,9 = 0,504.

Т.о. закон распределения имеет вид:

Проверка: ∑ pi = 0,006 + 0,092 + 0,398 + 0,504 = 1.

Найдем математическое ожидание, дисперсию и среднее квадратиче- ское отклонение:

M(x) =0·0,006 + 1·0,092 + 2·0,398 + 3·0,504 = 2,4. D(x)=02·0,006 + 12·0,092 + 22·0,398 + 32 ·0,504 – (2,4) 2 = 0,46.

σ(x) = D(x) = 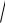0, 46 ≈ 0,68.

Найдем функцию распределения, для этого точками x = 0, 1, 2, 3 ра- зобьем числовую ось на интервалы:

(-∞; 0], (0; 1], (1; 2], (2; 3], (3; +∞). 1). x (-∞; 0], F(x) = P(X<0) = 0.

2). x (0;1], F(x) = P(X<1) = P(X = 0) = P(x1) = 0,006.

3). x (1;2], F(x) = P(X<2) = P(X = 0) + P(X = 1) = P(x1) + P(x2) = = 0,006 + 0,092 = 0,098.

4). x(2;3], F(x) = P(X<3) = P(X = 0) + P(X = 1) + P(X = 2)=

= P(x1) + P(x2) + P(x3) = 0,006 + 0,092 + 0,398 = 0,496.

5). x (3; +∞), F(x) = P(X< ∞ ) = P(X = 0) + P(X = 1) + P(X = 2) + + P(X = 3)= P(x1) + P(x2) + P(x3) + P(x4) = 0,006 + 0,092 + 0,398 + 0,504 = 1.

Т. о. функция распределения ДСВ X имеет вид:

163

Примеры ДСВ

7.2. Пример. Из урны, содержащей 6 белых и 4 черных шара, наугад извлекают три шара. Найти закон распределения СВ X – число черных ша- ров среди трех вынутых.

O. В данном случае имеем гипергеометрическое распределение (лекция 7, (7.5). СВ X может принимать значения, равные 0, 1, 2, 3. Найдем соответствующие им вероятности.

Проверка: ∑ pi = 1/6 + 1/2 + 3/30 + 1/30 = 1.

7.3. Пример. Вероятность наступления некоторого события A в од- ном испытании постоянна и равна p = 0,6. Производится четыре испыта- ния. Найти закон распределения и числовые характеристики СВ X – числа появления события A в четырех испытаниях.

O. В данном случае СВ X имеет биномиальное распределение (лек- ция 7, п. 7.3). СВ X может принимать значения 0, 1, 2, 3, 4, соответствую- щие им вероятности вычисляем по формуле Бернулли:

P(X = k) = Pn(k) = Cnk = pk qn−k .

Для биномиального закона распределения M(x) = np; D(x) = npq. Итак, вычислим вероятности:

P(X = 0) = P4(0) = q4 = 0,44 = 0,0256.

P(X = 1) = P4(1) = C41 × 0,61 × 0,43 = 4 × 0,6 × 0,064 = 0,1536.

P(X = 2) = P4(2) = C42 × 0,62 × 0, 42 =0,3456.

P(X = 3) = P4(3) = C43 × 0,63 × 0,41 = 0,3456.

P(X = 4) = P4(4) = 0,64 = 0,1296.

M(x) = 4·0,6 = 2,4, D(x) = 4·0,6·0,4 = 0,96.

164

7.4. Пример. Охотник, имеющий 6 патронов, стреляет в цель до пер- вого попадания или пока не израсходует все патроны. Найти закон распре- деления СВ X – числа израсходованных патронов, числовые харак- теристики СВ X; вероятность попасть в цель одним выстрелом равна 0,8.

O. Здесь имеет место геометрическое распределение (лекция 7, п. 7.4):

P(X = k) = pqk-1; M(x) = 1/p; D(x) = (1 – p )/p2.

СВ X принимает значения 1, 2, 3, 4, 5, 6.

P(X = 1) = 0,8;

P(X = 2) = 0,2·0,8 = 0,16;

P(X = 3) = 0,22·0,8 = 0,032;

P(X = 4) = 0,23·0,8 = 0,0064;

P(X = 5) = 0,24·0,8 = 0,00128;

P(X = 6) = 0,25·0,8 = 0,00032.

Закон распределения СВ X имеет вид:

Проверка: ∑ pi = 0,8 + 0,16 + 0,032 + 0,0064 + 0,00128 + 0,00032 = 1.

M(x) = 1/0,8 = 1,25; D(x) = 0,2/0,82 = 0,3125.

7.5. Пример. Среднее число машин, прибывающих в автопарк за 1 минуту, равно двум. Найти вероятность того, что за пять минут прибудет шесть машин.

O. Для простейшего (пуассоновского потока) с интенсивностью l

используем формулу (лекция 5, (5.18).

Pt (k ) = (lt)k × e-lt . k !

В данном примере l = 2; t = 5; k = 6.

P5 (6) = (2 ×5)6 e-2×5 = 106 e-10 » 0,06 . 6! 6!

165

Задачи для самостоятельного решения

1.По каналу связи передают пять сообщений. Каждое из них с веро- ятностью 0,3 искажается помехами. Найти закон распределения СВ X – числа сообщений, искаженных помехами; числовые характеристики СВ X.

2.На данном участке дороги вероятность аварии в течение месяца равна 0,02. Каждый месяц регистрируется около 100 проезжающих машин. Найти вероятность того, что за месяц произойдет менее трех аварий.

3.Из партии в 20 изделий, среди которых имеется 6 нестандарт- ных, для проверки качества выбрали случайным образом 7 изделий. Найти закон распределения СВ X – числа нестандартных изделий среди проверяемых.

4.В химчистку в среднем поступает 140 заказов в неделю. Найти ве- роятность того, что в течение двух дней поступит 7 заказов.

5.Однотипные детали испытываются при перегрузочных режимах. Вероятность пройти испытания для каждой из пяти деталей равна 0,7. Ис- пытания заканчиваются после поломки первой же детали. Записать закон распределения СВ X – числа произведенных испытаний. Найти числовые характеристики СВ X.

6.В некотором жилом массиве имеется три продовольственных ма- газина. Вероятность того, что некоторый покупатель за один день посетит магазин № 1, равна 0,4, магазин № 2 – 0,6, магазин № 3 – 0,3.

СВ X – число магазинов, которые посетил покупатель в определенный день. Найти закон распределения, функцию распределения и числовые ха- рактеристики СВ X.

8.НСВ: функция распределения и плотность вероятности НСВ. Числовые характеристики НСВ. Примеры НСВ

При решении задач используем определения функции распределения F(x), плотности вероятности f(x), вероятности попадания СВ X в интервал

[a,b) P(a ≤x <b) (лекция 4, (4.5'), (4.8), (4.12), (4.5), а также определения ма-

тематического ожидания M(x), дисперсии D(x), среднего квадратического отклонения σ(x) (лекция 6, (6.15), (6.19), (6.20).

Итак, функцией распределения СВ X называется функция F(x), опре- деляющая вероятность того, что СВ X примет значение, меньшее, чем x,

т.е.: F(x) = P(X<x).

166

Плотность вероятности: f(x)=F'(x).

b

P(a ≤x <b)= ∫ f (x)dx =F(b) – F (a).

Среднее квадратическое отклонение: s (x)= 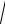D(x) .

8.1. Пример. Дана функция распределения:

Т.о. M(x) = 2,175.

в) P(2≤x<4) = F(4) – F(2) = 1 – (2 3+2)/30 = 2/3, т.к. x = 4 (3;∞) , x =2 (0;3].

8.2. Пример. Плотность вероятности СВ Х задана выражением:

= ax 2 , при 0 £ x £ 3; f (x)

0, при x < 0, x > 3.

Найти: а) коэффициент а; б) функцию распределения F(x); в) вероят- ность того, что в результате опыта СВ Х отклонится от своего математиче- ского ожидания не более, чем на 0,5.

O.

+∞

а) т.к. ∫ f (x)dx =1, то

в). найдем математическое ожидание M(x):

P( x - M (x) < 0,5) = P( x - 2,5 < 0,5) = P(2 < x < 3) =

= F (3) - F (2) =1 - 23 = 19 27 27

Примеры НСВ

Равномерное распределение (лекция 5, (5.21). Говорят, что СВ Х рас- пределена равномерно на интервале [a;b], если ее плотность вероятности и интегральная функция распределения имеют вид:

169

Равномерное распределение является простейшим примером распре- деления непрерывной СВ. Например, ошибка округления до целых единиц при взвешивании однотипных изделий на механических весах имеет рав- номерное распределение.

Показательное распределение (лекция 5, (5.22). СВ Х имеет показа- тельное (экспоненциальное) распределение, если ее плотность вероятности имеет вид:

Показательное распределение часто используется в теории надежно- сти. Например, зачастую время безотказной работы какого-либо элемента имеет показательное распределение. Если Т – время безотказной работы механизма, то F(t) = P(T < t) выражает вероятность выхода из строя меха- низма за время t. Функция R(t) = e-λt называется функцией надежности, где λ – интенсивность отказов, т.е. число отказов в единицу времени.

Заметим, что при показательном распределении возможны любые положительные значения величины t, но большие значения маловероятны:

P(t > λ1 N ) = e− N ,

что уже при N = 7 дает вероятность менее 0,001. Вероятность попадания СВ Х в интервал [a; b]:

P(a ≤ x ≤ b) = F (b) − F (a) = e−λa − e−λb.

8.3. Пример. Автобусы данного маршрута идут с интервалом в 8 ми- нут. Пассажир подходит к остановке в некоторый момент времени. Какова вероятность того, что а) пассажир появится не ранее, чем через 2 минуты после ухода предыдущего автобуса, но не позднее, чем за 3 минуты до от- хода следующего автобуса? б) пассажир, опоздавший на автобус, будет ожидать следующего не более 4-х минут?

170