14-es_1 / Высшая математика (РТФ) / умк_Пальчик_Теория вероятностей

4. Теоремы сложения и умножения вероятностей

При использовании теоремы сложения вероятностей (лекция 2, (2.11) следует вспомнить определение несовместных событий, теоремы умноже- ния (лекция 3, (3.2) – определение независимости событий, определение

условной вероятности.

Так, для двух совместных событий

P(A+B) = P(A)+P(B) – P (AB).

Для трех совместных событий

P(A + B + C) = P(A) + P(B) + P(C) – P (AB) – P (AC) – P (BC) + P(ABC).

Для трех несовместных событий

P(A + B + C) = P(A) + P(B) + P(C).

Для зависимых событий

P(ABC) = P(A)P(B/A)P(C/AB).

Если события A,B,C независимы в совокупности, то

P(ABC) = P(A)P(B)P(C).

4.1. Пример. В ящике 6 изделий 1-го сорта, 8 – 2- го и 10 – 3- го сорта. Найти вероятность того, что наугад взятое изделие – не 3-го сорта.

O. Пусть событие А1 – « взятое изделие – 1- го сорта», А2 – « взятое из- делие – 2- го сорта», А3 – « взятое изделие – 3- го сорта», D – « взятое изделие – не третьего сорта». Событие D означает, что взяли изделие либо 1-го сорта, либо 2-го сорта, т.е. наступило либо событие А1, либо событие А2, т.о.: D = A1 + A2. С другой стороны, наступление события D означает, что собы-

тие А3 не наступило, т.е. наступило противоположное событие A3 . Собы-

тия А1, А2, А3 образуют полную группу событий и являются несовместны- ми (изделие не может одновременно быть и изделием 1-го сорта, и 2-го сорта, и 3-го сорта), поэтому:

P(D) = P(A1 + A2) = P(A1) + P(A2). P(D) = P( A3 ).

151

Найдем вероятности элементарных событий. Число всех возможных исходов (количество всех изделий) n = 6 + 8 + 10 = 24. Число событий, бла- гоприятствующих появлению события А1, m1 = 6, для события A2 m2 = 8, для события A3 m3 = 10. Тогда:

Ответ: 7/12.

4.2. Пример. Вероятность сдать зачет с первого раза для 1-го студен- та равна p1 = 0,6, для 2-го – p2 = 0,7, для 3-го – p3 = 0,75. Найти вероятность того, что из 3-х студентов а) только двое студентов сдадут зачет с первого раза; б) хотя бы один из них сдаст зачет с первого раза.

O.

а) обозначим события:

А1 – «1- й студент сдал зачет с первого раза»; А2 – «2- й студент сдал зачет с первого раза»; А3 – «3- й студент сдал зачет с первого раза».

Тогда P(A1) = p1 = 0,6; P(A2) = p2 = 0,7; P(A3) = p3 = 0,75. D – « только два студента сдадут зачет с первого раза».

D = A1A2 A3 + A1A2 A3 + A1A2 A3 .

Каждое слагаемое является событием, несовместным с каждым из остальных двух (т.е. любые два из них не могут наступить одновременно). Кроме того, события А1, А2, А3 независимы в совокупности, т.к. наступле- ние или не наступление одного из них не влияет на вероятность наступле- ния двух других.

Применяя теорему сложения для несовместных событий и теорему умножения для независимых событий, получим:

P(D) = P( A1)P( A2 )P( A3 ) + P( A1)P( A2 )P( A3 ) + P( A1)P( A2 )P( A3 ) . P( A1) = 1 − P( A1) = 1 – 0,6 = 0,4,

P( A2 ) = 1 − P( A2 ) = 1 – 0,7 = 0,3, P( A3 ) = 1 − P( A3 ) = 1 – 0,75 = 0,25,

P(D) = 0,6 × 0,7 × 0,25 + 0,6 × 0,3 × 0,75 + 0, 4 × 0,7 × 0,75 = 0,45;

152

б) заметим, что вероятность наступления хотя бы одного из собы- тий, независимых в совокупности, равна:

P( A1 + A2 + A3 ) = 1 − P( A1)P( A2 )P( A3 ) .

Т.к. событие В – « хотя бы один из трех студентов сдал зачет с перво- го раза», т.е. B = A1+A2+A3, то

P(B) = 1 – 0,4·0,3·0,25 = 0,97.

Ответ: а) 0,45; б) 0,97.

4.3.Пример. В урне лежат 3 черных шара, 4 белых, и 5 красных. Наудачу одним за другим извлекают 3 шара. Какова вероятность того, что появится сначала белый шар, затем – черный, затем – красный?

O. Пусть событие A – « первым появился белый шар», событие B – «вторым появился черный шар», событие C – « третьим появился красный шар». Искомое событие D = ABC. События A, B, C – зависимы, т.к., на- пример, вероятность наступления событий B, C зависит от наступления или не наступления события A.

Действительно, если событие A не наступило, то значит, первым был извлечен либо черный, либо красный шар, т.е. их количество (или черных, или красных шаров) уменьшилось на единицу, а значит, благоприятст- вующих исходов для события B или события C станет меньше на единицу, следовательно, изменится вероятность их наступления.

Итак, P(A) = 4/12; P(B/A) = 3/11, т.к. после извлечения первого белого шара (событие A наступило) всего осталось 11 шаров, среди них три чер- ных. Аналогично: P(C/AB) = 5/10. Т.о.:

P(D) = P(ABC) = P(A)P(B/A)P(C/AB) = (1/3)·(3/11)·(5/10) = 1/22. Ответ: 1/22.

4.4.Пример. На предприятии брак составляет 1 % от общего выпус- ка изделий. Среди годных изделий – 80 % 1- го сорта. Какова вероятность того, что наугад взятое изделие окажется изделием 1-го сорта, если оно взято из общей массы изготовленной продукции?

O. Искомое событие D – « наугад взятое изделие – 1- го сорта» может наступить только при одновременном наступлении событий:

A – « взятое изделие – годное», B – « изделие – 1- го сорта». Т.е. D = A·B. События A и B зависимы, т.к. изделие не может быть 1-го сорта, если

оно бракованное, т.е. вероятность наступления события B зависит от того, наступило событие A или нет. Поэтому P(D) = P(A)P(B/A).

P(A) = 99/100 = 0,99; P(B/A) = 80/100 = 0,8; P(D) = 0,99·0,8 = 0,792. Ответ: 0,792.

153

Задачи для самостоятельного решения

1.В первом цехе брак составляет 1,7 %, во втором – 2,1 %, в третьем – 0,9 %. Из всех деталей, изготовленных тремя цехами, наудачу берут три детали. Найти вероятность того, что а) хотя бы одна из них оказалась бра- кованной; б) две детали оказались бракованными.

Ответ: а) 0,124; б) 0,004.

2.В ящике лежат 8 красных, 10 зеленых и 12 синих шаров, одинако- вых на ощупь. Наудачу вынимают три шара. Какова вероятность того, что хотя бы два из них одного цвета?

Ответ: 0,236.

3.Экзаменационный билет содержит четыре вопроса. Вероятность того, что студент ответит на 1-ый вопрос, равна 0,9, на второй – 0,8, на третий – 0,85, на четвертый – 0,7. Найти вероятность того, что студент от- ветит а) хотя бы на один вопрос; б) только на два вопроса.

Ответ: а) 0,9991; б) 0,1379.

4.Вероятности пятилетней службы каждой из трех деталей соответ- ственно равны: 0,4, 0,6, 0,8. Найти вероятность того, что пять лет прослу- жат: а) не менее двух деталей; б) хотя бы одна деталь; в) только одна де- таль.

Ответ: а) 0,656, б) 0,952; в) 0,296.

5.По одной и той же мишени производят по одному выстрелу с дис- танций в 1000, 800 и 500 метров. Вероятности попадания с каждой дистан- ции соответственно равны: 0,8, 0,7, 0,6. Найти вероятность того, что про- изойдет: а) два попадания; б) не менее двух попаданий.

Ответ: а) 0,452; б) 0,788.

6.В мастерскую по ремонту бытовой техники поступили две партии деталей определенного типа. В первой партии деталей в три раза больше, чем во второй. Из общего числа деталей мастер берет две первые попав- шиеся детали. Чему равна вероятность того, что обе детали окажутся а) из какой-либо одной партии; б) из различных партий?

Ответ: а) 5/8; б) 3/8.

7.Вероятность повреждения изделия при погрузке на автомашину равна 0,05, при перевозке – 0,02, при разгрузке – 0,01. Найти вероятность доставки изделия: а) с повреждением хотя бы по одной из указанных при- чин; б) с повреждением вследствие двух причин.

Ответ: а) 0,078; б) 0,00167.

154

5. Формула полной вероятности, формула Байеса

Если событие A может произойти одновременно только с одним из несовместных событий H1, H2,…, H n, образующих полную группу событий (гипотез), то вероятность P(A) определяется по формуле полной вероятно-

сти (лекция 3, (3.6):

n

P( A) = ∑ P(Hk )P( A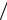 Hk ) .

k =1

Если же событие A уже наступило, то пересчет вероятностей гипотез производится по формуле Байеса (лекция 3, (3.7):

P(Hk / A) = P(Hk ) × P( A / Hk ) ,

P( A)

где P(A) вычисляется по формуле полной вероятности.

5.1. Пример. Некоторая продукция изготавливается на 3-х заводах. 1-ый завод изготавливает 30 % продукции, 2-ой – 45 %, 3- ий – 25 %. Из- вестно, что на 1-м заводе брак составляет 2 %, на 2-ом – 1,5 %, на 3-м – 1 %.

Найти вероятность того, что:

а) взятая наудачу из общей массы единица продукции окажется год- ной (не бракованной);

б) единица продукции, оказавшаяся годной, изготовлена на заводе №1.

O.

а) пусть событие A – « взятая наудачу продукция – годная»; H1 – « наудачу взятая продукция изготовлена на заводе №1»; H2 – « наудачу взятая продукция изготовлена на заводе №2»; H3 – « наудачу взятая продукция изготовлена на заводе №3».

Здесь события H1, H2, H3 образуют полную группу событий (описы- вают все возможные исходы испытания).

Вычислим вероятности гипотез и условные вероятности:

P(H1) = 30/100 = 0,3; P(H2) = 45/100 = 0,45; P(H3) = 25/100 = 0,25;

P(A/H1) = 98/100 = 0,98; P(A/H2) = 98,5/100 = 0,985; P(A/H3) = 99/100 = 0,99.

По формуле полной вероятности

P(A) = 0,3·0,98 + 0,45·0,985 + 0,25·0,99 = 0,98475;

155

б) т.к. событие A уже наступило, то пересчет вероятности гипотезы

H1 произведем по формуле Байеса:

P(H1 / A) = P(H1) × P( A / H1) = 0,3 × 0,98 ≈ 0, 299 .

P( A) 0,98475

Ответ: а) 0,98475; б) 0,299.

5.2. Пример. В белом ящике лежат 12 красных и 6 одинаковых на ощупь синих шаров. В черном ящике лежат 15 красных и 10 синих шаров. Бросается игральная кость. Если число выпавших очков кратно трем, то наудачу вынимают шар из белого ящика, если нет – из черного ящика. Ка- кова вероятность того, что: а) вынутый шар – красный?; б) вынули крас- ный шар из белого ящика?

O.

а) обозначим события:

A – « вынули красный шар»;

H1 – « шар достали из белого ящика, т.е. выпало число очков, кратное трем»;

H2 – «шар достали из черного ящика, т.е. выпало число очков, не кратное трем».

Найдем вероятности гипотез при испытании (опыте) «бросается иг- ральная кость». Число всех возможных исходов данного опыта равно n = 6. (D1 – « выпало одно очко», D2 – « выпало два очка», … D6 – « выпало шесть очков»). Число исходов, благоприятствующих появлению события (гипо- тезы) H1 m1 = 2 (наступило событие D3 или событие D6). Число исходов, благоприятствующих появлению гипотезы H2, равно m2 = 4 (наступило со- бытие D1, или D2, или D4, или D5).

Т.о. P(H1) = m1/n = 2/6 = 1/3; P(H2) = m2/n = 4/6 = 2/3.

Определим условные вероятности, т.е. вероятности наступления со- бытия А, при условии, что наступило событие H1 и при условии, что на- ступило событие H2.

Вероятность взять красный шар, при условии, что он был взят из бе- лого ящика, равна:

По формуле полной вероятности

P(A) = 1 × 2 + 2 × 3 = 28 ; 3 3 3 5 45

б) событие A уже произошло, т.е. в результате эксперимента был вы- нут красный шар. Пересчитаем вероятность того, что он был вынут из бе- лого ящика, по формуле Байеса:

Ответ: а) 28/45; б) 5/14.

Задания для самостоятельного решения

1.Имеется три урны. В первой находятся 3 белых и 5 черных шаров, во второй – 4 белых и 3 черных, в 3-й – 5 белых и 6 черных шаров. Найти вероятность того, что: а) шар из наугад выбранной урны окажется белого цвета; б) если выбранный шар оказался белого цвета, то какова вероят- ность того, что он был взят из 2-ой урны?

Ответ: а) 0,467; б) 0,408.

2.В спортивной команде два человека имеют 1-й разряд, три – вто- рой, пять – 3- й. На соревнования случайным образом отбирают одного спортсмена. Вероятность выиграть соревнование для спортсмена 1-го раз- ряда равна 0,9, 2-го – 0,8; 3- го – 0,6. Какова вероятность того, что:

а) выбранный спортсмен выиграет соревнования?

б) спортсмен, выигравший соревнование, имеет 2-ой разряд?

Ответ: а) 0,72; б) 0,33.

3.Имеется три партии одинаковых изделий по 10, 20 и 30 штук, при- чем в 1-й партии два, во второй – три, в 3-й – четыре нестандартных изде- лия. Найти вероятность того, что изделие, наугад взятое из общей массы продукции, окажется нестандартным.

Ответ: 3/20.

4.В магазине имеется три кассовых аппарата. Покупатель может с одинаковой вероятностью подойти к одному из них. Первый кассир может

157

обслужить покупателя в течение 1 минуты с вероятностью 0,9, второй кас- сир – с вероятностью 0,8, третий – с вероятностью 0,7. Найти вероятность того, что покупатель, придя в магазин, будет обслужен в течение 1 минуты.

Ответ: 0,8.

5. В первой коробке из 10 деталей 3 бракованных, во второй из 15 – 5 бракованных. Из второй коробки в первую переложили одну деталь, а за- тем из нее наугад взяли две детали. Найти вероятность того, что они оказа- лись бракованными.

Ответ: 0,097.

6. Последовательности испытаний. Формула Бернулли, предельные теоремы при повторных испытаниях

Вероятность того, что в n независимых испытаниях, в каждом из ко- торых событие A появляется с вероятностью p, оно наступит k раз, вычис- ляется по формуле Бернулли (лекция 5, (5.1):

Pn (k ) = Cnk × pk × qn−k ,(где q =1 - p) .

Эту формулу удобно применять при небольших значениях n. При больших значениях n (n ® ¥) применяются формулы приближенного вы- числения: формула Пуассона (5.7') (при малом значении p), локальная и интегральная теоремы Муавра – Лапласа (5.19), (5.20):

j(x) определяется по таблице.

Pn (k1,k2 ) » Ф( x¢¢) - Ф( x¢)

x¢ = k1 - np ; x¢¢ = k2 - np .

Ф(x) определяется по таблице. Наивероятнейшее число появления события при n испытаниях вычисляется по формуле (5.6)

np – q ≤ k0 ≤ np + p.

6.1. Пример. По цели производится 5 независимых выстрелов. Веро- ятность попадания в цель при одном выстреле равна 0,7. Найти:

а) вероятность 3-х попаданий; б) вероятность попадания не менее 3-х раз;

в) наивероятнейшее число попаданий.

O.

а) Здесь n = 5, p = 0,7. Применяем формулу Бернулли:

ного интервала выбираем единственное целое число k = 4. Т.е., вероятнее всего, при пяти выстрелах будет 4 попадания.

Ответ: а) 0,09261; б) 0,62083; в) 4.

6.2. Пример. Вероятность производства бракованной детали равна 0,008. Найти вероятность того, что из взятых 1000 деталей 10 окажутся бракованными.

O. При достаточно больших значениях n = 1000 и малой вероятности p = 0,008 (когда выполняется приближенное равенство np ≈ npq) применя- ется формула Пуассона:

l = np =1000 × 0,008 = 8 ; npq =1000 × 0,008 × 0,992 = 7,936 ≈ 8.

P (10) » 810 × e−8 » 0,378 .

1000

10!

Ответ: 0,378.

159

6.3. Пример. Вероятность того, что станок потребует переналадки в течение одного дня, равна 0,2. Найти вероятность того, что в течение 30 дней станок будет переналажен а) 5 раз; б) более 10 раз.

O. Здесь n достаточно велико. Применим локальную и интегральную

F(10,95) = 0,5.

Заметим, что для всех x > 5, F(x) » 0,5. Т.о.

P30 (10 ≤ k ≤ 30) ≈ Φ(10,95) − Φ(1,83) = 0,5 − 0,4664 = 0,0336 .

Ответ: а) 0,161; б) 0,0336.

6.4. Пример. Завод отправил в магазин 1000 изделий. Вероятность повреждения изделия в пути p = 0,003. Найти вероятность того, что в пути будет повреждено: а) два изделия; б) хотя бы одно изделие; в) более трех изделий.

O. Здесь n = 1000 достаточно велико, а вероятность p = 0,003 – мала, поэтому применим формулу Пуассона. Здесь l = np = 1000·0,03 = 3.

160