Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Пальчик_Теория вероятностей

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 246 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

O. Следует из определений 6.4 и 6.5. Ä.

6.13.3. Если X1 и X2 – независимые СВ, то M (X1 × X2 ) = M (X1) × M (X2 ).

Если X1 и X2 – зависимые СВ, то
M ( X1 × X 2 ) = M ( X1) × M ( X 2 ) + M [( X1 - M ( X1)) × ( X 2 - M ( X 2 ))].	(6.24¢)
Æ. (6.24¢) будет доказано ниже (теорема 10.9.).
6.13.4. Если X1 и X2 – СВ, то
M ( X1 ± X 2 ) = M ( X1) ± M ( X 2 ).	(6.25)

O. По определению 6.4 СВ Х1 + Х2 имеет следующий закон распре- деления:

X1 + X 2

x + x

...

x + x

...

+ x

...

+ x

...

p1 p1

p1 p2

p1 pn

pm p1

pm p2

pm pn

По 6.5. имеем: M(X + X

) = (x + x ) p p + (x + x ) p p

+ K +

+(x + x ) p p + K + (x + x ) p p + (x + x ) p p + K +

1 n

+(x + x ) p p

= x p [ p

+ p

+ K + p

] + p [x p

+ x p

+ K + x p

] + K +

n m n

1 1 1

2 2

n n

+ x p [ p

+ p + K + p ] + p [x p + x p

+K + x p

] =

m m

1 1

2 2

n n

= (x p +K + x p ) ×1 + [x p + x p

+K + x p

] × ( p +K + p ) =

1 1

m m

1 1

2 2

n n

1442443

= 1 по (4.4)

= M(X1 ) +M(X2 ). Ä.

6.13.5.

M(X – M (X)) = 0.

(6.26)

О. По (6.25) M(X – M (X)) = M(X) – M (M(X)) = M(X) –

M(X) (ввиду

(6.16) и 6.13.1) = 0. Ä.

6.13.6. Размерности величин X и M(X) одинаковы.

6.14. Свойства дисперсии.

6.14.1.

D(X) = M(X2) – [ M(X)]2.

(6.27)

О. D(X) = M(X-M(X))2 = M ( X 2 - 2 X × M ( X ) + M ( X )2 ) =

= (6.25) = M ( X 2 ) - M (2 X × M ( X )) + M (M ( X )2 ) =

= по (6.16), 6.13.2, 6.13.1 = M(X2 ) - 2M ( X )M ( X ) + [M ( X )]2 =

= M ( X 2 ) -[M ( X )]2. Ä.

6.14.2. Если C = const, то D(C) = 0.

O. По (6.27) D(C) = M(C2) – M(C)2 = 6.13.1 = C2 – C 2 = 0. Ä. 6.14.3. Если C = const, то D(CX) = C2D(X).

О. D(CX ) = M (C2 X 2 ) - M (CX )2 = C2M ( X 2 ) - C2M ( X )2 =

= C2[M ( X 2 ) - M ( X )2 ] = C2 D( X ). Ä.

6.14.4. Размерность D(X) есть квадрат размерности СВ X.

O. Пусть СВ X измеряется в определенных единицах измерения. То-

гда по 6.14.3 имеем D(X ед) = ед2 D(X). Ä. 6.14.5. D(X – M (X)) = D(X).

О. D(X – M (X)) = M(X – M (X))2 – [M(X – M (X))]2 =

=M(X2 – 2XM(X) +M(X)2) – [M(X) – M (X)]2 =

=M(X2) – 2M(X)M(X)+M(X)2 = M(X2) – M (X)2 = D(X). Ä.

6.14.6.D( X ± Y ) = D( X ) + D(Y ) ± 2M [( X − M ( X ))(Y − M (Y ))].

О. D(X – Y ) = по (6.27) = M(X – Y )2 – [M(X – Y )]2 =

= M(X2 – 2XY + Y2) – [M(X) – M (Y)]2 =

=M(X2) – 2M(XY) + M(Y2) – M (X)2 +2M(X)M(Y) – M (Y)2 =

= по (6.24') = M ( X	2 ) -[M ( X )]2	+ M (Y	2 ) -[M (Y )]2	– 2M (X)M(Y) –
144424443		14424443
	D( X )		D(Y )

– 2M[(X–M (X))(Y–M (Y))]+2M(X)M(Y)=D(X)+D(Y)– 2M[(X–M (X))(Y–MY ))]. Ä.

6.14.7.Следствие. Если C = const, то

D(C ± X) = D(X).

(6.28)

О. D(C – X ) = по 6.14.6 = D(C) + D(X) – 2M[(C – M (C))(X – M (X))] =

=0 + D(X) – 0 = D(X). Ä.

6.14.8.Следствие. Если X и Y – независимые СВ, то

D(X ± Y) = D(X) + D(Y).

(6.29)

O. По 6.14.6

D( X ± Y ) = D( X ) + D(Y ) ± 2M [( X - M ( X )) × (Y - M (Y ))]. Но по 6.13.3

2M[(X-M(X)) × (Y-M(Y))] = 2M(X-M(X)) × M(Y-M(Y)) = (6.26) = 0. Ä.

6.15. Пример. Статистическими наблюдениями замечено, что в сол- нечный день один продавец мороженого продает его » на 160 руб., а в дождливый » на 20 руб. Какова ожидаемая выручка (МО), если вероят- ность, что день будет дождливым, равна 0,35?

О. Пусть СВ X – возможная выручка. Тогда по условию

X	20 pуб.	160 pуб.

P	0,35	0,65

M ( X ) = 20 pуб.× 0,35 +160 pуб.× 0,65 =111 pуб.

Дневная выручка имеет среднее квадратическое отклонение от ожи- даемой


			1
s(X) =		= M(X2) -[M(X)]2 =[(202 ×0,35+1602 ×0,65) -1112]			»67 pуб. Ä.
	D(X)			2

7. Одноточечное распределение. Распределение Бернулли (двухточечное). Биномиальное распределение. Геометрическое распределение. Гипергеометрическое распределение. Нормальное распределение

7.1. Одноточечное распределение. СВ X имеет одноточечное (вы-

рожденное) распределение, если она принимает одно значение х0 с вероят- ностью 100 %, т.е.

F(x) =	0	" x £ x0 ;	(7.1).
	1	" x > x0.

7.2. Распределение Бернулли (двухточечное). СВ X имеет двух-

точечное распределение, если она принимает только 2 возможных значе- ния (например, число появлений события A в одном эксперименте):

X x1	x2		(7.2)
P p1	p2	p1 + p2 =1	(7.2)
P p1	p2	p1 + p2 =1
WX	1	0	(7.2¢)
PX	p	1 - p	(7.2¢)
Распределение такой СВ называется распределением Бернулли. Для
нее имеет место
M ( X ) =1× p + 0 × (1 - p) = p
			(7.2²)
			(7.2²)
D( X ) = M ( X 2 ) - (M ( X ))2 = p - p2 = p(1 - p) = pq
0		x ≤ 0;
F (x) = 1 - p " 0 < x £1;
1		" x >1.

Распределение Бернулли (7.2¢) является математической моделью любого вероятностного эксперимента Е с двумя исходами WX = {0; 1}.

Играет важную роль в ТВ и МС.

7.3. Биномиальное распределение. Пусть Е проводится n раз.

Каждое повторение эксперимента Е может закончиться появлением неко- торого события А, либо не появлением А. При этом Р(А) пусть одна и та же при каждом повторе эксперимента.

Свяжем с n-кратным повторением Е СВ Х – число появлений А в се- рии из n повторов E.

Как вычислить при этих условиях P(X = k)?	(7.3)
Для этого X представим в виде суммы n независимых	СВ:

X = ∑ Xi , где Xi – число появлений A в единичном эксперименте.

i=1

Вединичном (отдельном) эксперименте Xi может принять только 2 значения: 1 и 0. То есть Xi имеет двухточечное распределение Бернулли.

W(Xi) = {0, 1}, P(Xi = 1) = p, P(Xi = 0) = q = 1 – p.

Нас интересует вопрос (7.3). Ответ на этот вопрос мы рассмотрели в лекции 5 (см.(5.2).

Так как имеются формулы (7.2²), то для биномиально распределен- ной СВ X имеем:

n
M ( X ) = M (∑ Xi ) = n × p
i=1		(7.3¢)
n		(7.3¢)
n
D( X ) = D(∑ Xi ) = n p q
D( X ) = D(∑ Xi ) = n p q
i=1

Пример. Прибор состоит из 10 узлов. Надежность каждого узла в течение времени t равна 0,95. Узлы могут выходить из строя независимо друг от друга. Найти вероятность того, что за время t

1)откажут точно 2 узла (С);

2)откажут не менее 2-х узлов (D).

O. Пусть X – число узлов, отказавших за время t. Тогда

WX = {xi / i = 0,10} = {0,1, K, 10}.

P( X = xi ) = Cnxi pxi qn− xi ( p = 0,05; q = 0,95).

C= {2}; (СВ X примет значение, равное 2);

D= {2, 3, ..., 10} (СВ X примет значение 2,...,10).

P(C) = P( X = 2) = C102 p2q8 = 45 × 0,052 × 0,958 = 0,075.

10		0,05xi × 0,9510− xi = 0,086.	Ä.
P(D) = P( X ³ 2) = ∑ C xi
xi =	10
	2

7.4. Геометрическое распределение. Пусть производится n неза-

висимых опытов, в каждом из которых A может появиться с вероятностью p = const. Поставим вопрос не так, как в (7.3), а таким образом: «В каком опыте наступит A первый раз?»

В таком случае рассматриваем СВ X – число экспериментов (в схеме Бернулли) до наступления события A первый раз.

Очевидно, A появится первый раз в i-м опыте, если первые (i – 1) опытов закончились неудачно для A (что произойдет с вероятностью (1 - p)i-1) и i-й опыт закончится успехом, т.е. A наступит (что произойдет с вероятностью p). Итак,

%	i−1	(7.4)
P( X = i) = p × q	,	(7.4)

где X – СВ, выражающая число экспериментов, в которых А появилось

1-й раз в i-м опыте.

∞

× qi−1. Это есть геометрическая прогрессия со

Рассмотрим ряд ∑ p1

i=1

∞

знаменателем q, |q| < 1. Поэтому ∑ p qi−1 = p(

) = p × (1/ p) =1. Но это

i=1

- q

означает, что формула (7.4) задает распределение СВ X. Его называют

геометрическим.

+K+ ipq

i−1

+K =

M ( X ) =1× p + 2 pq + 3 pq

= (1 - q) + 2(q - q2 ) +K+ i(qi−1 - qi ) +K =

(7.4¢)

=1 + q + q2 +K+ qi −1 - iqi +K =

+ 0 =1/ p.

- q

Аналогично,

1 − p

D( X ) =

(7.4²)

7.5. Гипергеометрическое распределение. С помощью гипергео-

метрического распределения вычисляется доля бракованных деталей в выборке из контролируемой партии.

Пусть в контролируемой партии имеется N деталей, из них M брако- ванных и N – M стандартных. Из этой партии взято наугад n деталей. СВ X – число бракованных деталей среди n взятых.

Пусть бракованных деталей среди взятых m штук.

Число всевозможных партий из n деталей равно CNn . Среди них име- ется CMm CNn−−mM партий, содержащих m бракованных деталей. По классиче- скому определению вероятности события (X = m) имеем

	m n−m
P( X = m) =	CM CN −M			.	(7.5)
P( X = m) =	CNn			.	(7.5)
	CNn
Можно показать, что
M ( X ) = n p;
		n −1			(7.5′)
D( X ) = npq(1 −		n −1			(7.5′)
			)
		N −1	)
		N −1

7.6. Определение. Нормальным называется такой закон распреде- ления НСВ X, который описывается дифференциальной функцией распре- деления (т.е. плотностью вероятности)

1				−	(n−m)2
					2σ2

f (x) =	s		× e			.	(7.6)
		2p

Выясним вероятностный смысл параметров m и s в (7.6). Если они известны, то известна и f(x). Для этого вычислим M(X) и D(X). Получаем

∞

−

(n−m)2

2σ2

M ( X ) = ∫ x f (x) dx =

∫

x × e

dx =

−∞

s 2p −∞

x - m

= z; x

= sx + m

∞

∫ (s z +m) e− z2 / 2s × dz =

dx = sdz

−∞

∞

2 / 2 z dz +

∞

e− z2 / 2dz = 0 +

∫ se− z

= m.

∫

2p −∞

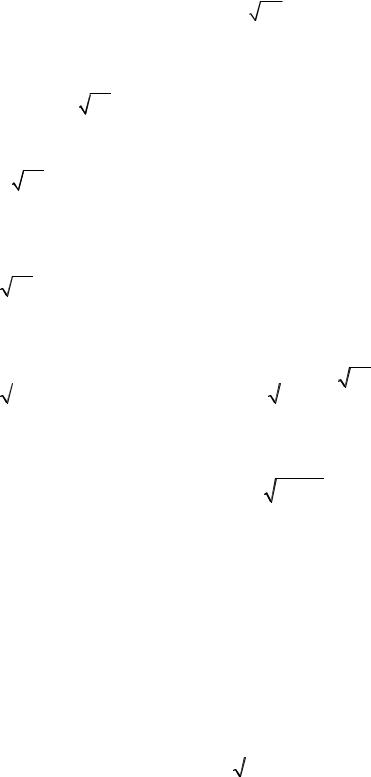
Первый интеграл равен 0, т.к. под знаком интеграла стоит нечетная функция, а границы интервала симметричны относительно начала коорди- нат. Второй интеграл есть «не берущийся» интеграл Пуассона, его вычис-

ляют специальным приемом; он равен 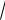2p .

∞

(n−m)2

(x - m)2 e 2σ2 dx =

D( X ) = ∫

−∞ s

∞

∫ z2 × s2 × e− z2 / 2 × s × dz (здесь, как и выше, x – m = s z) =

2p −∞

∞

u = z, du = dz

∫ z × e− z2 / 2 × z × dz =

dv = e− z2

/ 2 × z × dz = -e− z2 / 2d (-

)

−∞

v = -e− z2 / 2

∞

− z

2 / 2

∞

− z2 / 2

(-z × e

−∞

+ ∫ e

dz) =

(0 +

2p) = s

−∞

Итак, в (7.6) имеем

m = M ( X ), s =

D( X ).

(7.7)

Из (7.7) и вытекает вероятностный смысл параметров m и s нор- мального распределения.

Если m и s – произвольные числа, то (7.6) называют общим нор- мальным распределением, а если

m = 0, s = 1,

то (7.6) называют нормированным (или стандартным) законом нормально- го распределения:

f0	(x) =	1	× e− x2 / 2.	(7.8)

		2p

Условимся писать, что X Î N(m, s), если X имеет распределение

(7.6).

Соответственно для (7.6) и (7.8) могут быть найдены интегральные функции распределения.

А именно, по (4.12) имеем:

(t −m)2

F (x) =

∫ ×e 2σ2 dt,

(7.9)

2p −∞

F0 (x) =

∫ ×e−t2 / 2 dt = F (x).

(7.10)

2p −∞

Обозначение Ф*(x) для F0(x) связано с обозначением Ф(x)

рассмотренной в лекции 5 функции Лапласа:

2 / 2 dt.

F(x) =

∫×e−t

(7.11)

Для функций Ф(x) и Ф*(x) имеются специальные таблицы их при- ближенных значений, так как они часто используются в ТВ и МС.

Ф*(x) называют нормальной функцией распределения (Лапласа).

Функции F(x), F0(x)= Ф*(x) и Ф(x) связаны между собой следующи- ми соотношениями:

	x − m						x − m
F (x) = F (				) = F		(			) ;	(7.12)
F (x) = F (		s		) = F		(		s	) ;	(7.12)
0		s						s
0
F (x) =		1	+ F(		x − m			).		(7.13)
F (x) =			+ F(					).		(7.13)
	2				s

В самом деле,

−

(t −m)2

t - m

= z, t = sz + m, dt = sdz

F (x) =

×e

2σ2

dt =

∫

x - m

2p −∞

-¥ < t < x Û -¥ < z <

1× s

( x−m) / σ

∫ ×e− z2 / 2dz =

∫

×e− z2 / 2dz = F0 (

x - m

) .

s 2p

−∞

Выражение (7.12) доказано.

Далее,

( x−m) / σ

×e− z2

×e− z2 / z dz +

( x−m) / σ

2 / 2dz =

F (x) =

∫

/ z dz =

∫

∫ ×e− z

−∞

2p −∞

−∞

2 / 2dz +

( x−m) / σ

2 / 2dz = -F(-¥) + F(

x - m

= -

∫ ×e− z

∫

×e− z

) =

= F(¥) + F(

x − m

) =

+ F(

x − m

) и (7.13) доказано.

7.7.Теорема. Если X ÎN(m, s), то

β − m

α − m

) = F(

β − m

) - F(

α − m

) (7.14)

P(a £ X < b) = F (

) - F (

О. По (4.5) P(a ≤ X <b) = F(b) – F (a) = (7.13) =

+ F(

β − m ) -

- F(

α − m ) = F(β − m ) - F(α − m ).

Использование (7.12) дает остальное. Ä.

7.8.Теорема. Пусть X Î N(m, s), d Î R. Тогда

P(| X - m |< d) = 2F(

(7.15)

О. P(|X – m| < d) = P(– d + m < X < m + d) = (7.14) =

= F(

m + δ − m

) - F(

m − δ − m

) = F(

) - F(-

) = 2F(

). Ä.

7.9.Правило «трех сигм». Если X Î N(m, s) и d = 3s, то

P(\|X – m\| < 3s) » 1.	(7.16)
O. По (7.15) P(\|X – m\| < 3s)= 2 × Ф(3) » 2 × 0,49865 » 1.	Ä.

Из формулы (7.16) следует, что интервал ]m - 3s; m + 3s[ есть ин- тервал практически всех возможных значений СВ X Î N(m, s), так как с увеличением интервала вероятность хотя и возрастет, но незначительно.

<<< < Предыдущая 1 2 3 4 56 / 246 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб48умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб39умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб37умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб43умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб44умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб50умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб42умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб90умк_Яско_ Диф.уравнения_Ряды.pdf