14-es_1 / Высшая математика (РТФ) / умк_Пальчик_Теория вероятностей
.pdfO.
а). здесь СВ Х – время прихода пассажира на остановку от момента ухода предыдущего автобуса до момента прибытия следующего, т.е. СВ Х может принимать значения из интервала [0; 8] и имеет равномерное рас- пределение. Плотность вероятности имеет вид:
f (x) = |
|
1 |
= |
1 |
. |
|
− 0 |
|
|||
8 |
8 |
|
|||
Из данного отрезка выберем те промежутки, куда должна попасть СВ Х, чтобы выполнялось условие задачи: [2; 8 – 3] = [2; 5]. Т.о.:
5 |
5 |
1 |
|
1 |
|
|
|
|
5 − 2 |
|
3 |
|
|
P(2 ≤ x ≤ 5) = ∫ f (x)dx = ∫ |
dx = |
x |
|
52 |
= |
= |
; |
||||||
|
|||||||||||||
|
|
|
|
||||||||||
8 |
8 |
|
8 |
8 |
|
||||||||
2 |
2 |
|
|
|
|
||||||||
б) для того, чтобы выполнялось условие данного пункта, надо, чтобы СВ Х попала в интервал [4; 8], т.о.:
8 |
1 |
|
1 |
|
|
|
|
4 |
|
1 |
|
|
P(4 ≤ x ≤ 8) = ∫ |
dx = |
x |
|
84 |
= |
= |
. |
|||||
|
||||||||||||
|
|
|
|
|||||||||
8 |
8 |
|
8 |
2 |
|
|||||||
4 |
|
|
|
|
||||||||
Ответ: а) 3/8; б) 1/2.
8.4. Пример. Минутная стрелка часов перемещается скачками в кон- це каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 10 се- кунд.
O. СВ Х – истинное время (в течение текущей минуты), имеет рав- номерное распределение.
СВ Х может принимать значения из интервала [0; 60]. |
|
|
|||||||||||
f (x) = |
|
1 |
|
= |
1 |
. |
|
|
|
|
|
|
|
60 − 0 |
|
|
|
|
|
|
|
||||||
|
60 |
|
|
|
|
|
|
|
|||||
Погрешность не превысит 10 секунд, если СВ Х примет значения из |
|||||||||||||
интервалов [0; 10] или [50; 60]. Т.о.: |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
1 |
|
60 |
1 |
|
1 |
|
1 |
|
|||
P(0 ≤ x ≤ 10) + P(50 ≤ x ≤ 60) = ∫ |
|
dx + ∫ |
dx = |
(10 + 10) = |
. |
||||||||
60 |
60 |
60 |
|
||||||||||
0 |
|
50 |
|
|
3 |
||||||||
|
|
|
|
|
|
|
|
|
|||||
Ответ: 1/3.
171
8.5. Пример. Среднее время ожидания у бензоколонки автозапра- вочной станции равно 5-ти минутам. Найти закон распределения СВ Х –
время ожидания, F(x), D(x), P(1 ≤ x ≤ 3 ).
O. СВ Х имеет показательное (экспоненциальное) распределение. В данном случае l = 5. Закон распределения (плотность вероятности) имеет вид:
|
0, |
x < 0; |
||
|
|
|
|
|
f (x) = |
|
|
|
|
|
5e-5x , x ³ 0. |
|||
F (x) =1 - e−5x , |
при x ³ 0 . |
|||
D(x) = |
1 |
= |
1 |
= 0,04. |
l2 |
|
|||
|
25 |
|
||
P(1<x<3) = F(3) – F(1) = e-5×1 - e-5×3 » 0,00659.
8.6. Пример. Среднее время безотказной работы телевизора равно 3-м годам. СВ Х – время безотказной работы телевизора. Найти P(x < 4).
O. Здесь λ = 3, a = 0, b = 3. Тогда
P(0 £ x £ 3) = e-3×0 - e-3×3 = e0 - e-9 » 1 – 0,00012 = 0,99988.
Задачи для самостоятельного решения
1.Задана плотность распределения вероятностей:
0, |
при x <1, x > 2; |
f (x) = |
при1 £ x £ 2. |
x + a, |
Найти а) константу a, б) M(x), D(x), P(1,5 ≤ x ≤3).
Ответ: а = – 0,5; М(х) » 1,583, D(x) » 0,076, P(1,5 ≤ x ≤3) = 0,357.
2. Цена деления шкалы амперметра равна 0,2. Показания округляют- ся до ближайшего целого деления. Найти вероятность того, что при отсче- те будет сделана ошибка, превышающая 0,004.
Ответ: 0,6.
172
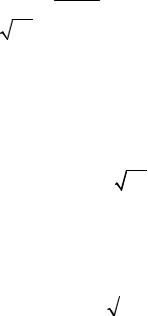
Для нормального распределения также верны формулы (лекция 7,
(7.15), (7.16): |
|
|
|
|
|
|
|
|||
P( |
|
x - m |
|
< d) = 2F(δ |
s |
) , P( |
|
x - m |
|
< 3s) »1 (правило «трех сигм»). |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Значительное число экономических показателей – доход, потребле- |
||||||||||
ние, прибыль фирм в отрасли и т.д. в реальности имеют распределение,
близкое к нормальному распределению.
9.1. Пример. СВ Х подчинена нормальному закону распределения с математическим ожиданием, равным 2, и дисперсией, равной 9. Записать выражение для плотности вероятности и найти вероятность того, что СВ Х
примет значения из интервала [1; 4].
O. Для данной СВ Х параметр m = 2, s = 
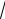D = 
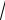9 = 3 , тогда плот-
ность распределения имеет вид:
|
1 |
|
|
− |
( x−2)2 |
|
|
f (x) = |
|
|
|
|
|||
|
|
|
e |
18 |
. |
||
3 |
|
|
|
|
|||
2p |
|
|
|||||
P(1 £ x £ 4) = F( 4 − 2) - F(1 − 2) = F(0,67) - F(-0,33) » 3 3
» 0, 2486 + 0,1293 = 0,3779
(здесь учли, что Ф(– х)= – Ф(х)).
Ответ: 0,3779.
9.2. Пример. Плотность вероятности СВ Х задана выражением:
f (x) = ae |
− |
( x−5)2 |
. |
|
|||
8 |
|||
|
|
||
Найти коэффициент а и определить вероятность того, что в результа-
те опыта СВ Х отклонится от своего математического ожидания не более,
чем на 1,5.
O. Учитывая вид плотности вероятности нормального распределе-
ния, имеем: m = 5, 2σ2 = 8, σ = 2, тогда, т.к. а = 1/(σ
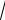2p ), то a =1/(2
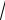2p) » 0, 2 .
P( x - m <1,5) = 2F(1,5) = 2F(0,75) = 2 × 0,2734 = 0,5468 . 2
Ответ: 0,2; 0,5468.
174
9.3. Пример. Автомат изготовляет детали, которые считаются год- ными, если отклонение их размера от проектного по модулю не превосхо- дит 0,77 мм. Каково наиболее вероятное число годных среди ста деталей, если СВ Х – отклонение размера детали от проектного распределена нор- мально со стандартным (средним квадратическим) отклонением, равным
0,4 мм?
O. Найдем вероятность появления годной детали.
P( x < 0,77) = 2F( 0,770,4 ) = 2F(1,925) = 0,9464 .
Число годных деталей среди 100 взятых с известной вероятностью появления одной годной детали p = 0,9464 – это ДСВ Y, имеющая биноми- альное распределение. Тогда k – наивероятнейшее число появления собы- тия (число годных деталей) при 100 испытаниях равно:
np – q ≤ k ≤ np + p.
n = 100; q = 1 – 0,9464 = 0,0536; 100 ·0,9464 – 0,0536 ≤ k ≤ 100·0,9464 + 0,9464.
94,5864 ≤ k ≤ 95,5864; т.к. k – целое число, то k = 95.
Ответ: 95.
9.4. Пример. Случайное отклонение Х размера детали от номинала распределено по нормальному закону со средним квадратическим откло- нением, равным 5 мк, систематические ошибки отсутствуют. Каким дол- жен быть допуск, чтобы с вероятностью не более 0,0027 получилась деталь
сконтролируемым размером вне поля допуска?
O. Т.к. систематические ошибки отсутствуют, т.е. отсутствуют ошибки одного знака, значит математическое ожидание СВ Х m = 0; σ = 5.
P( |
|
x |
|
> d) £ 0,0027, |
- P( |
|
|
|
x |
|
> d) ³ -0,0027, |
1 - P( |
|
x |
|
> d) ³1 - 0,0027. |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
1 - P( |
|
x |
|
> d) = P( |
|
x |
|
£ d) = 2F(δ |
s |
), |
1 - 0,0027 = 0,9973, |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
т.о., 2F(δ |
s |
) ³ 0,9973, |
F(δ |
) ³ 0, 49865, |
F(x) = 0,49865, x = 3, |
||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||||
т.е. δ/5 ≥ 3, следовательно, δ ≥ 15. Ответ: не менее 15-ти.
175
9.5. Пример. Из пункта С ведется стрельба из орудия вдоль прямой СК. Предполагается, что СВ Х – дальность полета снаряда распределена нормально с математическим ожиданием 1000 м и средним квадратиче- ским отклонением 5 м. Определить (в %), сколько снарядов упадет с пере- летом от 5 до 70 м.
O. Здесь m = 1000, σ = 5. Найдем P(1005 ≤ x ≤1070):
P(1005 ≤ x ≤1070) = Ф((1070 – 1000)/5) – |
Ф((1005 – 1000)/5) = Ф(70/5) – Ф(5/5) = |
= Ф(14) – Ф(1) = 0,5 – 0,3413 = 0,1587, |
т.к. для всех x > 5 Ф(х) = 0,5. |
Т.о. определили, что 15,87 % снарядов упадет с перелетом от 5 до 70 м.
Ответ: 15,87 %.
9.6. Пример. Производят взвешивание вещества. Случайная ошибка взвешивания распределена нормально с математическим ожиданием 10 кг и средним квадратическим отклонением 2 кг. Найти вероятность того, что следующее взвешивание отличается от математического ожидания не бо- лее чем на 100 г.
О. Здесь m = 10, σ = 2, 100 г = 0,1 кг.
P( x - m £ 0,1) = 2F(0,1) = 2F(0,05) = 2 × 0,01994 = 0,0398 . 2
Ответ: 0,0398.
10. Двумерные СВ (Х, Y).
Условные законы распределения компонент X и Y
Совместное распределение двух СВ X и Y приводит к системе слу- чайных величин; распределение системы двух случайных величин может быть задано в виде таблицы (лекция 9, (9.3.):
|
Y/X |
|
x1 |
|
x2 |
… |
x |
n |
|
y1 |
|
p11 |
|
p21 |
… |
p |
n1 |
|
y2 |
|
p12 |
|
p22 |
… |
p |
n2 |
|
… |
… |
|
… |
… |
… |
|
|
|
|
|
|
|
|
|
|
|
|
ym |
|
p1m |
|
p2m |
… |
p nm |
|
P(X = xi, Y = yj) = pij. i = 1…n; j = |
1…m. |
n m |
= 1. |
|
||||
∑ ∑ pij |
|
|||||||
i=1 j =1
176
Маргинальное |
распределение |
компоненты |
Х (при i = 1… n): |
|||||||
m |
|
|
|
|
|
|
|
|
|
|
P( X = xi ) = ∑ pij (формула (9.5). Маргинальное распределение компонен- |
||||||||||
j =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
ты Y (при j = 1… m): P(Y = yj) = ∑ pij |
(формула (9.6.). |
|
||||||||
|
|
i=1 |
|
|
|
|
|
|
|
|
Математические ожидания СВ Х и СВ Y: |
|
|
|
|
||||||
M = |
n m |
|
|
m |
y |
|
m |
p |
. |
|
x |
p , M = |
∑ |
∑ |
|||||||
x |
|
∑ i ∑ |
ij |
y |
|
j |
ij |
|
||
|
|
i=1 j =1 |
|
|
j =1 |
|
i=1 |
|
|
|
Дисперсии: |
|
|
|
|
|
|
|
|
|
|
n |
|
m |
|
|
m |
|
n |
|
|
|
Dx = ∑xi2 ( ∑ pij ) − M x2 ; Dy = ∑ y2j (∑ pij ) − M y2 . |
||||||||||
i =1 |
|
j =1 |
|
|
j =1 |
|
i=1 |
|
||
Средние квадратические отклонения:
σx = 
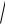Dx , σ 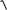y = 
Dy .
Корреляционный момент (ковариация) (формула 9.32):
n m |
− M x )( y j |
− M y ) pij |
|
|
n m |
− M xM y . |
||
Kxy = ∑ ∑ (xi |
= ∑ ∑ xi y j pij |
|||||||
i=1 j =1 |
|
|
|
|
|
|
i =1 j =1 |
|
Коэффициент корреляции: |
|
|
|
|
|
|
|
|
|
ρxy = |
K xy |
, |
|
ρ |
|
≤ 1. |
|
|
|
|
|
|||||
|
|
|
||||||
|
|
σxσ y |
|
|
|
|
|
|
Для условного распределения составляющей Х при условии, что со- ставляющая Y принимает значения yj (и условного распределения состав- ляющей Y при условии, что составляющая X принимает значения xi), будем пользоваться формулами:
P(x / y |
j |
) = |
P(xi y j ) |
, |
P( y |
j |
/ x ) = |
P(xi y j ) |
. |
|
|
||||||||
i |
|
P( y j ) |
|
|
i |
P(xi ) |
|||
|
|
|
|
|
|
|
|||
177
10.1. Пример. Распределение системы СВ (Х, Y) задано таблицей:
Y/X |
0 |
1 |
2 |
3 |
|
|
|
|
|
– 1 |
0,01 |
0,06 |
0,05 |
0,04 |
|
|
|
|
|
1 |
0,04 |
0,24 |
0,15 |
0,07 |
|
|
|
|
|
2 |
0,05 |
0,10 |
0,10 |
0,09 |
|
|
|
|
|
Найти 1) маргинальные законы распределения СВ Х и СВ Y; 2) их математические ожидания и дисперсии; 3) коэффициент корреляции меж- ду Х и Y; 4) закон распределения составляющей Х, если составляющая Y = 1; 5) закон распределения составляющей Y, если составляющая Х = 2; 6) условное математическое ожидание составляющей Х при условии, что
Y = 1.
O.
1) P(X = 0) = 0,01 + 0,04 + 0,05 = 0,1; P(X = 1) = 0,06 + 0,24 + 0,10 = 0,4; P(X = 2) = 0,05 + 0,15 + 0,10 = 0,3; P(X = 3) = 0,04 + 0,07 + 0,09 = 0,2.
Маргинальный закон распределения СВ Х имеет вид:
X |
0 |
1 |
2 |
3 |
|
|
|
|
|
Px |
0,1 |
0,4 |
0,3 |
0,2 |
P(Y = – 1) = 0,01 + 0,06 + 0,05 + 0,04 = 0,16; P(Y = 1) = 0,04 + 0,24 + 0,15 + 0,07 = 0,5; P(Y = 2) = 0,05 + 0,10 + 0,10 + 0,09 = 0,34.
Маргинальный закон распределения СВ Y имеет вид:
Y |
–1 |
1 |
2 |
|
|
|
|
Py |
0,16 |
0,5 |
0,34 |
2) используя маргинальные законы распределения СВ Х и СВ Y, най- дем их числовые характеристики:
Mx = 0·0,1 + 1·0,4 + 2·0,3 + 3·0,2 = 1,6; My = –1 ·0,16 + 1·0,5 + 2·0,34 = 1,02;
Dx = 02·0,1 + 12·0,4 + 22·0,3 + 32·0,2 – (1,6) 2 = 0,84; σx = 
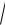Dx = 0,9165 ;
Dy = (– 1) 2·0,16 + 12·0,5 + 22·0,34 – (1,02) 2 = 0,2876; σy = 
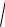Dy = 0,5363;
3) для нахождения коэффициента корреляции вычислим прежде ко- вариацию:
178
Kxy = 0((– 1) ·0,01 + 1·0,04 + 2·0,05) + 1((– 1) ·0,06 + 1·0,24 + 2·0,10) + 2((– 1) ·0,05+ +1·0,15 + 2·0,10) + 3((– 1) 0,04 + 1 ·0,07 + 2·0,09) – (1,6)(1,02) = – 0,022.
Т.о. коэффициент корреляции равен: rxy |
= |
−0,022 |
» 0,045 ; |
||
0,9165 |
× 0,5363 |
||||
|
|
|
|||
4) найдем закон распределения составляющей Х при условии, что
Y = 1.
P(X = 0/Y = 1) = 0,04/0,5 = 0,08; P(X = 1/Y = 1) = 0,24/0,5 = 0,48; P(X = 2/Y = 1) = 0,15/0,5 = 0,3; P(X = 3/Y = 1) = 0,07/0,5 = 0,14.
Т.о. условный закон распределения СВ Х при Y = 1 имеет вид:
X |
0 |
2 |
2 |
3 |
|
|
|
|
|
P(X/Y = 1) |
0,08 |
0,48 |
0,3 |
0,14 |
|
|
|
|
|
5) найдем закон распределения составляющей Y при условии, что
Х = 2.
P(Y = –1/ X = 2) = 0,05/0,3 = 0,167; P(Y = 1/X = 2) = 0,05/0,3 = 0,5; P(Y = 2/X = 2) = 0,1/0,3 = 0,33.
Условный закон распределения СВ Y при Х = 2 имеет вид:
|
Y |
|
|
– 1 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(Y/X = 2) |
|
0,167 |
|
0,5 |
|
0,333 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
6) условное математическое ожидание вычислим по формуле (9.28): |
|||||||||||||||
4 |
|
|
|
|
0,04 |
|
0, 24 |
|
0,15 |
|
0,07 |
|
|||
M ( X /Y =1) = ∑x p(x /Y = y |
|
=1) = 0 × |
+1× |
+ 2 × |
+ 3 × |
= |
|||||||||
2 |
|
|
|
|
|||||||||||
i i |
|
|
0,5 |
|
0,5 |
|
0,5 |
0,5 |
|
||||||
i=1 |
|
|
|
|
|
|
|||||||||
= 0+0,48+0,6+0,42 = 1,5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дополнительные задания по законам распределения ДСВ
Найти закон распределения СВ Х, F(x), M(x), D(x).
1.Вероятность того, что покупателю потребуется обувь 40-го разме- ра, равна 0,4. В обувной отдел вошли 7 покупателей. СВ Х – число покупа- телей, которым потребовалась обувь 40-го размера. P(3 < x < 6) = ?
2.В ячейку памяти ЭВМ записывается 8-ми разрядное двоичное чис- ло. Значения 0 и 1 в каждом разряде появляются с равной вероятностью. СВ Х – число единиц в записи двоичного числа. P(3 < x < 6) = ?
179
3.Вероятность работы каждого из 8-ми комбайнов без поломок в те- чение определенного времени равна 0,9. СВ Х – число комбайнов, рабо- тавших безотказно в течение данного времени. P(2 < x < 4) = ?
4.Вероятность того, что покупатель совершит покупку в данном ма- газине, равна 0,4. СВ Х – число покупателей, совершивших покупку в дан- ном магазине. P(2 < x <5) = ?
5.В некотором цехе брак составляет 5 % всех изделий. СВ Х – число бракованных изделий среди 8-ми взятых. P(4 < x <8) = ?
6.Вероятность поражения мишени при одном выстреле равна 0,6. СВ Х – число поражений мишени при 7-ми выстрелах. P(x >4) = ?
7.Вероятность выпуска прибора, удовлетворяющего требованиям качества, равна 0,7. В контрольной партии 8 приборов. СВ Х – число при- боров в партии, удовлетворяющих требованиям качества. P(3 < x <6) =?
8.Вероятность сдачи данного экзамена для каждого из 9-ти студен- тов равна 0,8. СВ Х – число студентов, сдавших экзамен. P(6 < x <9) = ?
9.В партии из 20-ти телефонных аппаратов 4 неисправных. СВ Х – число неисправных аппаратов среди 6-ти случайным образом отобранных.
P(3 < x < 6) = ?
10.90 % панелей, изготовляемых на железобетонном заводе – выс- шего сорта. СВ Х – число панелей высшего сорта из 7-ми, взятых наугад.
P(x > 4) = ?
11.Производятся последовательные испытания 8-ми приборов на надежность. Каждый следующий испытывается только в том случае, если предыдущий оказался надежным. Вероятность выдержать испытание для каждого прибора равна 0,4. СВ Х – номер испытания, на котором заканчи- вается проверка. P(4 < x < 7) = ?
12.Вероятность изготовления нестандартной детали равна 0,1. Из партии контролер берет деталь и проверяет ее качество. Если она оказыва- ется нестандартной, дальнейшие испытания прекращаются, а партия за- держивается. Если деталь окажется стандартной, то контролер берет сле- дующую и т.д. Но всего он проверяет не больше 7-ми деталей. СВ Х – чис- ло проверенных стандартных деталей. P(3 < x <6) = ?
13.На контроль поступила партия деталей из цеха. Известно, что 5 % всех деталей не удовлетворяют стандарту. Берут наудачу 4 детали. СВ Х – число нестандартных деталей среди взятых. P(1 < x < 4) = ?
14.Для сборки прибора требуется 4 детали. Всего имеется 10 дета- лей, из которых только 6 доброкачественных. СВ Х – число доброкачест- венных деталей, взятых из сборки. P(2 < x <4) = ?
180