14-es_1 / Высшая математика (РТФ) / умк_Пальчик_Теория вероятностей

5. ОПГ есть интервал ]– 1,645; ¥[.

6. Считаем партию лампочек не удовлетворяющей условию гаран- тии, если Kнабл. Ï ОПГ.

7. По выборке в 25 лампочек имеем:Kнабл.= 750 − 800 = – 2,083 < – 1,645. 24

Решение: партия лампочек должна быть забракована. Это статисти-

ческое решение верно в 1 – a = 95 % случаев. Ä.

18. Гипотезы о математическом ожидании нормального распределения:

гипотеза о математическом ожидании СВ X N(m, σ),

σ – известная величина;

гипотеза о математическом ожидании СВ X N(m, σ),

σ– неизвестная величина

Влекции 18 мы рассмотрим несколько конкретных критериев К для проверки гипотез о параметрах нормального распределения, так как это распределение является наиболее распространенным в силу ЦПТЛ (см. теоремы 8.10 и 8.11). К тому же следует отметить, что проверка гипотез о параметрах произвольных законов распределения связана с большими математическими трудностями.

Пусть

Пусть m0 – действительное число. Выдвигаем гипотезу H0: m = m0.

Формулируем альтернативную гипотезу Ha: m = m1 ¹ m0.

Наша задача состоит в том, чтобы проверить гипотезу H0 при альтернативной гипотезе Ha: m = m ¹ m0.

Согласно схеме 17.14 нам нужно подобрать подходящий критерий для проверки СГ H0. Подбор критерия удобно сделать в зависимости от того, известна величина s или нет. Рассмотрим отдельно два случая.

18.1. s – известная величина

В связи с соображениями пункта 17.4 в качестве критерия можно взять нормированную СВ

где n – объем выборки (18.2). Кроме того, известен закон распределения СВ и. В самом деле, как показано в (10.22), u Î N(0, 1).

Далее пусть задан уровень значимости a. При «разрешенной» величине a ошибки 1-го рода (отклонить верную гипотезу H0) крити- ческая область, минимизирующая вероятность ошибки 2-го рода, опре- деляется в зависимости от значения m1.

Как отмечено в лекции 17, критическая область (и критические точ- ки) находится исходя из соображения, что

вероятность события и Î KO должна быть равна a (® 0). (18.4)

Рассмотрим сначала случай, когда Hа задается не однозначно,

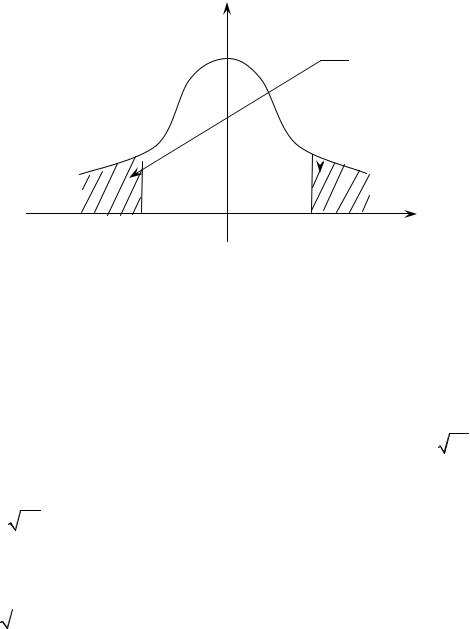
этому кривая f(u) симметрична относительно оси ординат. Поэтому ввиду (18.4) КО ищем как множество значений u, удовлетворяющих неравенству |u| ³ uα (рис. 18.1).

2

132

f (u )

KO

метрии тогда левая критическая точка есть (−uα / 2 ) .

Но можно провести аналогичные рассуждения и найти левую кри- тическую точку по правилу

18.2. Пример. Из нормальной ГС с известным средним квадратиче- ским отклонением s = 0,36 извлечена выборка объема n = 36 и по ней найдена выборочная средняя x = 21,6. Требуется при уровне значимости 0,05 проверить основную гипотезу H0: т = m0 = 21, при конкурирующей ги- потезе На: т ¹ 21.

О. По формуле (18.3) находим наблюдаемое значение критерия

Так как На имеет вид m ¹ m0, то КО – двусторонняя. Правую крити- ческую точку находим по формуле (18.5).

F * (uкр.) =1 - 0,05 = 0,975.

2

По таблице значений функции Ф*(и) находим икр = 1,96. Так как инабл.= 10 > икр =1,96, то и Î КО и по 17.8 гипотезу

H0 : т = 21 отвергаем. Ä.

Рассмотрим теперь случай, когда Hа задается однозначно.

Пусть На: т = m1 > m0. В этом случае КО должна быть односторонней с со- блюдением принципа (18.4.).

Возникает вопрос: КО должна быть левосторонней или право- сторонней?

Для ответа на этот вопрос можно рекомендовать следующее соображе- ние. Подставим в формулу (18.3) вместо m сначала m0, затем m1 > m0. Получим, что u(m0) > u(m1), то есть, чтобы отклонить H0 (u Î КО), нужно, чтобы uнабл. превзошло некоторое подходящее значение критерия и = икр. То есть критическая область должна быть правосторонней. Ввиду (18.4) (и (17.6) имеем:

Из равенства (18.6) и находим правую критическую точку uкp.

134

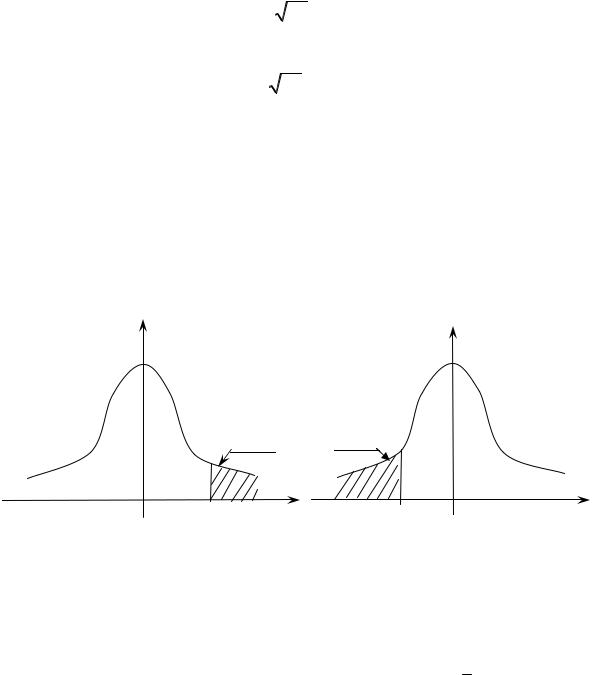
Аналогичные рассуждения для случая, когда альтернативная гипотеза имеет вид Ha: m = m1 < m0, приводят нас к левосторонней КО:

Зная α, по таблицам значений функции Лапласа Ф*(и) находим левую критическую точку (– икр).

Обе последние ситуации изображены на рис. 18.2.

18.3. Пример. На станке-автомате штампуется деталь с контроли- руемым размером m = 12 мм. Известно, что распределение контролируемого размера является нормальным: X N(m; 0,5). ОТК за смену измерил 36 слу-

чайно отобранных деталей и подсчитал средний размер x = 11,7 мм кон- тролируемого параметра.

Можно ли утверждать с вероятностью 95 %, что станок-автомат изго- тавливает детали уменьшенного размера и нужно делать его переналадку?

О. Проверим основную гипотезу H0 : т = 12 мм против альтернатив-

135

ной гипотезы На : т < 12 мм. По предположению ОТК Нα: т = m1 < 12 мм и поэтому применяем критерий (18.3) с левосторонней КО (см. рис. 18.2, б). То есть, отклоним гипотезу H0, если

квантиль стандартизированного нормального распределения, удовлетво- ряющий условиям (18.7) и (18.8). Р(и ≤ – u 0,05) = 0,05. По таблицам значений Ф*(u) находим, что – u = – 1,64.

Так как инабл. = – 3,6 < – 1,64 = – ихр, то значение и попадает в левую КО, а не в ОПГ H0. По принципу 16.8 H0 отклоняется в пользу Hа. Это означает, что с вероятностью 95 % можно утверждать, что станок делает детали с уменьшенным контролируемым размером и требуется переналад- ка станка. Ä.

18.4. s – неизвестная величина

Наиболее трудньй пункт в схеме 17.14 есть пункт 17.14.2. Для его осуществления нужно знать подходящий спектр СВ с известными распре- делениями (в соответствии с 17.14). Из этого набора СВ и можно вы- брать такую, которая может быть использована в качестве критерия К для проверки СГ.

Например, из теоремы 14.5 следует, что в качестве критерия К можно взять СВ

ки (18.2).

Согласно теореме 14.5 Т распределена по закону Стьюдента с п – 1 степенями свободы.

Принципы построения КО те же, что для СВ (18.3). Пусть задан уровень значимости a.

По таблице распределения Стьюдента по заданному уровню значи- мости a и числу степеней свободы п – 1 находим критические точки

136

(квантили) Tα ; n−1 распределения Стьюдента. По выборке (18.2) и формуле

2

(18.9) находим Тнабл.. Так как распределение Стьюдента симметрично от- носительно оси ординат (см. рис. 14.2), то при |Tнабл.| ³ Tα ; n−1 значения

2

критерия (18.9) попадают в КО и H0 отклоняется в пользу На. Если же |Tнабл.| < Tα ; n−1 , то Tнабл Î ОПГ и нет оснований отклонять H0.

2

18.5. Пример. По технической норме на выполнение операции О на конвейере часового завода отводится в среднем 40 с. От работниц по- ступили сигналы, что в действительности они затрачивают на операцию О больше времени. Произвели измерения времени на выполнение опера- ции О у 16 работниц. Оказалось, что среднее время на этой операции

Можно ли по имеющимся данным на уровне значимости a = 0,01 от- клонить гипотезу, что действительное среднее время исполнения опера- ции О соответствует технической норме?

О. Пусть H0: m = 40 с (техническая норма установлена верно), а На: m > 40 с (техническая норма установлена неверно, она занижена, нуж- но больше времени).

Известно, что СВ X (величина времени) на операции О подчиняет- ся нормальному закону распределения.

Ввиду На: m > 40 выбираем правостороннюю КО. Вычисляем

По таблице квантилей распределения Стьюдента по уровню значи-

мости a = 0,01 и числу степеней свободы n – 1 = 15 находим критическую правую точку T0,01;15 , удовлетворяющую условию Р(Т ³ T0,01;15 ) = 0,01. Это значение T0,01;15 = 2,602. Так как Tнабл. = 2,21 < 2,602, то нет оснований для отклонения нулевой гипотезы (т.е. для пересмотра технической нормы времени для исполнения операции О.) Ä.

Отметим без доказательства, что критерии (18.3) и (18.9) являются наилучшими в смысле теоремы 17.3.

137

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ

1. Элементы комбинаторики

Для решения задач с применением классического определения веро- ятности необходимо знание вопросов из элементарной алгебры, связанных с понятиями комбинаторики. Рассмотрим множество E, содержащее n эле- ментов:

E = {a1, a2,, a3,..., an}.

Сочетанием из n элементов по m элементов называется всякая часть множества E, содержащая m элементов, причем два различных сочетания отличаются друг от друга хотя бы одним элементом. Число сочетаний вы- числяется по формуле (лекция 1, (1.10):

Пусть, например, E = {a, b, c}. Подсчитаем число сочетаний по два элемента:

C32 = 3! = 3 . 2!

Выпишем эти сочетания: ab, ac, bc.

Размещением из n элементов по m элементов называется всякая упо- рядоченная часть множества E, содержащая m элементов. Два различных размещения отличаются друг от друга либо составом, либо порядком рас- положения элементов. Число размещений вычисляем по формуле (лекция

1, (1.8):

A32 = 3 × 2 = 6 .

Выпишем размещения из трех элементов по два элемента:

a b, b a, a c, c a, b c, c b.

138

Перестановкой из n элементов называется всякое упорядоченное множество, образованное из всех элементов множества Е:

Pn = n!

P3 = 3! =1× 2 ×3 = 6 .

Выпишем все перестановки: a b c, b c a, c a b, b a c, a c b, c b a.

Для комбинаторных задач справедлив принцип перечисления: если множество Е содержит n1 элементов 1-го типа, n2 – 2- го, …, nk – k -го типа, то число способов выбора m элементов из множества Е с условием, чтобы среди m выбранных элементов было m1 элементов 1-го типа, m2 – 2- го ти- па, …, m k – k-го типа будет равно:

причем m = m1 + m2 +…+ m k, n = n1 + n2 +…+ n k.

1.1. Пример. Комиссия состоит из председателя, его заместителя и еще пяти человек. Сколькими способами члены комиссии могут распреде- лить между собой обязанности?

О. В данном случае множество Е содержит 7 элементов (7 человек в комиссии). Из множества Е выбирается 2 элемента, 1-ый элемент среди этих 2-х – председатель, 2-ой – заместитель. Т.е. порядок расположения элементов – существенен, поэтому будем вычислять число размещений из 7-ми элементов по 2 элемента:

A72 = 7 × 6 = 42 .

Ответ: 42.

1.2. Пример. В бригаде рабочих пятеро имеют 1-ый разряд, 8 человек – 2- ой, 10 человек – 3- ий разряд. В командировку надо направить 6 рабочих, причем среди них должно быть по 2 человека, имеющих одина- ковый разряд. Сколько существует вариантов выбора командированных?

O. Множество Е содержит 5 + 8 + 10 = 23 элемента, причем n1 = 5 элементов 1-го типа, n2 = 8 – 2- го типа, n3 = 10 – 3- го типа. Выбираем m = 6 элементов таких, чтобы среди них было по m1 = m2 = m3 = 2 элемента каждого типа.

139

Используя принцип перечисления, получим:

Ответ: 12600.

1.3. Пример. Сколько трехзначных чисел, делящихся на пять, можно составить из цифр 0, 1, 2, 3, 4, 5, если каждое число не должно содержать одинаковых цифр?

O. Эти числа могут быть либо вида XY5 (последняя цифра – 5 , пер- вая X – не ноль, вторая Y – любая, кроме пятерки, т.к. одинаковых цифр число не содержит), либо вида XY0 (т.е. последняя цифра – ноль, первые две – любые, кроме нуля, т.к. он уже использован (цифры не повторяются).

Подсчитаем количество чисел 1-го вида: первую цифру можно вы- брать четырьмя способами (это может быть либо цифра 1, либо 2, либо 3, либо цифра 4), вторую – четырьмя способами (к оставшимся трем невы- бранным цифрам добавляется цифра «ноль») Итак, количество чисел 1-го вида будет равно:

l1 = 4 × 4 = 16.

Для чисел 2-го вида это количество будет равно: l2 = A52 = 5 × 4 = 20

(выбор первых двух цифр из цифр 1, 2, 3, 4, 5).

Итого: l = l1 + l2 = 16 + 20 = 36.

Ответ: из имеющихся цифр можно составить 36 чисел, делящихся на

5(цифры в числе не повторяются).

1.4.Пример. Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозмож- ные пятизначные числа, не содержащие одинаковых цифр. Определить ко- личество чисел, в которых есть цифры 2, 4 и 5 одновременно.

O. Цифра 2 может располагаться в любом месте пятизначного числа, т.е. существует 5 вариантов расположения цифры 2 в числе, тогда для цифры 4 осталось четыре варианта расположения, для цифры 5 – три вари- анта. Далее, из оставшихся цифр (1, 3, 6, 7, 8, 9) надо выбрать еще две

цифры, это можно сделать A62 = 6 ×5 = 30 вариантами. Окончательно:

l = 5 × 4 × 3 × 30 = 1800.

Ответ: можно составить 1800 чисел, отвечающих условию задачи.

140