Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Пальчик_Теория вероятностей

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2413 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

16.5. Теорема. |rXY| ≤ 1.

О. Пусть rXY = r. Ясно, что

(( y -

) - r ×

(x -

))2 ³ 0 .

(16.27)

Поэтому будет неотрицательной и сумма

1 n

(x - x))2

∑

(( y - y) - r ×

(16.28)

n i=1

Раскроем квадрат в (16.28) и разобьем на три суммы. Получаем

1 n

S 2

∑( y

- y)2 -

2r ×

∑( y - y)(x - x) + r2

∑(x

- x)2 ) =

SX2

n i=1

SX i=1

i=1

= (12.6), (16.19) = S 2 - 2r

XY +

SY2

× r2 = (16.22) =

SX2

= S 2 - 2r 2S 2 + r 2S

2 ³ 0 , или S 2 (1 - r2 ) ³ 0 . Откуда 1 ³ r2.

Ä.

16.6. Определение. Числа

= b = r

K XY

и r

X / Y

= b' = r

K XY

(16.29)

Y / X

SX2

SY2

называются коэффициентами линейной регрессии Y на X и X на Y соот-

ветственно.

Из (16.29) видно, что ρY / X

и ρX / Y

имеют одинаковые знаки. Если

они оба положительны (отрицательны), то Y и X одновременно возрастают (убывают).

Сила линейной связи между X и Y зависит от угла Q между прямыми (16.24) и (16.25). Чем меньше угол между ними, тем эта связь сильнее (см. рис.16.2). Из рисунка видно, что

121

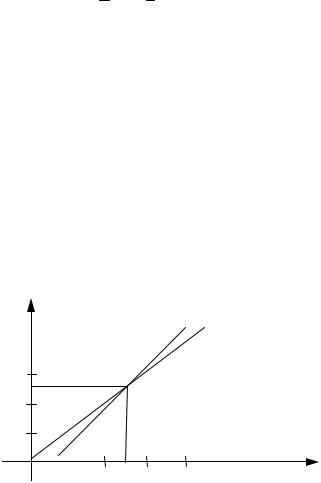
tgQ = tg( π - (a + b)) = ctg(a + b) =

1 − tgα tgβ

= (16.29) =

tga + tgb

1 - r 2

(16.30)

S 2

+ S

rXY

где tgα = b = ρ

, а tgb = b' = r

X / Y

. Пусть rXY = r.

Y / X

Если Q = 0°, то по (16.30) |r| = 1 и прямые (16.24) и (16.25) совпада-

ют, т.е. имеет место линейная функциональная зависимость между X и Y.

Если же 0 < Q < π , Q ® π , то линейная связь между X и Y уменьша-

ется и при Q = π из (16.30) следует, что rXY = 0 и тогда уравнения (16.24) и 2

(16.25) принимают вид y = y, x = x , откуда видно, что Y не зависит линей-

но от X, а X не зависит линейно от Y (но возможна нелинейная зависи- мость).

16.7. Пример. Найти уравнение регрессии Y на X и X на Y, а также коэффициент корреляции по четырем парам наблюдавшихся значений СВ

(X, Y):

(1; 2), (2; 4), (3; 5), (4; 7).

О.

Строим

поле

корреляции

на плоскости X0Y. Наносим точки

(xi , yi ),

i =

(рис. 16.3). Для удобства масштаб на оси 0Y выбран 1:1, а

1, 4

на оси 0X - 2:1.

∙ yx

∙

Рис. 16.3

122

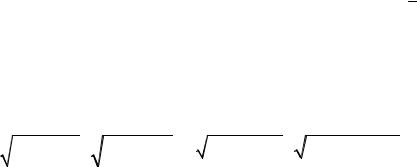
По характеру расположения точек делаем вывод, что нужно подби- рать уравнения регрессии линейного вида. Таблица вида (16.18) в нашем примере выглядит так:

Xi	yi	xi2	yi2	xi yi
1	2	1	4	2
2	4	4	16	8
3	5	9	25	15
4	7	16	49	28

10	18	30	94	53

По формулам (16.15) и (16.16) получаем a = 0,5; b = 1,6; a′ = – 0,269; b′ = 0,615. Уравнение регрессии Y на X по (16.12) имеет вид y X = 0,5 +1,6x.

Аналогично, уравнение регрессии X на Y имеет вид

Y = -0, 269 + 0,615 y.

По формуле (16.21) имеем:

13, 25 - 2,5 × 4,5

rXY =

= +0,99 »1.

- 6, 25 × 23,5 -

- (x)

( y)

7,5

20, 25

Связь между X и Y сильная. Это показывает и малый угол между прямыми регрессии на рис. 16.3. Ä.

17.Статистические гипотезы (основная терминология). Статистический критерий для проверки гипотез.

Наблюдаемые значения критерия. Критическая область (КО). Область принятия гипотезы (ОПГ). Критические точки.

Ошибки при принятии гипотез. Мощность критерия. Этапы проверки СГ

Пусть

x1, x2,…, x n –

(17.1 )

выборка объема n из ГС с неизвестной функцией распределения F(x).

123

Конечной целью исследования выборки (17.1) является получение выводов (решений) о свойствах всей ГС, например, о виде функции рас- пределения F(x, Θ1,…, Θn ) СВ X, которая образует рассматриваемую ГС, где Θ1,…, Θn – параметры функции распределения.

17.1. Определение. Статистической гипотезой (кратко: СГ) H назы- вается любое предположение относительно вида или параметров функции распределения (тогда H называют параметрической гипотезой) СВ X.

СГ с точно одним предположением называется простой гипотезой. Пусть дано m + 1 видов функций распределения:

P0, P1, …, P m .

(17.2)

Каждая из гипотез Hi: выборка (17.1) определяет ГС с функцией рас-

пределения Fi , i = 0, m , является простой гипотезой.

17.2. Определение. Одну из гипотез Hi , i = 0, m , выберем в качестве

основной. Ее называют нулевой гипотезой и обозначают H0. Остальные ги-

потезы Hi , i = 1, m , называют альтернативными.

После формулировки гипотез

H0, H1, …, H m

(17.3)

ставится задача их проверки с помощью выборки (17.1).

17.3.Определение. Процесс использования выборки (17.1) для про- верки истинности (ложности) СГ называется статистическим доказа-

тельством гипотезы.

17.4.Определение. Статистическим критерием (или просто кри-

терием) для проверки гипотез (17.3) называют СВ K, определенную на выборке (17.1), с помощью которой принимается решение о принятии или отклонении выдвинутой нулевой гипотезы. СВ K подбирают так, чтобы ее функция распределения была известна. (В качестве СВ K в МС использу- ются нормальная СВ, СВ Фишера, СВ Стьюдента и другие).

Формулировка гипотез (17.3) может принимать различный вид в зависимости от задачи исследования. Чаще всего формулируют основную гипотезу H0 и альтернативную Ha = H1.

17.5.Пример. Предположим, что по выборке (17.1) построена для СВ X нормальная модель распределения: N(m, σ). Тогда относительно параметров ГС X m и σ можно выдвинуть следующие гипотезы:

124

1. H0 : m = a0 Î R;				Ha : m ¹ a0, или m < a0 , или m >a0.
2. H0 : s = s0 Î R;				Ha : s ¹ s0, или s < s0, или s > s0.
3.	m = a				m ¹ a
3.	H0:	0 ;		Ha:		0 ,
	s = s0				s ¹ s0
где a0 и s0 –	конкретные действительные числа.
Итак, пусть для проверки некоторой СГ H0 подобрана подходящая
СВ K. Пусть известны f(K) и f(K/H0 ) –					плотность распределения СВ K при
условии, что H0 верна ((10. 9), (10.10)). Тогда из курса ТВ и МС известно,

что вероятность попадания значений СВ K в интервал K							α ; K α вычис-
						1−	2
							2	2
ляется по формуле
					K α
			α < K < K α ) =		2
		P(K	α < K < K α ) =		∫	f (K / H0 ) dK.		(17.4)
		1−	2	2	K
					1− α
					2
Обозначение границ выбранного интервала связано с тем, что обыч-
но вероятность попадания в интервал задают заранее числом 1 –								a, и тогда

границы интервала есть квантили K-распределения. На практике a = 0,05; 0,01; 0,001. Кроме того, при таком обозначении границ интервала предпо-

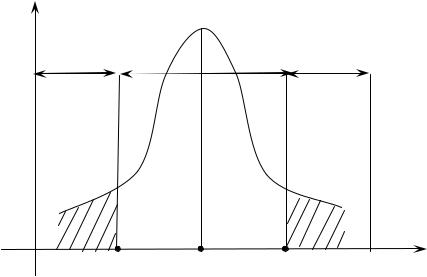
лагается, что кривая f(K/H0)		симметрична относительно моды K0 СВ K
(рис. 17.1).
f (К / H0 )

				KO
	KO		ОПГ
	KO

S = α	S = α
2	2

K	α	K0	K	α	K
1−	α	K0		α	K
	2			2
		Рис. 17.1

125

Для проверки гипотезы H0 по выборке (17.1) вычисляют частные значения входящих в критерий K величин и таким образом получают ча- стное значение критерия K, которое называют также наблюдаемым значе- нием K и обозначают Kнабл..

17.6. Пример. Предположим, что заданы две ГС, распределенные нормально. Нам нужно сравнить их дисперсии. Выдвигаем гипотезу

H0 : σ12 = σ22 .

Из теоремы 14.8 следует, что в качестве критерия K можно взять от- ношение исправленных выборочных дисперсий из двух выборок, сделан- ных для 1-й и 2-й ГС:


F =	S 2
	1	.	(17.5)

	2
	S 2

По теореме 14.8 F распределена по закону Фишера. По заданным двум выборкам могут быть найдены исправленные выборочные дисперсии

		2	2	= 5. Тогда
по формуле (12.17). Пусть, например, S1 = 20, S 2				= 5. Тогда
F	=	20	= 4.
F	=		= 4.
набл.	5
	5

После выбора K множество возможных значений СВ K разбивают на два непересекающихся подмножества: КО и ОПГ.

17.7.Определение. Критической областью (КО) критерия K назы-

вают совокупность значений критерия K, при которых основная гипотеза (H0) отвергается.

Областью принятия гипотезы (ОПГ) (H0) называется совокупность значений критерия K, при которых гипотеза H0 принимается.

17.8.Основной принцип проверки СГ. Если Kнабл. КО, то гипоте-

зу H0 отвергают. Если Kнабл. ОПГ, то гипотезу H0 принимают.

Точки, отделяющие КО и ОПГ, называются критическими и обозна- чаются как Kкр. (заметим, что обычно K есть НСВ и поэтому ее возможные значения заполняют сплошь некоторый интервал, поэтому КО и ОПГ – также некоторые интервалы, значит, существуют точки, которые эти ин- тервалы разделяют).

126

Различают правосторонние, левосторонние и двусторонние критиче- ские области.

Правосторонней называют КО, определяемую неравенством K > Kкр.

(рис. 17.2).

Ккр.

Рис. 17.2

Левосторонней называют КО, определяемую неравенством K < Kкр.,

т.е. K ] – ∞; Kкр.[ (рис. 17.3).

Ккр.

Рис. 17.3

Двусторонней называют КО, определяемую неравенствами: K < K1кр

и K > K2кр, K2кр > K1кр (см. рис. 17.1).

Как найти Kкр.?

Для этого нужно знать две вещи: число α (называемое уравнением значимости) и f(K/H0). Тогда из ТВ и МС известно, что

P(K >Kкр.) = ∫∞ f (K / H0 )dK = α	(17.6)
Kα

и квантиль K-распределения Kα и есть Kкр.. Аналогично,

P(K >K	кр.	) =	∫	K1−α f (K / H	0	)dK = α и K	= K	кр.	(17.7)
	кр.		∫		0	1−α		кр.

−∞

Ситуациям (17.6) и (17.7) соответствуют рис. 17.4 и 17.5.

127

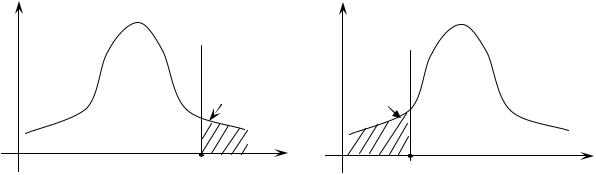
f (K / H0 )

ОПГ

S = α

S = 1− α

Kα K

Рис. 17.4

f (K / H0 )

ОПГ

S = α

S = 1− α

Kα

Рис. 17.5

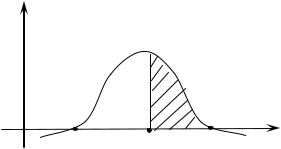
17.9. Замечание. Значок внизу при K (α при Kα и 1 – α при K1– α) означает площадь криволинейной трапеции, находящейся под кривой f(K/H0) и правее прямой K = Kкр., т.е. K = Kα или K = K1– α (см. 14.2).

В связи с замечанием 17.9 и определением 14.2 понятно и обозначение квантилей на рис. 17.1. В частности,

			P(K1кр.		< K <K2кр.) = 1 − α = ∫K2кр. f (K / H0 )dK ,
							K
							1кр.
где K	= K	α	, K	= K			, а f(K/H0) симметрична относительно моды K0 СВ K.
1кр.	1−	α	2кр.		α
		2				2

17.10.Замечание. Согласно принципу 17.8, если K КО, то H0 от- вергают, а если K ОПГ, то H0 принимают. Но в последнем случае это принятие H0 еще не означает, что H0 в самом деле верна. Просто K ОПГ нужно понимать в том смысле, что нет оснований отвергать H0.

17.11.Определение. В итоге принятия выдвинутой гипотезы H0 мо- гут быть допущены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута объектив- но верная гипотеза (H0).

Ошибка второго рода состоит в том, что будет принята объективно неправильная гипотеза (H0).

В таблице (17.8) даны возможные сочетания объективного состояния гипотезы H0 и субъективных действий на основании выборки (17.1).

Объективное	Субъективное статистическое решение

состояние	H0 принимается		H0 отвергается
гипотезы H0				(17.8)
Верна	Правильное решение		Ошибка 1-го рода

Неверна	Ошибка 2-го рода		Правильное решение

		128

17.12. Определение. Вероятность совершить ошибку 1-го рода на- зывают уровнем значимости и обозначают α.

Вероятность ошибки 2-го рода обозначают β, а вероятность 1 – β не- допущения ошибки 2-го рода (принятие H0 , когда она неверна) называют

мощностью критерия K.

Чем больше величина 1 – β , тем мощнее критерий K (при фиксиро- ванном уровне α сделать ошибку 1-го рода).

Дело в том, что ошибки 1-го и 2-го рода нельзя сделать одновремен- но как угодно маловероятными. Это наглядно видно на рис. 17.6.

f (K )

S = α

A B C K

Рис. 17.6

На рис. 17.6 AB – это ОПГ, BC – КО. Если K BC, то H0 отвергаем и возможна ошибка 1-го рода. Если K BA, то H0 принимаем и возможна ошибка 2-го рода. Если α уменьшить, то точка B сместится вправо. Но то- гда возрастет вероятность ошибки 2-го рода, так как AB увеличится.

Из этих рассуждений следует, что желательно задать вероятность ошибки 1-го рода заранее некоторым числом α, а среди критериев K вы- брать такой, который при данном уровне значимости α сводит к мини- муму вероятность ошибки 2-го рода.

17.13. Теорема Ю. Неймана – Э. Пирсона. Если α задано, то суще- ствует критерий K (среди всевозможных критериев), для которого мощ- ность 1 – β является максимальной. .

Исходя из вышеизложенного, статистическая проверка гипотезы со- стоит из следующих этапов:

17.14. Этапы проверки СГ.

17.14.1. Формулировка нулевой гипотезы H0 и альтернативной гипо- тезы H1.

17.14.2. Выбор критерия K для проверки гипотезы H0.

129

17.14.3.Выбор уровня значимости α.

17.14.4.Определение объема выборки n (если выборки нет).

17.14.5.Определение критической области и области принятия гипо-

тезы, т.е. нахождение критических точек.

17.14.6.Формулировка правила проверки гипотезы.

17.14.7.Принятие статистического решения.

17.15. Пример. Вероятность отказов лампочек подчиняется нор-

мальному распределению. Электроламповый завод гарантирует среднюю продолжительность безотказной работы лампочек в 800 часов со стан-

дартным отклонением в 120 ч. Выбрано 25 лампочек, произведенных за один день. В процессе их эксплуатации выяснилось, что их средняя про-

должительность работы равна 750 ч.

Можно ли утверждать, что лампы, произведенные в тот день, не удовлетворяют условиям гарантии?

О. Пусть m – средняя продолжительность горения лампочек в вы-

бранной партии из 25 ламп. По схеме 17.14 имеем:

1. Нулевая гипотеза H0: m = 800 ч; альтернативная гипотеза H1:

m< 800 ч.

2.В качестве СВ K (критерия проверки H0) выберем такую СВ, кото-

рая лучше всего характеризует ситуацию и для которой f(K) известна.

Пусть K N(0; 1). Такое распределение имеет стандартизированная СВ

(см. (18.12).

U= X − m .

σ/ 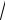n

Итак, пусть H0 верна. Тогда критерием может служить СВ

K = X − 800 = X − 800 .

120 / 25

3. Пусть α = 0,05. Тогда вероятность гарантированной продолжи-

тельности работы электрической лампы p= 1 – α = 0,95.

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2413 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб48умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб39умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб37умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб43умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб44умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб50умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб42умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб90умк_Яско_ Диф.уравнения_Ряды.pdf