
14-es_1 / Высшая математика (РТФ) / умк_Пальчик_Теория вероятностей
.pdf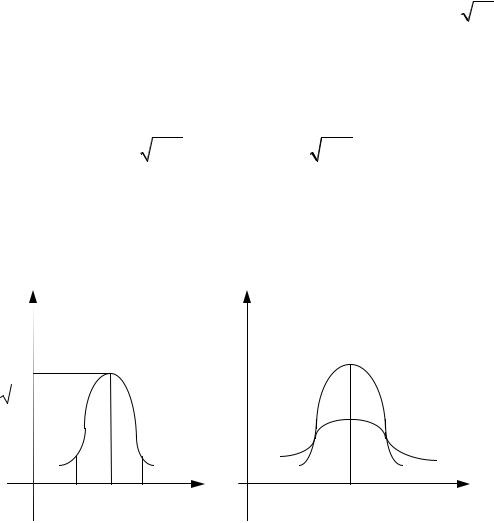
На практике правило «трех сигм» применяют следующим образом: предположим, что неизвестно распределение СВ X, но все наблюдаемые значения СВ X лежат в интервале ]m - 3σ; m + 3σ[, тогда есть основание полагать, что X распределена нормально.
График плотности распределения вероятностей, задаваемой форму-
лой (7.6), называют нормальной кривой, или кривой Гаусса.
Функция (7.6) может быть исследована с помощью дифференциаль- ного исчисления. При этом легко установить следующие ее свойства.
7.10. Свойства f(x).
7.10.1. Функция (7.6) имеет область определения (– ∞; + ∞). 7.10.2. f(x) > 0.
7.10.3. lim f (x) = 0 , т.е. асимптотой кривой Гаусса является ось Ox.
x→±∞
7.10.4. Кривая Гаусса имеет максимум в точке |
x = m, f (m) = |
1 |
|
. |
|
σ |
|
|
|||
2π |
|||||
Если σ увеличивается, то максимальная ордината уменьшается.
7.10.5.Кривая Гаусса симметрична относительно прямой x = m.
7.10.6.Кривая Гаусса имеет две точки перегиба с координатами
(m − σ, |
1 |
|
) |
и |
(m + σ, |
1 |
|
). |
||
σ |
|
|
σ |
|
|
|||||
2πe |
2πe |
|||||||||
7.10.7. Площадь фигуры, ограниченной кривой Гаусса, равна 1 (свойство любой плотности распределения f(x)) (рис. 7.1 и 7.2).
f (x) |
f (x) |
|||||
|
|
|
|
σ = |
1 |
|
|
|
|
|
|
||
1 |
|
|
2 |
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
2π |
|
|
|
|||
|
|
|
|
|
|
σ=1 |
|
|
|
x |
|
|
x |
|
|
|
m-σ m m+σ |
m=2 |
||
|
|
|
Рис. 7.1 |
Рис. 7.2 |
||
61
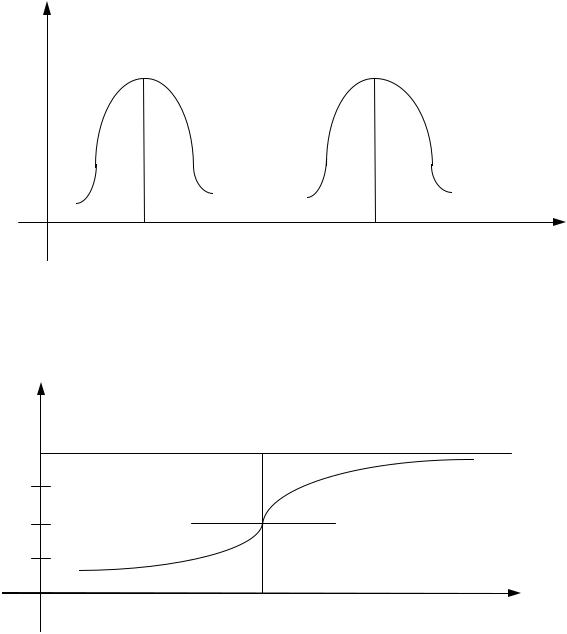
7.10.8. Если изменять m = M(X), то при σ = const кривая будет сме- щаться вдоль оси Ox (рис. 7.3.).
f (x)
x
m1 |
m2 |
Рис. 7.3
График функции Ф*(x) имеет вид, представленный на рис. 7.4.
Ф*(x)
1
0,75
0,5
0,25
x
0
Рис. 7.4
7.11. Замечание. Если X и Y – независимые СВ, распределенные нормально, то СВ X ± Y также распределена нормально.
В самом деле, из решения примера 6.2 следует, что СВ (Y) распреде- лена нормально (a = – 1 , b = 0). А из 4.2 в [3, с. 122 – 123] следует, что то- гда СВ X ± Y распределена нормально, причем МО
М(X ± Y) = M(X) ± M(Y), D(X ± Y) =D(X) + D(Y).
62
8. Понятие о законе больших чисел.
Понятие о центральной предельной теореме ТВ (ЦПТТВ)
Пусть E – опыт, в котором нас интересует признак X, или СВ X. При однократном проведении Е нельзя заранее сказать, какое значение примет X. Но при n-кратном повторении E «среднее» значение величины X (сред- нее арифметическое) теряет случайный характер и становится близким к некоторой константе.
Точно так же суммарное поведение значений n СВ X1, X2, ..., Xn ста- новится закономерным при соблюдении некоторых условий.
Знание этих условий позволяет поэтому прогнозировать «среднее» значение этих СВ X1, ..., Xn.
Изучение таких условий производится в ряде теорем ТВ, носящих
общее название закона больших чисел (ввиду n ®¥). |
|
|
|
|||||||||||||||||
8.1. |
(Неравенство Чебышева). Лемма. Пусть X – СВ, e > 0 – |
|||||||||||||||||||
любое число. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
P(| X | ³ e) < |
|
M ( X |
2 ) |
. |
|
|
|
|
(8.1) |
|||||||
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
O. Пусть f(x) – плотность вероятности для СВ X. Тогда |
||||||||||||||||||||
P(| X | ³ e) = ∫ |
f (x) dx = ∫ |
x2 |
× |
e2 |
f (x) dx £ |
∫ |
x |
2 |
f (x) dx = |
|||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|x|³e |
|
|
|x|³e e2 |
|
x2 |
|
|
|
|
|
|
|x|³e e2 |
|
|||||
|
1 |
|
|
1 |
¥ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
= |
∫ x2 f (x) dx £ |
∫ x2 f (x) dx = |
M ( X 2 ), |
|
|
|
||||||||||||||
e2 |
e2 |
|
e2 |
|
|
|
||||||||||||||
|
|x|³e |
|
-¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
так как e2 / x2 £ 1. Ä. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8.2. |
Следствие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
P(| X - M ( X ) | ³ e) £ |
D( X ) |
. |
|
|
|
(8.2) |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
||
O. Полагаем в |
(8.1) вместо |
|
X |
СВ X – |
M (X). Учитывая, что |
|||||||||||||||
M(X – M (X))2 = D(X), получаем (8.2). Ä. |
|
|
|
|
|
|
|
|
|
|
||||||||||
63

8.3. Следствие
P(| X - M ( X ) | < e) ³1 - |
D( X ) |
. |
(8.3) |
|
|||
|
e2 |
|
|
O. Это следует из (8.2) ввиду того, что события |X – M(X)| |
³ e и |
||
|X – M(X)| < e противоположны. Ä. |
|
||
8.4. Следствие (правило 3-х сигм для произвольного распреде- ления)
P(| X - M ( X ) |< 3sX ) ³1 - |
1 |
» 0,8889. |
(8.4) |
|
|||
9 |
|
|
|
O. Полагаем в (8.3) ε = 3σX и учитываем, что e2 = 9, s2X = 9D( X ). Ä. 8.5. Пример. Диаметр изготавливаемых деталей 10 мм. Разрешается допуск Dl = ± 0,1 мм. Какова вероятность, что взятая изготовленная деталь
бракована, если s2X = 0,0025 ?
О. Пусть Х – размеры детали. По условию М(Х) = 10 мм, e = 0,1,
D(X)= 0,0025. По (8.2) P(| X -10 |> 0,1) £ 0,0025 = 0,25. Ä. 0,01
8.6. Теорема Чебышева (закон больших чисел). Пусть
{X n}, n =1, ¥ - последовательность попарно независимых СВ, дисперсии которых ограничены одним и тем же числом C = const. Пусть каждая СВ Xi имеет МО M ( Xi ) = ai , i =1, n.Тогда для любого e > 0 имеет место
lim P(| |
X1 + K+ X n |
- |
a1 + K+ an |
|< e) =1. |
(8.5) |
|||
|
|
|||||||
n→∞ |
|
|
n |
|
n |
|
||
|
1 |
n |
|
|
|
|
|
|
O. Пусть Y = |
|
∑ X |
. Из свойств МО и дисперсии получаем, что |
|
||||
|
|
|||||||
n |
|
|
i |
|
|
|
|
|
|
n i =1 |
|
|
|
|
|
||
|
|
|
|
1 |
n |
|
|
|
M (Y ) = |
|
|
∑M ( X |
) = |
||||
|
|
|||||||
|
n |
|
|
n i=1 |
i |
|
||
|
|
|
|
|
|
|
||
|
1 |
|
n |
|
|
1 |
||
D(Y ) = |
|
|
∑D( X |
) £ |
|
|||
|
|
|
||||||
n |
|
n2 i=1 |
i |
|
n2 |
|||
|
|
|
|
|||||
Здесь мы воспользовались свойством, симых СВ равна сумме их дисперсий.
1 ∑n ai , n i =1
× n ×C = C . n
что дисперсия суммы незави-
64

Теперь из следствия 8.3 получаем, что
P(| Y - M (Y ) |< e) ³1 - |
D(Yn ) |
³1 - |
C |
. |
(8.6) |
|
|
|
|||||
n |
n |
e2 |
ne2 |
|
||
|
|
|
||||
|
Взяв предел при n ® ¥ от |
обеих частей (8.6), |
получаем, что |
||||
lim |
C |
= 0 и поэтому |
|
|
|
|
|
|
|
|
|
|
|
||
n→∞ ne2 |
|
X1 + K+ X n |
|
a1 + K+ an |
|
|
|
|
|
lim P(| |
- |
|< e) ³1. |
(8.7) |
||
|
|
|
|
||||
|
|
n→∞ |
n |
n |
|
||
Но вероятность не может быть больше 1. Поэтому в (8.7) знак нера- венства исключается. Поэтому (8.7) на самом деле есть (8.5). Ä.
8.7. Замечание. Обычно пользуются частным случаем теоремы
8.6, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
когда M ( Xi ) = a, D( Xi ) = s2 , |
"i = |
|
|
. Тогда (8.5) принимает вид |
|
|||||||||
1, n |
|
|||||||||||||
lim P(| |
X1 + K+ X n |
- a |< e) =1. |
|
(8.8) |
||||||||||
|
|
|
||||||||||||
n→∞ |
|
|
|
n |
|
|
|
|
||||||
Аналогично, (8.6) принимает вид |
|
|
|
|
|
|
|
|
|
|||||
P(| |
X |
1 |
+ K+ X |
n |
- a |< e) ³1 |
- |
s2 |
. |
(8.9) |
|||||
|
|
|
n |
|
|
ne2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8.8. Замечание. Теорему Чебышева 8.7 можно понимать и так: можно считать, что дана одна СВ X, которая измеряется (испытывается) n раз; случайное значение i-го испытания определяет СВ Xi. Тогда разность
между X1 + K+ X n и a (истинным значением X) мала при n ® ¥, то есть n
1 n
a » n i∑=1 Xi .
8.9. Теорема Бернулли. Пусть k – количество появлений события A в n испытаниях схемы Бернулли, причем вероятность наступления A в каждом испытании p = const. Тогда
lim P(| |
k |
- p |< e) =1, |
(8.10) |
|
|||
n→∞ |
n |
|
|
65

т.е.
|
|
|
|
|
|
k |
» p. |
|
|
(8.11) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
n |
|
|
|
|
|
О. Это следует из (8.8), так как ввиду (7.2²) M(Xi ) = p, а ввиду (7.3) |
|||||||||
X1 + K+ X n принимает значение k. Ä. |
|
|
|
|||||||
|
На (8.11) и основано статистическое определение вероятности. |
|||||||||
|
В законе больших чисел (теореме Чебышева и др.) указано лишь, что |
|||||||||
|
|
1 |
n |
|
|
|
|
1 n |
|
|
СВ Y = |
|
∑ X |
i |
принимает значения, близкие к значениям |
|
∑M ( X |
). |
|||
|
|
|||||||||
n |
|
n i=1 |
|
|
|
|
i |
|
||
|
|
|
|
|
|
n i=1 |
|
|||
Но в ТВ существует ряд теорем, в которых указываются условия, при которых закон распределения суммы большого числа СВ X1 + K+ X n близок к нормальному. Впервые одна из таких теорем была сформулирова- на и доказана русским математиком А.М. Ляпуновым (1857 – 1918). Эти теоремы называют центральными предельными теоремами ТВ.
8.10. (ЦПТТВ). Теорема. Пусть
{Xn} = {X1,…, X n, … }–
последовательность независимых и одинаково распределенных СВ с оди- наковыми математическими ожиданиями m = M(Xn ) и одинаковыми дисперсиями s2 = D(Xn ) "n. Тогда закон распределения СВ
|
|
X |
1 |
+K+ X |
n |
- n m |
|
|
1 |
|
n |
X |
k |
- m |
|
|||||||
Y = |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
∑ |
|
|
|
(8.12) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n |
|
|
|
s n |
|
|
|
|
|
|
|
|
n k =1 |
|
|
s |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
при n ® ¥ стремится к нормальному закону N(0,1), т.е. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
2 / 2dt = F (x). |
|
||||||||
lim |
P(Yn < x) = |
|
|
|
∫ ×e−t |
(8.13) |
||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||||
n→→∞ |
|
|
|
|
|
|
|
2p −∞ |
|
|
|
|
|
|
|
|
|
|
|
|||
Æ
8.10. ЦПТТВ (упрощенный вариант). Если СВ X есть сумма боль-
шого числа независимых СВ, влияние каждой из которых на всю сумму мало, то X имеет закон распределения, близкий к нормальному.
66
9. Понятие многомерной СВ. Распределение вероятностей многомерных дискретных СВ. Функция распределения непрерывной многомерной СВ. Плотность распределения непрерывной многомерной СВ
Пусть эксперимент Е имеет вероятностную модель (W, F, P). Если каждому элементарному событию w Î W ставится в соответствие n дейст- вительных чисел X1(w), ..., Xn(w), то говорят, что Е описывается n-мерной СВ (X1, ..., Xn).
9.1. Пример. Пусть Е состоит в изготовлении детали в форме па- раллелепипеда на станке. Тогда каждой изготовленной детали (w) можно поставить в соответствие следующие четыре признака: X1(w) – длина дета- ли, X2(w) – ширина детали, X3(w) – высота детали, X4(w) – вес детали. Та- ким образом, Е описывается 4-мерной СВ (X1, ..., X4 ), принимающей раз- личные возможные значения.
Составляющие (компоненты) X1,K, X n n-мерной СВ ( X1,K, X n ) яв- ляются одномерными СВ, рассматриваемыми совместно в некотором экс- перименте.
Пусть сначала n = 2.
По аналогии с функцией распределения одномерной СВ (F(x)=P(X<x)) можно определить функцию F(x, y), равную вероятности то- го, что в результате опыта компонента Х приняла значения, меньшие дей- ствительного числа х, и в то же время компонента Y приняла значения, меньшие y Î R:
F(x, y) = P(X < x, Y < y) = P(X < x Ç Y < y). |
(9.1) |
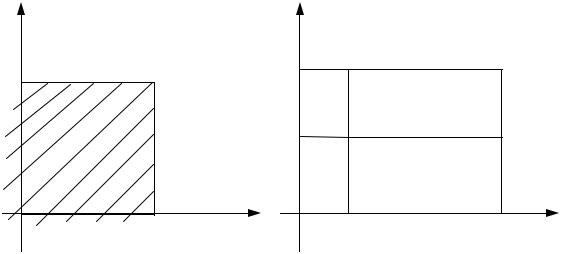
Из рис. 9.1. видно, что функция F(x, y) выражает вероятность попа- дания точки (х, у) в заштрихованную область (квадрант с вершиной (х, у)).
В частности, с помощью F(x, y) можно вычислить вероятность попа-
a £ X < b |
(рис. 9.2). |
|
дания значений СВ (X, Y) в прямоугольник |
|
|
c £ Y < d |
|
|
P(a £ X < b Ç c £ Y < d) = F(b, d) – F (b, c) – F (a, d) + F(a, c). |
(9.2) |
|
67
y |
y |
(a,d) |
(b,d) |
(x,y) |
|
(a,c) |
(b,c) |
x |
x |
Рис. 9.1 |
Рис. 9.2 |
Если компоненты X и Y в (X,Y) являются дискретными СВ, то и СВ (X,Y) называется дискретной. Для ДСВ (X, Y) закон распределения можно записать в виде таблицы (9.3)
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
x1 |
|
x2 |
|
... |
xi |
|
... |
xn |
|
|||
Y1 |
|
p11 |
|
p21 |
|
... |
Pil |
|
... |
Pn1 |
|
|||
Y2 |
|
p12 |
|
p22 |
|
... |
Pi2 |
|
... |
Pn2 |
(9.3) |
|||
M |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yj |
|
p1j |
|
p2j |
|
... |
Pij |
|
... |
Pnj |
|
|||
M |
|
M |
|
M |
|
M |
M |
|
|
M |
M |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ym |
|
p1m |
|
p2m |
|
... |
Pim |
|
... |
Pnm |
|
|||
В таблице (9.3) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
i = |
|
, |
|
|
||
|
|
pij |
= P( X = xi |
ÇY = y j ), |
1, n |
|
(9.4) |
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
j =1, m. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Зная таблицу (9.3), можно найти F(x) и F(y). Например,
( X = xi ) = {( X = xi ) Ç (Y = y1)} È{( X = xi ) Ç (Y = y2 )} ÈKÈ{( X = xi ) Ç (Y = ym )}.
Откуда по аксиоме ЗК имеем:
m |
|
|
P( X = xi ) = ∑ pij |
= Pi . |
(9.5) |
j =1
68
Аналогично
n |
|
|
P(Y = y j ) = ∑ pij |
= P j . |
(9.6) |
i=1
Если в (9.5) i пробегает значения от 1 до n, то получаем распределе-
ние компоненты Х. Его называют маргинальным распределением компо-
ненты Х. Аналогично получается и маргинальное распределение компо- ненты Y.
9.2. Определение. Функцией распределения непрерывной k-мерной СВ (Х1, ..., Хk ) называется вероятность появления события {X1 < x1 Ç X2 < x2 Ç … Ç Xk < xk }, рассматриваемая как функция переменных x1, ..., xk
F(x1, …, x k) = P{X1 < x1 Ç … Ç Xk < xk }. |
(9.7) |
9.3. Свойства F(x, y).
9.3.1. 0 £ F(x, y) £ 1 "(x, y) Î WXY. 9.3.2. x2 > x1 F(x2, y) ³ F(x1, y);
y2 > y1 F(x, y2 ) ³ F(x, y1 ),
т.е. F(x, y) является неубывающей по каждому аргументу (доказательство на основании рис. 9.1.).
9.3.3. |
F(x, y) непрерывна слева по каждому из аргументов. Æ. |
||
9.3.4. |
lim |
F (x, y) = 0, |
lim F (x, y) = 0 |
|
x→−∞ |
|
y→−∞ |
|
lim |
F (x, y) = 0, |
lim F (x, y) = 1. |
|
x→−∞ |
|
x→∞ |
|
y→−∞ |
|
y→∞ |
Доказательство. Докажем последнее равенство. В самом деле,
lim F (x, y) = P(x < ∞, y < ∞) = 100 % = 1.
x→∞ y→∞
9.3.5.При y = ¥ F(x, y) = F1(x) = FX(x). При x = ¥ F(x, y) = F2(y) = FY(y).
О. F(x, ¥)= P(X < x, Y < ¥)= P(X < x) = F1(x). Ä.
Любая функция со свойствами 9.3.1 – 9.3.5 является функцией рас- пределения некоторой СВ (X, Y).
69
Для дискретной СВ (X, Y) имеем
F (x, y) = ∑ P( X = xi ÇY = y j ), |
(9.8) |
xi < x y j < y
где суммирование производится по всем тем точкам (xi, yj ), для которых одновременно xi, < x и yj <y.
9.4. Определение. СВ (X, Y) называется абсолютно непрерывной, ес- ли ее функция распределения F(x, y) абсолютно непрерывна, т.е. сущест- вует некоторая функция f(x, y), называемая плотностью распределения вероятностей (X, Y) такая, что
x |
y |
|
F (x, y) = ∫ |
dx ∫ f (x, y) dy (x, y) R2. |
(9.9) |
−∞ |
−∞ |
|
Вероятностный смысл f(x, y)
Рассмотрим вероятность попадания значений СВ (X,Y) в прямо- угольник со сторонами x, y. По аксиоме ЗК
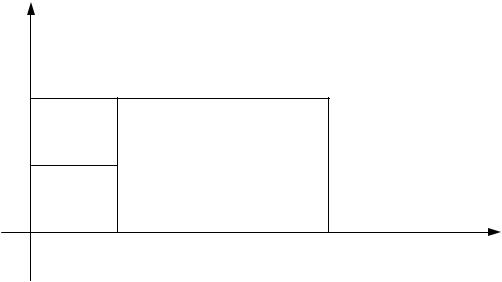
P(x £ X < x + D x Ç y £ Y < y + D y) = F (x + D x, y + D y) -
(9.10)
-F (x + D x, y) - F (x, y + D y) + F (x, y) (рис. 9.3.).
y
(x, y+ y) |
(x+ x, y+ y) |
y+ y
y |
(x, y) |
|
(x+ x, y) |
|
|||
|
|
|
x
x |
x+ x |
Рис. 9.3
70
