Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Пальчик_Теория вероятностей

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2420 21 22 23 24 > Следующая >>>

12. Числовые характеристики выборки: среднее выборочное, выборочная дисперсия,

выборочное среднее квадратичное отклонение,

выборочная мода, выборочная медиана

Средним значением выборки или выборочным средним называется

число

× ∑ xi

или

× ∑ m i xi ,

(12.1)

i =

i =1

где k – число неповторяющихся вариант.

Выборочной дисперсией называется число

D*(x) ≡ s в2 =

) 2

или D*(x) ≡ s в2

) 2 . (12.2)

× ∑ ( xi

× ∑ m i ( xi

i =1

Удобной для вычислений также является формула

D*(x) ≡ s в2

× ∑ m i xi2 -

2 ,

n = ∑mi .

(12.3)

i =1

i=1

Выборочным средним квадратичным отклонением называется число

σв =

D (x)

(12.4)

Выборочная медиана делит вариационный ряд на две равные части и вычисляется следующим образом: если n = 2m, то

Ме* =	xm + xm +1	, если n = 2m + 1, Ме* = xm+1,	(12.5)

2

где xm и xm+1 − элементы выборки. Выборочной модой называется элемент выборки, встречающийся с наибольшей частотой. Мода обозначается Мо*.

Смысл выборочных числовых характеристик рассмотрен в лек- ции 12.

191

12.1. Пример. Определить среднее, моду и медиану для выборки

7, 6, 9, 2, 3, 1, 1, 4.

О. Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4, 6, 7, 9.

Выборочное среднее x = 1 (1 + 1 + 2 + 3 + 4 + 6 + 7) = 4,125 по формуле (12.1). 8

Все элементы входят в выборку по одному разу, кроме 1, следовательно, Мо* = 1.

Так как m = 8, то медиана Ме* = 1 ·(3 + 4) = 3,5 согласно формуле (12.5). Ä 2

12.2. Пример. В условиях примера 11.2 найти среднее выборочное, выборочную дисперсию, выборочное среднее квадратичное отклонение.

О. Добавив в табл. 2 примера 11.2 середины интервалов

получим

X ,

табл. 1.

Таблица 1

– 0,14

– 0,12

– 0,10

– 0,08

– 0,06

– 0,04

– 0,02

– 0,12

– 0,10

– 0,08

– 0,06

– 0,04

– 0,02

– 0,00

∑mi

= 50

– 0,13

– 0,11

– 0,09

– 0,07

– 0,05

– 0,03

– 0,01

, k = 7

Выборочное среднее найдем по формуле

× ∑ xi

(n = ∑mi

);

i =1

= −

(4·0,13 + 8·,011 + 10·0,09 + 14·0,07 + 6·0,05 + 5·0,03 + 3·0,01) =

ˆ 2

= − 0,0752. Выборочная дисперсия равна D (x) =

- x

∑ m i × xi

i =1

= 1 (4·(– 0,13) 2 + 8·(– 0,11) 2 + 10·(– 0,09) 2 + 14·(– 0,07) 2 + 6·(– 0,05) 2 + 5·(– 0,03) 2 + 50

+ 3·(– 0,01) 2) − (– 0,0752) 2 = 0,0067 − 0,0057 = 0,001.

Выборочное среднее квадратичное отклонение равно σв = 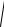D (x) = 0,0316. Ä

12.3. Пример. Произведено несколько измерений расстояния. Результаты измерений xi (i = 1,…15) в метрах представлены в виде

ряда (табл. 2).

192

Таблица 2

1235,6	1238,5	1234,5	1234,3	1236,2

1237,5	1234,2	1236,8	1237,5	1233,3

1232,9	1235,9	1237,6	1235,6	1233,3

Вычислить числовые характеристики выборки: x , D*(x) и σв.

О. Введем условные варианты ui = xi − a, где в качестве a возьмем число 1235, примерно среднее значение выборки. В результате получим таблицу условных вариант (табл. 3).

Таблица 3

0,6

3,5

– 0,5

– 0,7

1,2

2,5

– 0,8

1,8

2,5

– 1,7

– 2,1

0,9

2,6

0,4

– 1,9

Выборочное

среднее

этом случае вычисляется

по формуле

= a +

× ∑ ui = 1235 +

(0,6 + 3,5 + (– 0,5) + (– 0,7) + 1,2 + 2,5 + (– 0,8 ) +

i =1

+ 1,8 + 2,5 + (– 1,7) + (– 2,1) + 0,9 + 2,6 + 0,4 +

(– 1,9)) = 1235 +

(16 − 7,7) =

= 1235 + 0,55 = 1235,55.

Выборочная дисперсия вычисляется по формуле

D*(x) =

× ∑ u i2 - (

- a ) 2

((0,6)2 + (3,5)2 + (– 0,5) 2 + (– 0,7) 2 +

+(1,2)2 + (2,5)2 + (– 0,8) 2 + (1,8)2 + (2,5)2 + (– 1,7) 2 + (– 2,1) 2 + (0,9)2 +

+(2,6)2 + (0,4)2 + (– 1,9) 2) − (0,55) 2 = 3,321 − 0,3025 = 3,018.

Среднее квадратичное отклонение равно σв = 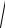D (x) = 1,737. Ä

12.4. Пример. Вычислить среднее значение и дисперсию группиро- ванной выборки (табл. 4), перейдя к условным вариантам по формуле:

	1	ˆ		Мо*
ui =		ˆ	−	Мо*	),
ui =		( xi	−		),
	h

где h − длина интервала.

193

								Таблица 4
	X	144 − 148	148	− 152	152 − 156	156 − 160	160 − 164	164 − 168

	mi	1		3	15	18	14	2
		О. Длина интервала h = 4, объем выборки n = ∑mi = 53, значение
середины интервала,				встречающееся		с наибольшей частотой, – мода

Мо* = 158. Таким образом, преобразование последовательности середин интервалов выполняется по формуле

				1	ˆ
			ui =		ˆ	− 158), i = 1,2,...6.
			ui =		( xi	− 158), i = 1,2,...6.
				h
	Результаты расчетов приведены в табл. 5.
									Таблица 5

		xi	ui				mi	ui mi	ui2 mi2
1		146	– 3				1	– 3	9

2		150	– 2				3	– 6	12

3		154	– 1				15	– 15	15

4		158	0				18	0	0

5		162	1				14	14	14

6		166	2				2	4	8

∑							53	– 6	58

Вычисляем среднее и выборочную дисперсию по формулам:

+ Мо* =

× ∑ui × mi

·(−6) + 158 = 157,546.

i=1

D*(x) = (

× ∑uimi -

× (∑uimi )2 ) × h2 =

−

·(−6)

2)·42 = 17,728. Ä

532

194

Задачи для самостоятельного решения

1.Вычислить среднее, дисперсию, моду и медиану следующих вы-

борок: а) 1, 2, 3, 4, 5, 5, 9; б) 1, 2, 3, 4, 5, 5, 12.

Сравнить полученные числовые результаты для выборок а) и б).

2.Определить x , Мо*, Ме*, D*(x) группированной выборки:

X	5 – 7	7 – 9	9 – 11	11 – 13	13 – 15	15 – 17

m	8	14	40	26	6	4

3. Для приведенной ниже выборки выполнить следующие задания:

1)вычислить среднее и дисперсию негруппированной выборки, вве- дя условные варианты по формуле: ui = xi − a;

2)вычислить среднее и дисперсию, предварительно проведя группи- ровку выборки с заданной длиной интервала h = 2 и преобразовав данные по формуле:

	1	ˆ		*
ui =		ˆ	−	Мо	).
ui =		( xi	−	Мо	).
	h

Положительные отклонения размера от номинала у партии деталей

(в мм):

17	21	8	20	23	18	22	20	17	12
20	11	9	19	20	9	19	17	21	13
17	22	22	10	20	20	15	19	20	20
13	21	21	9	14	11	19	18	23	19.

4. На телефонной станции производились наблюдения за числом не- правильных соединений в минуту. Наблюдения в течение часа дали сле- дующие результаты:

3,	1,	3,	4,	2,	1,	1,	3,	2,	7,	2,	0,	1,	2,	1,
2,	4,	0,	3,	0,	2,	0,	1,	3,	3,	1,	2,	0,	3,	4,
2,	0,	2,	1,	4,	3,	4,	2,	0,	2,	3,	1,	1,	2,	2,
3,	1,	4,	2,	2,	1,	2,	5,	1,	1,	0,	1,	1,	1,	5.

Записать вариационный статистический ряд, оценить среднее и дис- персию числа неправильных соединений.

195

13. Точечные оценки параметров распределения. Несмещенность, состоятельность и эффективность.

Метод максимального правдоподобия

Статистической оценкой неизвестного параметра генеральной со- вокупности называется функция от наблюдавшихся случайных значений этого параметра, образующих выборку. Статистические оценки делятся на точечные и интервальные. Статистическая оценка, определяемая одним числом, называется точечной.

Качество оценок характеризуется следующими свойствами:

1. Н е с м е щ е н н о с т ь. Оценка θ * называется несмещенной

оценкой параметра θ , если М( θ ) = θ . Разность М( θ ) −					θ называется сме-
щением.
2.	С о с т о я т е л ь н о с т ь.	Оценка θ = θ n называется состоя-
тельной	оценкой параметра θ , если	lim P(	θ − θ	<	ε) = 1 или если
тельной	оценкой параметра θ , если	lim P(	θ − θ	<	ε) = 1 или если
		n→∞
M( θ n) → θ и D( θ n) → 0 при n → ∞.
3.	Э ф ф е к т и в н о с т ь. Оценка θ * называется эффективной, ес-

ли при заданном объеме выборки она имеет наименьшую возможную дисперсию.

Оценка математического ожидания M(x) генеральной совокупности – выборочная средняя x является несмещенной, состоятельной и эффективной.

Оценка генеральной дисперсии D(x), вычисленная по формуле

2 n *

S = n − 1 ·D (x), (13.1)

называется исправленной выборочной дисперсией. Оценка S2 является не- смещенной, а оценка D*(x) − состоятельной для генеральной дисперсии D(x).

Свойства точечных оценок рассмотрены в лекции 12.

Для нахождения точечных оценок неизвестных параметров распре- деления используются различные методы, в частности, метод максималь-

ного правдоподобия.

Функцией правдоподобия случайной величины Х называется функция аргумента θ :

а) для дискретной СВ

L(x1, x2, …, xn; θ ) = P(x1, θ )·P(x2, θ )·… P(xn, θ ),

(13.2)

196

б) для непрерывной СВ

L(x1,	x2, …,	xn; θ ) = f(x1, θ )·f(x2, θ )·… f(xn, θ ),	(13.3)
где x1, x2, …,	xn −	элементы выборки.

В качестве точечной оценки параметра θ принимают θ *, при кото- ром функция правдоподобия достигает максимума.

На практике удобнее пользоваться функцией ln L, максимум которой находится следующим образом:

1) найти производную d ln L ; dθ

2) приравнять производную к нулю и найти критическую точку;

3) найти вторую производную	d 2 ln L	; если вторая производная при
	dθ2

θ = θ * отрицательна, то θ * − точка максимума.

Найденную точку максимума θ * принимают в качестве оценки мак- симального правдоподобия (МП-оценки) параметра θ .

Замечание. Метод максимального правдоподобия можно применять,

когда θ = ( θ 1, , θ m) − многомерный параметр. Функция максимального правдоподобия будет достигать максимума в той точке θ , в которой все частные производные по θ k , k = 1, 2,…, m, равны нулю.

Основные методы нахождения точечных оценок рассмотрены в лекции 13.

13.1. Пример. Для определения точности измерительного прибора, систематическая ошибка которого равна нулю, было произведено 5 неза- висимых измерений, результаты которых представлены в табл. 1.

					Таблица 1
Номер	1	2	3	4	5
измерения	1	2	3	4	5
измерения

xi	3781	3836	3807	3763	3858

Определить несмещенную оценку дисперсии ошибок измерительно- го прибора, если значение измеряемой величины M(x)

а) известно и равно 3800 м; б) неизвестно.

197

О. а) так как M(x) = 3800, то несмещенная оценка дисперсии опреде- ляется по формуле

S2 =

- M (x))2

6439

= 1609,75 м2;

× ∑(x

n -1

i =1

б) значение измеряемой величины неизвестно, поэтому ее оценка

∑xi = 3809 и несмещенная оценка дисперсии равна

n i=1

S2 =

)2 =

6034

= 1508,5 м2.

× ∑(xi -

Ä.

n -1 i =1

13.2. Пример. Пусть x1 = 64, x2 = 56, x3 = 69 − число автолюбителей, заправившихся на данной станции с 8-ми до 11-ти часов утра соответст- венно в 1-й, 2-ой и 3-й дни. Предположим, что число автолюбителей, подъезжающих на заправку, есть случайная величина X, имеющая распре- деление Пуассона с параметром q = 3λ, где λ − ожидаемое число заправ- ляющихся автолюбителей в течение одного часа. Найти МП-оценку пара- метра λ. Показать, что полученная оценка является несмещенной, состоя- тельной и эффективной.

О. Для распределения Пуассона P(x, q ) = qx

·e−θ , и функция прав-

доподобия L(x1, x2, x3; q ) = P(x1, q )·P(x2, q )·P(x3, q ) =

= qx1

e−θ · qx2

e−θ · qx3

e−θ = e−3θ · q64+56 + 69

= e−3θ ·

q189

x1!

x2!

x3!

64!×56!×69!

Логарифмическая функция правдоподобия равна

ln L = − 3 q + 189·ln q − ln(64!56!69!).

Находим производную

d ln L

и приравниваем ее к нулю:

d ln L

= − 3 +

189

= 0;

3 q = 189;

q = 63.

Так как q = 3λ, то λ = 21.

При этом 21 =

·(64 + 56 + 69) =

(среднее число заправляю-

щихся автолюбителей в течение одного часа). Таким образом, МП-оценка параметра λ равна x , следовательно, она является несмещенной, состоя- тельной и эффективной. Ä.

198

13.3. Пример. По выборке x1 = 5,10; x2 = 5,15; x3 = 5,15; x4 = 5,20

объема n = 4 найти МП-оценку неизвестного параметра θ нормального распределения N(a,1) ( θ = a; σ = 1). Показать, что полученная оценка яв-

ляется несмещенной и состоятельной.

О. Так как для нормального распределения N(a, 1)

−

( x−a)2

f( x, a, 1) =

, то функция правдоподобия равна

2π

L(x1, x2, x3, x4, a, 1) = f(x1, a, 1)·f(x2, a, 1)·f(x3, a, 1)·f( x4, a, 1) =

−

( x −a)2

−

( x −a)2

−

( x −a)2

−

( x −a)2

2π ×

−

( x −a)2

+( x −a)2 +( x −a)2 +( x −a)2

× e

( 2π )4

−

(5,10−a)2 +2(5,15−a)2 +(5,20−a)2

·e

4π 2

Логарифмическая функция правдоподобия равна

ln L = – ln(2π)2 −

[(5,10− a)2 + 2(5,15− a)2 + (5,20− a)2], отсюда

d ln L

[2(5,10− a) + 4(5,15− a) + 2(5,20− a)] = 0;

5,10 −

a + 10,30 − 2 a + 5,20 − a = 0;

4a = 20,60;

a = 5,15.

Таким образом, МП-оценка неизвестного параметра a равна 5,15.

Но 5,15 = 1 (5,10 + 5,15 + 5,15 + 5,20) = x . 4

Следовательно, эта оценка является несмещенной и состоятельной. Ä.

199

13.4. Пример. Методом максимального правдоподобия найти оценки

				−	( x−a)2
	1		× e		2σ	2

параметров						,
	s
		2p

если в результате n испытаний величина X приняла значения x1, x2,..., xn.

О. Составим функцию правдоподобия, учитывая, что θ 1 = a, θ 2 = σ:

L =	1			e	− (∑ ( xi − a)	2 / 2σ 2 )	.
	σ n (		)n
		2π

Найдем логарифмическую функцию правдоподобия:

−

∑(x

− a)2

ln L = − n ln σ + ln

(

2σ2

2π

Найдем частные производные по a и по σ:

∂ ln L ∑x

− na

∂ ln L

n ∑(x − a)2

∂a

;

∂σ

= −

σ2

σ3

Приравняв частные производные к нулю и решив полученную сис- тему двух уравнений относительно a и σ2, получим:

a = ∑ xi / n = x ; σ2 = (∑(xi − x )2) / n = Dв .

Таким образом, a* = x , σ* = 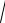Dв .

Найдем частные производные второго порядка и убедимся в том, что

∂ 2 ln L

= −

они отрицательны при a = a* и σ = σ*:

∂a2

< 0 для любого

σ2

∂ 2 ln L

3∑x

− a)2

nσ2 − 3∑(x − a)2

значения параметра a;

∂σ2

−

;

σ2

σ4

∂ 2 ln L

∑(xi -

)

2 - 3∑(xi

)

при a = x и σ

= (∑(xi −

) / n

x )

∂σ2

(∑(xi

)2 )2 / n2

- 2n2

< 0. Отсюда следует, что при a

= x ,

= D

функция

∑(x -

200

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2420 21 22 23 24 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб48умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб39умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб37умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб43умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб44умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб50умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб42умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб90умк_Яско_ Диф.уравнения_Ряды.pdf

17	21	8	20	23	18	22	20	17	12
20	11	9	19	20	9	19	17	21	13
17	22	22	10	20	20	15	19	20	20
13	21	21	9	14	11	19	18	23	19.

3,	1,	3,	4,	2,	1,	1,	3,	2,	7,	2,	0,	1,	2,	1,
2,	4,	0,	3,	0,	2,	0,	1,	3,	3,	1,	2,	0,	3,	4,
2,	0,	2,	1,	4,	3,	4,	2,	0,	2,	3,	1,	1,	2,	2,
3,	1,	4,	2,	2,	1,	2,	5,	1,	1,	0,	1,	1,	1,	5.

17	21	8	20	23	18	22	20	17	12
20	11	9	19	20	9	19	17	21	13
17	22	22	10	20	20	15	19	20	20
13	21	21	9	14	11	19	18	23	19.

3,	1,	3,	4,	2,	1,	1,	3,	2,	7,	2,	0,	1,	2,	1,
2,	4,	0,	3,	0,	2,	0,	1,	3,	3,	1,	2,	0,	3,	4,
2,	0,	2,	1,	4,	3,	4,	2,	0,	2,	3,	1,	1,	2,	2,
3,	1,	4,	2,	2,	1,	2,	5,	1,	1,	0,	1,	1,	1,	5.

17	21	8	20	23	18	22	20	17	12
20	11	9	19	20	9	19	17	21	13
17	22	22	10	20	20	15	19	20	20
13	21	21	9	14	11	19	18	23	19.

3,	1,	3,	4,	2,	1,	1,	3,	2,	7,	2,	0,	1,	2,	1,
2,	4,	0,	3,	0,	2,	0,	1,	3,	3,	1,	2,	0,	3,	4,
2,	0,	2,	1,	4,	3,	4,	2,	0,	2,	3,	1,	1,	2,	2,
3,	1,	4,	2,	2,	1,	2,	5,	1,	1,	0,	1,	1,	1,	5.