Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Пальчик_Теория вероятностей

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 244 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Свойства f(x)

4.12. f(x) ³ 0 (следует из 4.8(3°).

4.13.

∞
∫ f (x) dx =1.	(4.10)
−∞
О. Ввиду (4.9) несобственный интеграл	∞
О. Ввиду (4.9) несобственный интеграл	∫ f (x) dx выражает вероят-
	−∞
ность попадания значений СВ Х в интервал (–	¥, + ¥), что, конечно, равно

100 % = 1. Ä.

4.14. Теорема. Вероятность попадания значений СВ Х в интервал ]a, b[ вычисляется формулой

	β
P(a < X < b) = ∫ f (x) dx .		(4.11)
	α
О. Из (4.5) и (4.6) получаем: P(a < X < b) = F(b) – F (a) = (по форму-
β	β
ле Лейбница – Ньютона) = ∫ F '(x )dx =∫ f (x )dx . Ä .
α	α
4.15. Следствие.
x
F (x) = ∫	f (t) dt.	(4.12)

−∞

Таким образом, тройки (WX, FX, F(x)) и (WX, FX, f(x)) являются экви- валентными моделями эксперимента Е, описываемого СВ Х. Эти модели также иногда называются законами распределения СВ Х.

4.16. Пример. СВ Х задана плотностью распределения вероятностей

f (x) =			1- \| x \|, " \| x \| £1
			0, " \| x \| >1.
Найти F(x) и P( X >	1	).
Найти F(x) и P( X >		).
2

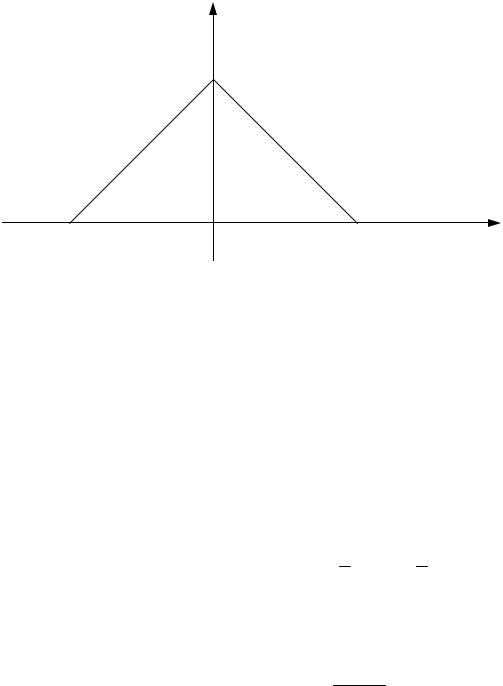
О. Разобьем интервал ]– ¥, + ¥[ на 4 интервала: ] – ¥, – 1] È ]– 1, 0] È ]0, 1] È]1, + ¥[. Тогда график f(x) на каждом из этих интервалов имеет вид, изображенный на рис. 4.2.

f (x)

-1	0	1
	Рис. 4.2
Далее по 4.15:
	x
	F (x) = ∫ f (t) dt.
	−∞
	x
Поэтому для "x £ – 1	имеем: ∫ 0 × dt = 0.

−∞

Для "x Î ]– 1, 0]		имеем:
−1	x		(1 + t)2	x		1 + 2x + x2
∫	0 × dt + ∫ (1 + t)dt =			\|−1	=
∫	0 × dt + ∫ (1 + t)dt =		2	\|−1	=	2
−∞	−1		2			2
−∞	−1

Для "x Î ]0, 1] имеем:

−1			0				x				(1 + t)2
∫ 0 × dt + ∫					(1 + t) dt + ∫(1 - t) dt = 0 +
											2
−∞				−1		0

=	1	+	-	1 - 2x + x2		+	1	= -	1	x2 + x +		1	.

	2				2	2		2			2

- 0 = 1 x2 + x + 1 . 2 2

|0−1 - (1 - t)2 |x0 = 2

Для "x Î ]1, +¥[ имеем:

−1 0 1 x

∫ 0 × dt + ∫ (1 + t) dt + ∫(1 - t) dt + ∫0 × dt =

−∞					−1			0				1
	1			1 - 2t + t 2			1		1				1
=		+	-			\|	0	= -		-	0	-		=1.
=		+	-			\|		= -		-	0	-		=1.
	2			2					2
	2			2					2				2

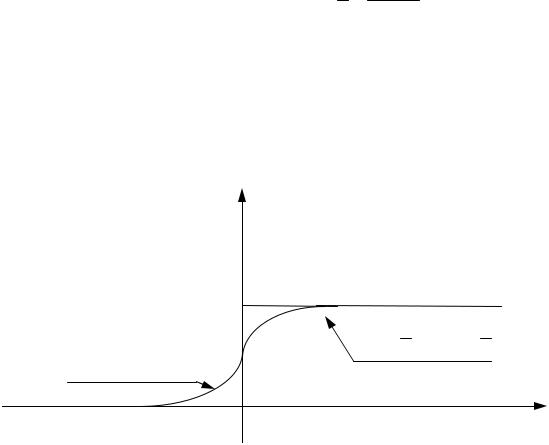
График F(x) изображен на рис. 4.3.

F(x)

				1
y =	1	x2 + x +	1		1
y =		x2 + x +			1
2		2		2
				2
		∙				∙
		-1		1

Рис. 4.3

1+ (1 - t)2 |10 =

y = - 1 x2 + x + 1 2 2

Далее, по 4.13:

		1						1							∞										1						∞
P( X >		1	) = P(					1	< X < ¥) = ∫ f (t) dt = ∫(1 - t) dt + ∫ 0 × dt =
P( X >			) = P(						< X < ¥) = ∫ f (t) dt = ∫(1 - t) dt + ∫ 0 × dt =
2							2									1										1					1
																1										1					1
														2											2
= -	(1 - t)2			\| 11			+ 0 = 0 - (-					1		)2 / 2 =						1	.
= -				\| 11			+ 0 = 0 - (-							)2 / 2 =							.
2												2					8
2												2					8
2
Другим способом, по 4.9: P( X >																						1		) = P(				1	< X < ¥) = P(					1	< X <1) =
Другим способом, по 4.9: P( X >																								) = P(				2	< X < ¥) = P(					2	< X <1) =
																	2											2						2
= F (1) - F (					1	) = -				1	+1 +		1		-		-	1	+				1		+		1	=1 +		1	-1 =	1	.	Ä
= F (1) - F (						) = -					+1 +				-		-		+						+			=1 +			-1 =		.	Ä
2							2					2					8 2										2	8			8

5. Схема испытаний Бернулли. Биномиальный закон распределения дискретной СВ.

Наивероятнейшее число появлений события. Предельные случаи в схеме Бернулли:

закон распределения Пуассона; локальная теорема Муавра-Лапласа; интегральная теорема Муавра-Лапласа. Равномерное и показательное распределения

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна p. Требуется вычис- лить вероятность

Рn (k)

того, что при этих n испытаниях событие A появится точно k раз.
5.1.	Теорема Бернулли.
	P (k) = C k × pk × (1 - p)n−k .		(5.1)
	n	n
О.	Пусть вероятность ненаступления A в единичном опыте равна

q = 1 – p. Вероятность сложного события B «в n опытах A наступит k раз и

не наступит n – k										раз» вычислим по теореме умножения независимых со-
бытий. P(B) = pk qn-k. Таких сложных событий B может быть Cnk																																			штук. (На-
пример, если n = 4, k = 3, то для B имеются следующие возможности:
						A, A					AA,												3 ). Эти сложные события (вида B) не-
AAA	A	, AA		A		A, A			A		AA,						A AAA. Их C						3 ). Эти сложные события (вида B) не-
																							4
совместимы. Поэтому число P(B) нужно сложить Cnk раз.																															Ä.
	5.2. Пример. Два равносильных шахматиста играют. Что вероят-
нее, выиграть 2 партии из 4-х, или 1 из 2-х?
	О. P (2) = C 2											× (		1		)2 (			1		)2 ;	P (1) = С1		×	1	×	1	;	P (2) =	4 ×3		×	1	×	1	=		6	;
	О. P (2) = C 2											× (				)2 (					)2 ;	P (1) = С1		×		×		;	P (2) =			×	4	×	4	=	16		;
	4									4		2					2					2	2	2		2			4		2		4		4		16
P (1) = 2 ×			1	×	1		=	1		;			1		>			3		. Ä.
P (1) = 2 ×				×			=			;					>					. Ä.
2	2			2			2					2					8
	2			2			2					2					8

5.3.Биномиальный закон распределения дискретной ДСВ

	X	0	1	...	k	...	n

	P(X = k)	Pn(0)	Pn(1)		Pn(k)	...	Pn(n)	(5.2)
	О. Если произвели n опытов, то A может появиться 0 раз, 1 раз, 2,...,
k раз, ... , n раз. Если СВ X –			появление A k раз в n опытах (P(A) = const = p), то

(5.2) и дает нам закон распределения СВ X. То, что во второй строке таб- лицы (5.2) сумма чисел равна 1, следует из того, что p + q = 1, и из форму- лы бинома Ньютона и из (5.1):

(q + p)n = qn + Cn1 pqn−1 +K + Cnk pk qn−k +K + pn

(поэтому и закон назвали биномиальным). Ä.

Закон (5.2) позволяет также вычислять возможность того, что A поя- вится от k до l раз, где

0 £ k < l £ n.

В самом деле, в силу несовместимости событий в схеме Бернулли

Pn(k ≤ m ≤ l) = Pn(k) + Pn(k + 1)+ …+ P n(l).

(5.3)

5.4. Пример. По каналу связи передается 5 сообщений. Каждое со- общение независимо от остальных искажается помехами с вероятностью 0,3. Найти вероятности событий: а) не более 2-х сообщений искажены; б) все сообщения без искажений; в) не менее 2-х сообщений искажены.

О.

а) P5 (0 £ m £ 2) = 0,30 × 0,75 + C51 × 0,3 × 0,74 + C52 × 0,32 × 0,73 » 0,84;

б) q =1 - p = 0,7; P5 (5) = C55 × 0,75 = 0,168;

в) P5 (2 £ m £ 5) = C52 × 0,32 × 0,73 + C53 × 0,33 × 0,72 + C54 × 0,34 × 0,71 +

+C55 × 0,35 = 0,3143. Ä.

Функция Pn(k) из (5.1) при некотором k0 достигает наибольшего зна- чения. Тогда число k0 называют наиболее вероятным числом появления события A при n испытаниях.

Заметим, что

Pn (k + 1)

= (5.1) =

n − k

(5.4)

P (k )

k +1

Откуда P (k +1) > P (k ) Û

n − k

>1~k < n p-q,

k +1 q

а P (k +1) < P (k) Û

n − k

<1~k > n p-q.

k +1

Итак, при k < np - q функция Pn (k) возрастает, а при k > np - q эта функция убывает. Но тогда существует точка k0 , в которой Pn (k) достигает максимума. То есть Pn (k0 ) больше значений Pn (k) в соседних точках. В ча- стности,

Pn (k0 ) ³ Pn (k0 -1)	(5.5)
Pn (k0 ) ³ Pn (k0 +1)

Применяя формулу (5.1) и решая неравенства (5.5) (относительно k0), получим

np – q £ k0 £ np + p.

(5.6)

5.5. Пример. Завод допускает брак в 1/45 своей продукции. Изго- товлено 4500 единиц продукции. Найти наиболее вероятное число единиц продукции, удовлетворяющее стандарту.

О. q = 1 , для стандарта p =1 - q = 44 .

45					45
По (5.6) 4500 ×	44	-	1	£ k0	£ 4500 ×	44	+	44	. Откуда k0 @ 4400. Ä.

45		45			45		45

Формулой (5.1) пользоваться неудобно при больших n. Существует ряд приближенных более простых формул для случаев, когда n ® ¥.

5.6. Теорема (Пуассона). Пусть вероятность события A при каж- дом из n независимых испытаний равна l /n, где l = const, l > 0. Тогда

lim P (k ) = lk				e−λ	;	(5.7)
n→∞	n	k !
n→∞		k !
P (k ) » lk			e−λ .			(5.7¢)
n		k !
		k !

О.

lim P (k ) = (5.1) = lim

pk (1 - p)n−k =

n→∞

k !(n - k )!

= lim

(l)k (1 - l)n−k = lk

× lim (

n(n -1)K(n - k +1)

× (1 - l)n−k ) =

k !(n - k )! n

k ! n→∞

= lk

× lim (1× (1 -

)(1 -

)K(1 -

k -1

)(1 - l)n (1 - l)−k ) =

k !

→∞

= lk

×1× lim (1 - l)n ×1 = lk

× e−λ .

Ä.

k !

n→∞

k !

Формулы (5.7) называются формулами Пуассона, или законом рас-

пределения редких ( p = λ ® 0!) явлений.

Заметим, что

∞

= e

(5.8)

∑

k !

k =0

Поэтому

∞

−λ

= e

−λ

∞

= (5.8) = e

−λ

=1.

(5.9)

∑

= e

∑

k =0

k !

k =0

k !

Рассмотрим дискретную ДСВ – число появлений события A в n неза- висимых испытаний, которая принимает значение k с вероятностью (5.7).

Говорят, что X распределена по закону Пуассона (5.10)

X	0	1		...	k		...
P(X=k)	e−λ	λ	−λ	...	lk	−λ	...	(5.10)
		e			e
		1!			k !

Ввиду (5.9) сумма чисел во второй строке таблицы (5.10) равна 1. Поэтому закон (5.10) является полным (корректным) ввиду (4.4).

Функция распределения закона (5.10) имеет вид:

F (x) = P( X < x) = ∑	lxi	e−λ .	(5.11)
x < x	xi !
i

Формула (5.7') является удобной математической моделью простей- шего потока событий. К СВ, подчиненным закону (5.7'), приводят практи- ческие задачи, относящиеся к вопросам массового обслуживания.

Введем необходимые понятия.

Потоком событий называется последовательность событий, кото- рые наступают в случайные моменты времени (поступление вызовов на АТС; испускание числа электронов катодом электронной лампы в течение времени t; распад радиоактивного вещества за время t и т.д.).

Интенсивностью потока называют среднее число событий, появ- ляющихся в единицу времени.

Свойство ординарности потока состоит в том, что вероятность появ- ления двух и более событий за промежуток времени t → 0 является бес- конечно малой величиной по сравнению с вероятностью появления одного события:

Pt, t +Δ t (1) >> Pt,t +Δ t (i), i > 1.

(5.12)

Свойство отсутствия последействия состоит в том, что вероятность появления k событий на непересекающихся интервалах времени

]t, t + t[, ]t + t, t +2 t [

(5.13)

не зависит от номера интервала в (5.13).

Если λ(t) = λ = const на любом интервале времени из (5.13), то поток называют стационарным.

Среднее число (МО) событий в потоке от момента времени t до мо- мента времени t + τ можно вычислить по формуле

t +τ
(t, t + τ) = ∫ λ(z) dz.	(5.14)
t
Для стационарного потока очевидно:
(t, t + τ) = λ τ.	(5.15)

5.7. Определение. Поток событий называется пуассоновским (про- стейшим), если он обладает свойствами стационарности, ординарности, отсутствия последействия.

Для простейшего потока с интенсивностью l легко найти вероят- ность Pt,t +τ (m) появления события m раз на интервале времени [t, t + t].

Для этого

разобьем

интервал

[t, t

+ t] на n равных частей:

k = [t +

t(k −1); t + Dt × k ], k =

;

Dt =

1, n

Пусть Xk

–

число событий, появившихся за интервал времени k . Тогда из

условия ординарности и D(t, t +

) = l ×

получаем закон распределения

СВ Xk (так как M(Xk ) = D(t, t +

) = l

1 - λτ

λτ

(5.16)

Из свойства отсутствия последействия вытекает, что вероятность по-

явления события на интервалах Dk и De постоянна и равна λτ . n

Поэтому по теореме Бернулли

P	(m) = C	m	(	λτ	m	(1	-	λτ	n−m	.	(5.17)
P	(m) = C	n	(	)		(1	-	)		.	(5.17)
t, t +τ		n		n				n
				n				n

Повторив преобразования после (5.7¢), получаем

	(m) »	(lt)m e−λτ
P			.	(5.18)

t, t +τ		m!

Этими рассуждениями доказана

5.8.Теорема. Пусть поток событий является пуассоновским с ин- тенсивностью l Тогда вероятность появления m событий за время t вы- числяется по формуле (5.18).

5.9.Пример. Среднее число вызовов, поступающих на АТС за 1 мин., равно 2. Найти вероятность того, что за 5 мин. поступит а) 2 вызо- ва; б) менее 2-х вызовов. Поток вызовов – простейший.

О. l = 2, t = 5, k = 2.

P (2) =	(10)2 × e−10	» 0,000025.
P (2) =		» 0,000025.
5	2!
	2!			10 × e−10
P (k < 2) = P (0) + P (1) = e−10			+	10 × e−10	» 0,000495. Ä.
P (k < 2) = P (0) + P (1) = e−10			+		» 0,000495. Ä.
5	5	5	1!
			1!

5.10. Теорема (локальная, Муавра – Лапласа). Если вероятность по- явления события A в каждом опыте постоянна и равна p, а n ® ¥, то

где x = k − n p . n p q

			1					1			× e−		x2
lim P (k ) =							×
													2


n→∞	n		n p q							2p
											x2				(5.19)
		1			1				× e−		x2			,	(5.19)
(P (k ) »		1		×	1						2	)
(P (k ) »				×							2	)
n		n p q				2p

Æ.

5.11. Замечание. Для функции j(x) =	1	× e

	2p
	2p

− x2

2 имеются спе-

циальные таблицы значений при положительных значениях аргумента x. Так как функция j(x) – четная, то j(x) = j(– x ).


	5.12. Пример. Вероятность поражения мишени стрелком при силь-
ном ветре – 0,2.		Найти вероятность того, что при 400 выстрелах он поразит
цель 80 раз.
	О. По (5.19)
P (80) »		1		× j(	80 - 400 × 0, 2	) =1/ 8 × j(0) =1/ 8 × 0,3989 = 0,04986.
P (80) »				× j(		) =1/ 8 × j(0) =1/ 8 × 0,3989 = 0,04986.
400	400	× 0, 2 × 0,8	20 × 0, 4
	400	× 0, 2 × 0,8	20 × 0, 4

Вычисления по формуле (5.1) дают Р400 (80) = 0,0498, но очень громоздки. 5.13. Теорема (интегральная, Муавра – Лапласа). Если вероятность появления события A в каждом опыте постоянна и равна p, а n ® ¥, то ве- роятность Pn (k1, k2) того, что в этих n опытах A появится не менее k1 раз и

не более k2 раз, вычисляется по формуле

<<< < Предыдущая 1 2 34 / 244 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб48умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб39умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб37умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб43умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб44умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб50умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб42умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб90умк_Яско_ Диф.уравнения_Ряды.pdf