
14-es_1 / Высшая математика (РТФ) / умк_Пальчик_Теория вероятностей
.pdf



16. Критерий проверки нулевой гипотезы. Область принятия гипотезы. Критерий согласия. Проверка гипотезы о распределении генеральной совокупности по закону Пуассона с помощью критерия Пирсона χ2 (хи-квадрат)
Статистической гипотезой называется всякое утверждение о пред- полагаемом законе неизвестного распределения или о параметрах извест- ного распределения.
Нулевой называется выдвинутая гипотеза, конкурирующей − гипоте- за, которая противоречит нулевой. В статистической оценке могут быть допущены ошибки.
Ошибка первого рода состоит в том, что будет отвергнута правиль- ная гипотеза.
Ошибка второго рода − в том, что будет принята неправильная ги- потеза. Вероятность совершить ошибку первого рода обозначается буквой α и называется уровнем значимости. Чаще всего уровень значимости при- нимают равным 0,05 или 0,01.
Статистическим критерием или просто критерием называют слу-
чайную величину К, которая служит для проверки нулевой гипотезы.
Эмпирическим значением критерия К называется значение критерия
Кв , вычисленное по выборке.
Критической областью называется совокупность значений крите- рия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезы (областью допустимых значений) на-
зывается совокупность значений критерия, при которых гипотезу прини- мают.
Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия: χ2 Пирсона, Колмогорова, Смирнова и другие.
Подробнее о применении распределения χ2 говорится в лекции 14.
Для проверки нулевой гипотезы по критерию Пирсона:
а) находятся эмпирические частоты mi ; б) вычисляются теоретические частоты
m′i = n·Pi , |
(16.1) |
где n = Σmi , Pi = P(x = i) – для дискретного распределения; Pi = P(xi ≤ x < xi+1) – для непрерывного распределения;
207

в) вычисляется статистика χ2эмп = Σ |
(mi - mi¢)2 |
; |
(16.2) |
|
|||
|
mi¢ |
|
|
г) по таблице критических точек распределения χ2 при уровне значи- |
|||
мости α и числе степеней свободы s = k – p – 1, где k – |
число различных |
||
групп выборки, p − число неизвестных параметров распределения, нахо- дится χ2теор (или χ2кр );
д) сравниваются χ2эмп и χ2кр ; если χ2эмп < χ2кр , нулевая гипотеза при- нимается, в противном случае − отвергается.
Для проверки гипотезы о распределении генеральной совокупности по закону Пуассона при уровне значимости α по критерию χ2 необходимо:
1.Найти по заданному эмпирическому распределению выборочную среднюю x и выборочную дисперсию σв2.
2.Сравнить x и σв2.
3.Принять в качестве оценки параметра λ распределения Пуассона
P (x = i) = li × e−λ |
(16.3) |
n
i!
выборочную среднюю λ = x .
4.Найти по формуле Пуассона (или по таблице прил. 6) вероятности Pi появления ровно i событий в n испытаниях (i = 0, 1, 2, ..., r, где r − мак- симальное число наблюдавшихся событий; n − объем выборки).
5.Найти теоретические частоты по формуле (12.1) и объединить ин- тервалы с частотами, меньшими пяти.
6.Сравнить эмпирические и теоретические частоты с помощью кри- терия Пирсона, приняв число степеней свободы s = k – p – 1, где k – число различных групп выборки, p = 1.
7.Сделать вывод о принятии или не принятии гипотезы о распреде- лении генеральной совокупности по закону Пуассона.
16.1.Пример. Используя критерий Пирсона, при уровне значимости
α= 0,05 проверить, согласуется ли гипотеза о распределении генеральной совокупности по закону Пуассона с эмпирическим распределением выбор- ки объема n = 200 (табл. 1):
Таблица 1
X |
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
m |
120 |
52 |
22 |
4 |
2 |
|
|
|
|
|
|
208

О. 1. Найдем выборочную среднюю и выборочную дисперсию по
формулам (12.1) и (12.2):
|
|
|
|
= |
1 |
(52 + 44 + 12 + 8) = 0,58; |
|
|
x |
||||||
|
|
|
|||||
|
200 |
|
|||||
σв2 = |
1 |
(52 + 4·22 + 9·4 + 16·2) – (0,58) 2 = 0,70. |
|||||
200 |
|||||||
|
|
|
|
|
|||
2.Выполнение с достаточно высокой степенью точности равенства
x≈ σв2 подтверждает правильность выбора нулевой гипотезы о распреде-
лении генеральной совокупности по закону Пуассонa.
3.Примем в качестве оценки параметра λ выборочную среднюю:
λ= 0,58. Следовательно, аналитическое выражение предполагаемого зако-
на Пуассона по формуле (16.3) имеет вид:
|
|
|
(x = i) = |
(0,58)i × e−0,58 |
|||||||
|
P |
|
|
|
|
|
. |
||||
|
|
|
|
|
|
||||||
|
200 |
|
|
|
|
i! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Положив i = 0, |
1, |
2, 3, |
4, найдем вероятности Pi появления ровно |
||||||||
i событий в 200 испытаниях: |
|
|
|
|
|
|
|
|
|
||
P = P |
(x = 0) = |
(0,58)0 × e |
−0,58 |
||||||||
|
|
|
|
=0,5599; |
|||||||
|
|
|
|
||||||||
0 |
200 |
|
|
|
|
|
0! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = P |
(x =1) = |
(0,58)1 × e−0,58 |
= 0,3247. |
||||||||
|
|||||||||||
1 |
200 |
|
|
|
|
|
1! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, Р2 = 0,0942; |
Р3 = 0,0182; |
Р4 = 0,0026. |
|||||||||
5. Найдем теоретические |
частоты по формуле (16.1) m′i = n·Pi ; |
||||||||||
m′0 = 111,98; m′1 = 64,94; m′2 = 18,84; m′3 = 3,64; m′4 = 0,52.
6. Для сравнения эмпирических и теоретических частот по критерию Пирсона составим расчетную таблицу (табл. 2), предварительно объединив малочисленные частоты (4 + 2 = 6; i = 4, соответствующее частоте m = 2,
считается случайным и исключается из рассмотрения) и соответствующие им теоретические частоты (3,64 + 0,52 = 4,16).
209

|
|
|
|
|
|
|
|
Таблица 2 |
|||
|
|
|
′ |
′ |
′ |
2 |
|
(m - m¢)2 |
|
||
|
|
|
|
i |
i |
|
|||||
|
i |
mi |
m i |
mi − m i |
(mi − m i) |
|
|
|
|
|
|
|
|
mi¢ |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
120 |
111,98 |
8,02 |
64,3204 |
|
|
0,5744 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
52 |
64,94 |
−12,94 |
167,4436 |
|
|
2,5784 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
22 |
18,84 |
3,16 |
9,9856 |
|
|
0,5300 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
6 |
4,16 |
1,84 |
3,3856 |
|
|
0,8138 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Σ |
200 |
|
|
|
|
|
χ2эмп=4,50 |
|
||
|
|
|
|
|
|
|
|
||||
|
7. По таблице критических точек распределения χ2 при уровне зна- |
||||||||||
чимости α = 0,05 и числе степеней свободы s = k – p – 1 = 4 − 2 = 2 |
нахо- |
||||||||||
дим χ2кр(0,05; 2) = 6,0. Так как χ2эмп < χ2кр , нет оснований отвергнуть гипо- тезу о распределении генеральной совокупности по закону Пуассона. Ä.
16.2. Пример. В результате натурного обследования автостоянки од- ного из супермаркетов в г. Минске получены данные о прибытии легковых машин к месту парковки в интервале 15 мин. Определить основные харак- теристики эмпирического распределения и установить теоретический за- кон, который характеризует число прибывающих автомашин за период ∆t = 15 мин. Результаты обследования представлены в табл. 3.
Таблица 3
xi |
0 |
1 |
2 |
3 |
|
|
|
|
|
mi |
26 |
14 |
4 |
6 |
|
|
|
|
|
Здесь xi − число автомашин, mi − число интервалов ∆t = 15 мин, в ко- торые наблюдалось xi машин, объем выборки n = 50.
О. Средняя выборочная и выборочная дисперсия равны:
|
|
= |
1 |
(14 + 8 + 18) = 0,80; |
σв2 = |
1 |
(14 + 4·4+ 9·6) − (0,80) 2 = 1,04. |
|
x |
||||||||
|
|
|
||||||
50 |
|
50 |
|
|||||
Равенство x ≈ σв2 является первым признаком того, что анализируе- мая случайная величина может быть подчинена закону Пуассона.
Параметр λ = x = 0,8 и аналитическое выражение закона Пуассона имеет вид:
P (x = i) = |
(0,8)i × e |
−0,8 |
|
|
|
. |
|
|
|
||
50 |
i! |
|
|
|
|
|
|
210


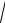

 10ε ). = 0,475.
10ε ). = 0,475. 


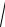 ((2
((2