14-es_1 / Высшая математика (РТФ) / умк_Пальчик_Теория вероятностей

13.5. Пример. СВ Х имеет нормальное распределение. По результа- там наблюдавшихся значений (13.1) этой СВ оценить параметры m и s нормального распределения.

Из формул (13.12) и (13.13) видно, что эмпирические моменты вы- числяются по данным наблюдений xi.

Неизвестный закон распределения в нашем случае можно записать в виде плотности распределения

Таким образом, метод моментов состоит в составлении (и решении) системы уравнений

n1(Q1,K, Qr ) = n1 (Q1,K, Qr )

LLLLLLLLLLLLL , k ³ r , (13.18)

nk (Q1,K, Qr ) = nk (Q1,K, Qr )

и аналогично

13.6. Пример. Пусть СВ Х распределена по показательному закону с плотностью распределения f(x, Q) = Qe-Θx, x ³ 0. (Здесь Q1 = Q, r = 1).

По результатам выборки x1, ..., xn оценить Q.

О. По методу моментов (13.18) достаточно составить одно уравнение

1 = (по частям) = Q .

n1 = (по (13.12) = xB = 1 ∑n xi . n i =1

Поэтому (13.20) дает нам Q1 = xB .

Ответ: Q = 1 . Ä. xB

Метод наименьших квадратов

Пусть требуется оценить величину Х по результатам n измерений

xi = Q + ei , i =1, n,

где ei – ошибки измерений, Q – точное значение Х.

Метод наименьших квадратов (МНК-метод) состоит в том, что на-

ходят точечную оценку Q величины Q, которая минимизирует функцию

то есть минимизирует сумму квадратов отклонений данных выборки от точного значения Q величины Х.

13.7. Пример. МНК-методом найти оценку Q выборочного среднего x0 генеральной совокупности по выборке {x1,..., xn}.

n

О. Составим функцию U (Q) = ∑(xi - Q)2.

i=1

103

14.Распределение χ2 (хи-квадрат) и его значение в МС. Распределение Стьюдента и его значение в МС.

Распределение Фишера и его значение в МС

Пусть СВ Y Î N(m, s). Тогда СВ U = Y −sm называется стандарти-

зированной СВ (по отношению к Y). Как показано в лекции 10 (см. (10.22),

UÎ N(0, 1).

14.1.Определение. Квадрат стандартизированной СВ

называется случайной величиной c2 (хи-квадрат) с одной степенью свободы.

Если рассматривать n независимых СВ Y1,..., Yn, где Yi Î N(mi, si ), i =1, n, то сумма квадратов их стандартизированных величин

104

В МС изучена (К. Пирсоном) плотность распределения f (χ2n ) СВ χ2n . f (χ2n ) является неэлементарной функцией от числа ν степеней свободы.

Ее явное выражение можно найти, например, в [3, (19.28), c. 144].

Для практических специалистов, как правило, достаточно использо-

вать квантили χ2n -распределения.

14.2. Определение. Квантилью, соответствующей вероятности α, на- зывается такое значение СВ X, X = xα, при котором

xα

где f(x) – плотность распределения СВ Х.

С геометрической точки зрения нахождение квантили xα заключается в таком выборе значения X = xα, при котором площадь криво- линейной трапеции правее прямой X = xα (рис. 14.1) была бы равна α. Поэтому квантили xα и x1-α называются симметрическими. Если график f(x) симметричен относительно прямой x = 0, то xα = – x1-α.

f(x)

S=α

Рис. 14.1

Из формулы (4.5) следует, что для квантилей xα и xβ имеет место формула

105

Для χ2n -распределения с n степенями свободы квантиль, соответст-

вующая вероятности a, обозначается

Значение c2-распределения в МС показывает следующая теорема.

14.3. Теорема. Пусть X1, ..., Xn – независимые СВ, Xi Î N (m, s), i =1, n .

Тогда СВ

все части этого неравенства на n/s2, получаем a n / s2 £ SX2 n / s2 £ b n / s2 и

применяем формулу (14.5) для c2-распределения ввиду теоремы 14.3. Получаем

c2-распределение применяется также при проверке статистических гипотез, что будет рассмотрено далее.

называется безразмерной дробью Стьюдента (псевдоним английского статистика В.С. Госсета (1886 – 1937) с n степенями свободы, где

106

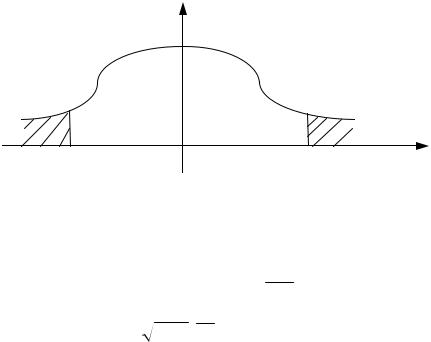
Стьюдентом изучена плотность распределения f(t) СВ t и показано, что она зависит только от одного параметра n – числа степеней свободы. Им же изучен график функции f(t), который при любом n симметричен от- носительно оси ординат. При n → ∞ f(t) → N(0,1). На практике уже при n > 30 f(t) заменяют нормальным распределением N (0,1).

На практике используются квантили t-распределения tα / 2; n в зависи-

мости от числа степеней свободы n и заданной вероятности доверия α .

Числа tα / 2; n находятся из решения уравнения

tα / 2; n

Сгеометрической точки зрения нахождение квантилей заключается

ввыборе такого значения t = tα / 2; n , при котором суммарная площадь за-

штрихованных криволинейных трапеций (рис. 14.2) была бы равной α. Для квантилей t-распределения имеются специальные таблицы значе-

ний, поскольку решение уравнений (14.10) достаточно сложная процедура.

f(t)

Значение t-распределения в МС показывают следующие две теоремы. 14.5. Теорема. Пусть X1, ..., Xn – независимые СВ, распределенные

нормально с M(Xi ) = m и D(Xi ) = σ2 для всех i = 1, n . Тогда СВ

T = 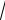n −1(xB − m) / SX ,

107

14.6. Теорема. Пусть из двух нормально распределенных ГС с оди- наковым средним квадратическим отклонением сделаны две независимые

где m1 и m2 – математические ожидания первой и второй ГС соответственно, имеют распределение Стьюдента с n = n1 + n2 – 2 степенями свободы. Æ.

Пусть СВ X1, ..., Xm; Y1, ..., Yn – независимы и

14.7. Определение. Безразмерная СВ

j =1

где U и Z имеют c2-распределения соответственно с m и n степенями сво-

боды, называется безразмерной дробью Фишера.

Фишер нашел выражение для плотности распределения f(F) = j(n1, n2), где n1 = m, n2 = n и применил СВ F для сравнения дисперсий генеральных совокупностей, распределенных нормально, на основании сделанных из них выборок.

А именно, имеет место

14.8. Теорема. Пусть S12 и S 22 – исправленные выборочные диспер- сии, определенные из выборок объемов n1 и n2, взятых из нормально рас- пределенных ГС с одинаковыми средними квадратическими отклонения-

.

108

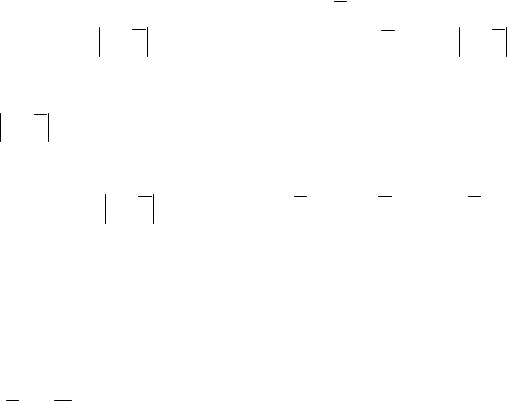
Значения квантилей F-распределения Fα; ν1; ν2 в зависимости от чис-

ла степеней свободы ν1, ν2 и от заданной вероятности α находятся из уравнения

Ввиду сложности решения этого уравнения созданы специальные таблицы значений Fα; ν1; ν2 .

15. Интервальные оценки параметров распределения. Доверительная вероятность. Доверительный интервал. Уровень значимости. Доверительный интервал для m, где X N(m, σ), σ − известная величина. Доверительный интервал для m,

где X N(m, σ), σ − неизвестная величина

После получения точечной оценки Θ параметра Θ возникает вопрос о величине Θ − Θ , т.е. о надежности оценки Θ . Если Θ − Θ < δ → 0 , то

оценка считается надежной.

Другими словами, возникает вопрос о вероятности события

Θ − Θ < δ , где δ − наперед заданное положительное число, желательно

малое.

P( Θ − Θ < δ) = P(−δ < Θ − Θ < δ) = P(Θ − δ < Θ < Θ + δ). (15.1)

Для ответа на этот вопрос заранее выбирают необходимую для су- щества дела доверительную вероятность 1 – α и проверяют выполнение соотношения

]Θ − δ, Θ + δ[ является доверительным, так как точное значение параметра

109

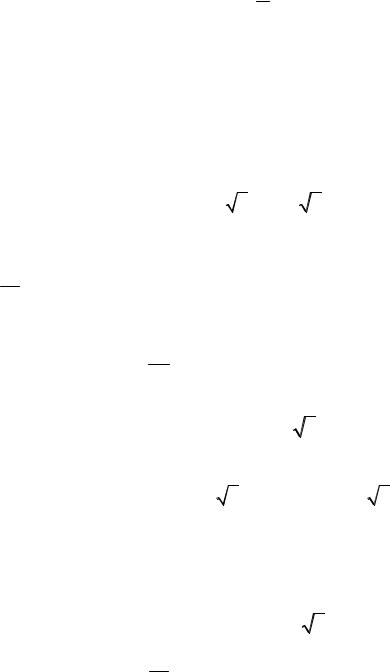
Θ попадает в этот интервал с требуемой доверительной вероятностью (на-

дежностью) 1 – α.

Число α называют коэффициентом доверия или уровнем значимости.

На практике обычно α {0,1; 0,05; 0,01}, что соответствует 90-, 95- и 99 %-ным доверительным интервалам соответственно.

Если число δ велико, то оценка Θ считается «плохой».

15.1. Теорема. Предположим, что СВ X N(m, σ), σ − известная ве- личина. Пусть имеется выборка

является доверительным для m с надежностью 1 – α = 2Ф(ε).

О. Из 12.12, 12.14, 12.16 следует, что в качестве оценки для m можно

взять xB .

По соглашению 11.1 выборку (15.3) можно рассматривать как реали- зацию СВ (X1,..., Xn), у которой компоненты Xi являются независимыми и Xi N(m, σ) для всех i = 1, n .

По теореме 12.6