
14-es_1 / Высшая математика (РТФ) / умк_Пальчик_Теория вероятностей
.pdfМетодом экспертных оценок пользуются, например, при судействе фигурного катания, при заключении торговых сделок и т.д.
На основании аксиом 1К – 3 К легко получаются следующие форму- лы для вычисления вероятностей событий А, В:
Если A Í B, то
P(A) ≤ P(B). |
(2.7) |
||
P(B – A ) = P(B) – P (A). |
(2.8) |
||
P(Ο/) = 0 (вероятность невозможного события – нуль). |
(2.9) |
||
P( |
|
=1 - P( A). |
(2.10) |
A) |
|||
2.7. Теорема (сложения) |
|
||
P(A È B) = P(A) + P(B) – P (A Ç B). |
(2.11) |
||
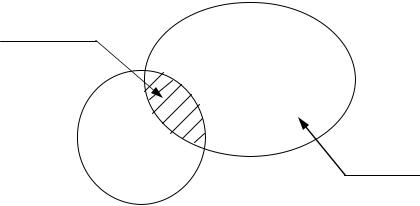
О. Если А и В несовместимы, то (2.11) следует из аксиомы 3К. Если |
|||
же А и В совместимы (рис. 2.2), то |
|
||
A È B = A È (B – A ), |
(2.12) |
||
где А и В – А несовместимы. |
|
||
Аналогично |
|
||
B = (A Ç B) È (B – A ). |
(2.13) |
||
К равенствам (2.12) и (2.13) применяем аксиому 3К. Получаем
P(A È B) =P(A) + P(B – A ). |
(2.14) |
P(B) = P(A Ç B) + P(B – A ). |
(2.15) |
Вычитая почленно из (2.14) равенство (2.15), получаем (2.11). Ä.
21
A ÇB
B
A |
B − A |
Рис. 2.2
2.8. Определение. (Статистическое определение вероятности). Под вероятностью события А при этом подходе понимается величина
P( A) = lim |
m |
, |
(2.16) |
|
|||
n→∞ n |
|
||
т.е. относительную частоту события принимают за оценку вероятности по- явления события А.
3. Условная вероятность. Независимость событий. Исчисление вероятностей событий (умножение). Формула полной вероятности. Формула Байеса
3.1.Определение. Пусть Е – в.э. и (W , F, P) – его вероятностная модель. Предположим, что нас интересует вероятность появления события
Авнутри события В. Тогда такая вероятность события А называется услов- ной вероятностью А (относительно события В) и обозначается Р(А/В).
3.2.Теорема.
|
|
|
P(A/B) = P(A Ç B) / P(B). |
(3.1) |
||||
О. (Случай, когда |W| < ¥). Пусть |W| = n, событию А благоприятст- |
||||||||
|
исходов ( A = {wi , i = |
|
}) , событию В – |
|
|
|
||
вуют r |
1, r |
m исходов |
||||||
(B = {w j , |
j = |
|
}) , а событию A Ç B – k исходов ( A Ç B = {wl , l = |
|
}). |
|||
1, m |
1, k |
|||||||
22

Тогда P(B) = m/n, P(A Ç B) = k/n, P(A/B) = k/m. Тогда
P( A / B) = k = k / m = P( A Ç B) . Ä.
|
m |
m / n |
P(B) |
||||
3.3. Пример. Е – бросание шестигранной игральной кости и под- |
|||||||
счет числа выпавших очков. Событие А – |
выпадает число очков больше |
||||||
трех: A = {w4, w5, w6}. P( A) = |
| A | |
= |
3 |
= |
1 |
. Пусть известно, что произошло |
|
|
6 |
|
|||||
|
| W | |
2 |
|
|
|||
событие В, состоящее в том, что выпало четное число очков: B={w2,w4, w6}. Вероятность события А при условии, что оно появляется внутри события
В, равна 2/3, т.е. Р(А/В) = 2/3.
3.4.Теорема (умножения)
P(A Ç B) = P(A) P(B/A) = P(B) P(A/B). |
(3.2) |
О. Применяем теорему 3.2 к вычислению Р(А/В) и Р(В/А). Использу- ем очевидный факт, что P(A Ç B) = P(B Ç A). Ä.
3.5. Теорема. P(A Ç B Ç C) = P(A) P(B/A) P(C/A Ç B).
О. Используем 2 раза теорему 3.4. Ä.
Используя метод математической индукции, теорему 3.5 можно рас- пространить и на n < ¥ сомножителей.
3.6. Определение. События А и В независимы, если появление со- бытия В не меняет вероятности события А, и наоборот, т.е.
Р(А) = Р(А/В)
Р(В) =Р(В/А) или
P(AB) = P(A) × P(B). |
(3.3) |
Отметим, что из (3.3) и (3.2) следует, что если А не зависит от В, то и
Вне зависит от А.
3.7.Определение. События {Ai , i =1, n} называют попарно незави- симыми, если любая их пара независима.
События {Ai , i =1, n} называют независимыми в совокупности, если для любых k из них (k £ n), выполняется соотношение
P( A Ç A ÇKÇ A ) = Пk |
P( A |
). |
(3.4) |
||
1 2 |
k |
j=1 |
j |
|
|
23

3.8.Теорема. Если А и В – независимые события, то 1) А и B ;
2)A и B; 3) A и B – независимы. Æ.
3.9.Теорема. Вероятность совместного появления нескольких со- бытий, независимых в совокупности, равна произведению вероятностей этих событий, т.е.
P(A1 × A2 … A n) = P(A1) × P(A2) … P (An).
О. Легко следует из (3.4). Ä.
3.10. Теорема. Вероятность появления хотя бы одного из событий, независимых в совокупности, равна разности между 1 и произведением вероятностей событий, противоположных данным, т.е.
P( A1 + A2 +K + An ) =1 - P( |
A1 |
) × P( |
A2 |
)KP( |
An |
). |
(3.5) |
||||||
О. Событие |
|
× |
|
K |
|
– совместное «не появление» |
|
||||||
A1 |
A2 |
An |
событий |
||||||||||
A1,…,A n. Оно противоположно событию A = A1 + A2 + … + A n. Поэтому
P( A) + P( A1K An ) =1. Ä.
3.11.Пример. Вероятность попадания в цель стрелком № 1 равна р1
=0,9; стрелком № 2 – р2 = 0,85. Какова вероятность поражения цели (хотя бы одно попадание) при их залпе?
О. q1 =1 - 0,9 = 0,1; q2 = 0,15. По (3.5) 1 - q1 q2 =1 - 0,015 = 0,985. Ä.
3.12. Теорема (формула полной вероятности). Вероятность события А, которое может появиться вместе с появлением только одного из несо- вместимых событий B1, …, B n, с известными вероятностями, образующими полную группу, вычисляется по формуле
P(A) = P(B1) × P(A/B1) + … + P (Bn) × P(A/Bn). |
(3.6) |
О. По условию А наступит, если наступит одно из несовместимых со- бытий B1,…,B n, т.е. А появится, если появится одно из событий: B1 A,…,B nA. Или A = B1 A + …+ B n A. По условию теоремы Bi A Ç B j A = O/ , при i ¹ j. По аксиоме 3К P( A) = P(B1A) +K + P(Bn A) = (по (3.2) =
= P(B1)P( A / B1) +K + P(Bn )P( A / Bn ). Ä.
24

3.13. Пример. На фабрике 30 % продукции делает цех № 1, 25 % – цех № 2, 45 % – цех № 3. Цех № 1 дает 1 % брака, цех № 2 – 1,2 %, цех № 3 – 2 %.
Какова вероятность того, что наугад выбранная единица продукции завода – бракованная (событие А); какова вероятность того, что наугад вы- бранная бракованная единица продукции сделана в цехе № 3? (В3 /А)?
О. Пусть А – событие, состоящее в выборе бракованной единицы продукции, Вi – событие, состоящее в том, что единица продукции изго- товлена в цехе № i, i = 1, 2, 3. Тогда на 1-й вопрос получаем ответ:
А появится или вместе с В1, или вместе с В2, или вместе с В3. По формуле
(3.6) имеем
3 |
|
|
|
|
|
P( A) = ∑P(Bi )P( A / Bi ) = 0,3 |
× 0,01 + 0,25 |
× 0,012 |
+ 0, 45 × 0,02 |
= 0,015. |
Ä. |
i=1 |
|
|
|
|
|
Иногда при условиях, указанных в теореме 3.12, интересуются дру- гим вопросом: до эксперимента были известны P(Bi ), i =1, n , а каковы ве- роятности событий Bi , i =1, n после появления события А? Другими сло- вами, каковы P(Bi / A), i =1, n ? Ответ имеется в следующей теореме.
3.14. Теорема (формула Байеса). При условиях теоремы 3.12 веро- ятность события (Bi / A) после проведения эксперимента и появления со- бытия А вычисляется по формуле
|
P(B / A) = |
P(Bi ) × P( A / Bi ) |
, |
|
(3.7) |
||||
|
|
|
|
|
|||||
|
|
i |
P( A) |
|
|
||||
|
|
|
|
|
|
||||
где Р(А) вычисляется по формуле (3.6). |
|
|
|
|
|
|
|||
О. P(ABi) =P(A)P(Bi /A)=P(Bi)P(A/Bi). Откуда и следует (3.7). |
Ä. |
||||||||
3.15. Пример. Теперь мы можем ответить на второй вопрос в при- |
|||||||||
мере 3.13. А именно, |
|
|
|
|
|
|
|
|
|
P(B / A) = |
P(B3 ) × P( A / B3 ) |
= |
0,45 × 0,02 |
= 0,6. |
|
||||
|
|
|
|||||||
3 |
|
P( A) |
0,015 |
|
|
||||
|
|
|
|
||||||
Таким образом, до эксперимента Р(В3) = 0,45, а после эксперимента и наступления события А Р(В3 /А) = 0,6.
Формулы Байеса (3.7) позволяют переоценивать вероятности собы- тий (гипотез) после получения добавочной информации в ходе в.э.
25
4. Понятие случайной величины (СВ). Дискретная и непрерывная СВ.
Понятие о законах распределения СВ. Функция распределения. Плотность распределения
Пусть Е – в.э. (Ω, F, P) – его математическая модель (ММ). Предпо- ложим, что каждому элементарному событию (э.с.) w Ω ставится в соот- ветствие действительное число X(w). Другими словами, результаты экспе- римента записываются с помощью чисел. Если изменяется w, то изменяет- ся и X(w).
Фактически мы имеем некоторую функцию X(w), определенную на множестве Ω. Если w пробегает множество Ω, то X(w) пробегает некоторое множество значений, которое условимся обозначать ΩX.
Для того чтобы перевести модель (Ω, F, P) на числовой язык, нужна некоторая новая «числовая» модель (ΩX, FX, PX). Мы уже знаем, что FX должна быть σ-алгеброй для ΩX (по определению модели в.э. и определе- нию 1.14). FX состоит из событий (подмножеств из ΩX). Как и в 1.4, здесь события состоят из элементарных событий из ΩX. Однако понятие э.с. в ΩX требует уточнения.
4.1. Определение. Пусть (Ω, F, P) – модель в.э. Е, Х – действитель- ная функция, определенная на Ω, x R.
Если wi Ω и X(wi) = x, то х назовем образом wi в ΩX, а wi – прообра-
зом х в Ω.
Элементарным событием в ΩX назовем образ элементарного собы- тия w Ω, т.е. число х (точку х).
Сложное событие в ΩX – это совокупность элементарных событий (точек), т.е. подмножество в ΩX.
Если В – событие в ΩX, то прообразом В в Ω называется событие
X −1(B) = {wi Ω / X (wi ) B}.
Теперь можно дать строгое определение СВ Х.
4.2.Определение. Пусть (Ω, F, P) – модель в.э. Е.
Случайной величиной Х называется действительная функция X(w), отображающая Ω в ΩX R так, что прообразы событий из FX лежат в F, т.е. являются событиями из F.
26

Можно пользоваться и более простым определением СВ.
4.2′. Определение. СВ называют величину, которая в результате единичного испытания принимает единственно возможное значение, не известное заранее.
Заметим, что σ-алгебра для ΩX определяется как и в 1.14.
Отметим, что если ΩX состоит из счетного числа отдельных элемен- тов, то ΩX называют дискретным множеством, а СВ Х называют дискрет- ной СВ. Если же ΩX заполняет сплошь некоторый действительный интер- вал [α, β], то ΩX называют непрерывным множеством на интервале [α, β], а
Х– непрерывной СВ.
4.3.Пример. Пусть Е – двукратное подбрасывание монеты. Тогда
Ω = {(г, г), (г, ц), (ц, г), (ц, ц)} – множество всех мыслимых исходов. Рассмотрим числовую функцию Х (или СВ Х) (число выпадений гер-
ба), определенную на множестве Ω. Тогда
ΩX = {0, 1, 2} – герб может выпасть 0, 1, 2 раза. Таким образом, Х: Ω → ΩX можно задать в виде таблицы (X – дискретная СВ).
w Ω |
(г, г) |
(г, ц) |
(ц, г) |
(ц, ц) |
|
|
|
|
|
X(w) = x |
2 |
1 |
1 |
0 |
|
|
|
|
|
4.4.Пример. В квадрат {0 ≤ x ≤ 1, 0 ≤ y ≤ 1} бросается точка. Тогда
Ω= {w = (x, y) / 0 ≤ x ≤ 1, 0 ≤ y ≤ 1} – множество координатных пар для точек квадрата. Рассмотрим СВ Х: расстояние от начала координат до точки падения. Тогда точке w = (x, y) ставится в соответствие по закону Х
действительное число X (w) = x2 + y2. Откуда Ω |
|
= [0, |
|
|
X |
2]. Таким обра- |
|||
|
|
|
|
|
зом, Х – непрерывная СВ. |
|
|
|
|
После введения СВ Х нужно ввести вероятности, с которыми Х при- |
||||
нимает свои значения. Тогда мы будем иметь и третью компоненту РХ в модели (ΩX, FX, PX). То есть нам нужно указать способ вычисления вероят- ностей наступления событий из класса FX. Этот способ простой: вероят- ность события B FX должна равняться вероятности события X-1(B) F (т.е. события, являющегося прообразом в F для В из FX ).
Итак,
PX (B FX ) = P(X-1 (B) F) B FX . |
(4.1) |
27

4.5. Определение. Всякое соотношение, устанавливающее связь между возможными значениями СВ и их вероятностями, называется зако-
ном распределения СВ.
4.6.Пример. Пусть E, W, X(w) как в 4.3. Тогда РХ (Х = 0) = (по (4.1)
=Р(Х -1(0)) = Р(ц, ц)) = 1 × 1 = 1 .
2 2 4
РХ (Х = 1) = Р(Х -1(1)) = Р((г, ц) или (ц, г)) = Р{(ц, г) + (г, ц)} =
= Р(г, ц) + Р(ц, г) = Р(г) Р (ц) + Р(ц) Р(г) = 1 × 1 + 1 × 1 = 1 .
|
|
|
|
2 |
2 |
2 |
2 |
2 |
||
РХ (Х = 2) = Р(Х -1(2)) = Р(г, г) = |
1 |
× |
1 |
= |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
2 |
4 |
|
|
|
|
|
|||
Таким образом, имеем следующий закон распределения вероятно- стей СВ Х из примера 4.3:
X(w) = x |
|
2 |
|
1 |
|
0 |
|
|||
PX (X) = P(X -1) |
|
1 |
|
|
1 |
|
|
1 |
|
(4.2) |
|
|
4 |
|
|
2 |
|
|
4 |
|
|
Из этого примера видно, что закон распределения дискретной СВ удобно задавать с помощью таблицы: под каждым значением СВ пишется вероятность того, что Х приняла это значение.
При этом закон распределения считается заданным, если в первой строке указываются все возможные значения дискретной СВ, т.е. полная группа событий WX.
WX |
x1 |
x2 |
... |
xn |
|
PX |
p1 |
p2 |
... |
pn |
(4.3) |
Тогда для второй строки таблицы (4.3) по аксиоме 3К имеем:
n |
= 1. |
|
∑pi |
(4.4) |
i=1
Для непрерывной СВ нужна более общая форма закона распределения.
28
4.7. Определение. Функцией распределения СВ Х называется функ- ция действительного переменного FX (x), определяющая вероятность того, что в результате эксперимента СВ X примет значение, меньшее некоторого
фиксированного числа x Î R, |
|
|
|
FX (x) = P(X < x) = P(X Î ]-¥, x[). |
(4.5¢) |
Если понятно, о какой СВ Х, Y или Z идет речь, то пишут F(x) вместо |
||
FX (x), FY (x), FZ (x). |
|
|
4.8. Теорема. F(x) обладает следующими свойствами: |
|
|
1°. |
lim F (x) = F (−∞) = 0. |
|
|
x→−∞ |
|
2°. |
lim F (x) = F (∞) = 1. |
|
|
x→∞ |
|
3°. x2 > x1 F(x2 ) ³ F(x1). |
|
|
4°. |
lim F (x) = F (x0 ) (непрерывность слева). |
|
|
x→ x0 −0 |
|
О. Свойства 1° и 2° очевидны из определения 4.7; 3° следует из свойства вероятностной меры: если A B, то P(A) ≤ P(B). В нашем случае
] - ¥, x1[Ì] - ¥, x2[ и P(-¥ < X < x1) £ P(-¥ < X < x2 ) , или
F (x1) £ F (x2 ). Ä.
4° примем без доказательства.
4.9.Теорема. Пусть F(x) – функция распределения СВ Х. Тогда
P(a ≤ X < b) = F(b) – F (a);
|
[a, b[ R. |
(4.5) |
|
|
|
О. Ясно, что события |
X Î] - ¥, a[ и X Î[a, b[ |
несовместимы, и |
(-¥ < X < a) È (a £ X < b) = (-¥ < X < b). Поэтому по аксиоме 3К |
||
P(-¥ < X < a) + P(a £ X < b) = P(-¥ < X < b). Откуда |
|
|
F (a) + P(a £ X < b) = F (b). Ä. |
|
|
4.10. Следствие. |
|
|
|
P(X = a) = 0. |
(4.6) |
О. Положим в (4.5) b = a. |
Ä. |
|
29

Геометрический смысл F(x) состоит в том, что она выражает вероят- ность того, что СВ Х примет значение, которое изображается на числовой оси точкой, расположенной левее х.
F(x) не дает представления о характере закона распределения СВ Х в достаточно малой окрестности точки x ΩX.
4.11. Определение. Средней вероятностью на отрезке [x, x + x] на- зывается отношение
|
|
P(x ≤ X < x + |
x) |
= по (4.5) = |
F (x + x) − F (x) |
. |
(4.7) |
|||
|
|
x |
|
|
||||||
|
|
|
|
|
|
x |
|
|||
|
Предположим, что F(x) дифференцируема на ΩX. Тогда из (4.7) имеем: |
|||||||||
|
|
lim |
F (x + x) − F (x) |
= F '(x )= f (x ). |
(4.8) |
|||||
|
|
|
||||||||
|
|
x→0 |
|
x |
|
|
|
|
|
|
|
4.11. Определение. Функцию f(x) называют плотностью распреде- |
|||||||||
ления вероятностей СВ Х, |
а ее график – |
|
кривой распределения. Перепишем |
|||||||
(4.8): |
F ≈ F '(x ), или |
|
|
|
|
|
|
|
||
|
x |
|
|
|
|
|
|
|
||
|
|
|
P(x ≤ X < x + |
x) ≈ f (x) dx. |
(4.9) |
|||||
Правая часть (4.9) отличается от левой так, как заштрихованный прямоугольник на рис.4.1 – от соответствующей криволинейной трапеции.
y
y=f (x)
0 |
x |
x |
x+ x |
|
Рис. 4.1 |
30
