Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Пальчик_Теория вероятностей

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2412 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Заметим, что

M (Y ) = M (

× (

- m)) =

M (

- m) =

(M (

) - M (m)) =

= (15.5) =

(m - m) = 0.

D(Y ) =

D(xB

- m) =

(D(xB ) - 0) = (15.5) =

=1.

При вычислении M(Y) и D(Y) мы пользовались свойствами матема- тического ожидания и дисперсии из 6.13 и 6.14.

Таким образом, Y Î N(0,1). Но тогда по теореме 7.8 для любого e > 0

имеем P(|Y| < e) = 2Ф(e). По (15.6) тогда

- m

) = 2Ф(e).

- m

< e) = P(

Из условия теоремы следует, что решив уравнение 1 – a = 2Ф(e),

можно найти значение e, при котором выполняется равенство

P( xB - m < εσ ) =1 - a. n

То есть с доверительной вероятностью 1 – a = 2Ф(e) можно утвер-

ждать, что интервал (15.4) является доверительным для оценки m. Ä. 15.2. Пример. Глубина дорожки, оставляемой подшипником, изме-

ряется оптическим глубиномером, систематическая ошибка (одного знака) которого равна 0. Случайные ошибки измерения глубины распределены нормально с s = 20 мкм. Сколько надо сделать измерений, чтобы ошибка измерения была не более 15 мкм с надежностью 0,9?

О. Ошибка - это отклонение xB - m . По условию xB - m £15, s = 20 . При надежности 0,9 имеем уравнение 2Ф(e) = 0,9 и по таблицам значений функции Лапласа находим e = 1,645. Ввиду (15.4)

111

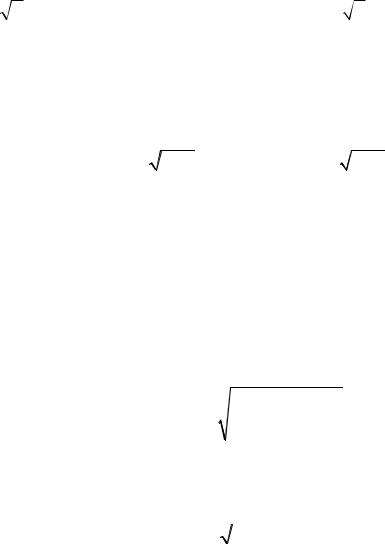
ошибка (εσ / 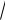n ) ≤ 15 (по условию). Откуда 1,645 × 20 / 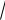n £15 или n > 4.

Достаточно сделать n = 5 измерений. Ä.

15.3. Теорема. Предположим, что СВ X Î N(m, s) и s - неизвестная величина. Пусть имеется выборка (15.3) значений X и задана вероятность

1 – a. Тогда интервал

- tα / 2;n-1 × SX /

n -1;

+ tα / 2;n-1 × SX /

n -1

(15.7)

tα / 2;n-1

является доверительным для m

с надежностью 1 - a = 2

∫

f (t) dt ,

где

SX2 - выборочная дисперсия,

- выборочная средняя,

f(t)

- плотность

вероятности t-распределения.

О. На основании выборки (15.3) и можно найти точечные оценки

неизвестных параметров

)2 / n

= s

∑(x -

= S

i=1

Рассмотрим вспомогательную СВ

t =

- m

n -1.

(15.8)

По теореме 14.5 ввиду соглашения 11.1 СВ t из (15.8) имеет распре-

деление Стьюдента с n = n – 1

степенями свободы.

Вероятность того, что СВ t попадает в интервал

-tα / 2;n-1; tα/2;n-1 ,

ввиду (14.10) вычисляется по формуле

< tα / 2;n-1) =1 - a .

(15.9)

Так как 1 – a задано по условию теоремы, то квантили ±tα / 2;n-1

мо-

tα / 2;n-1

f (t) dt =1 - a ,

гут быть найдены или из решения уравнения

2 ∫

или

приближенно по таблицам квантилей t-распределения (см. рис. 14.2).

112

Из (15.9) и (15.8) после преобразований имеем:

P(-tα / 2;n-1 <

(

- m) ×

n -1

< tα

= P(-tα / 2;n-1

< (xB

- m) <

n -1

= P(xB - tα / 2;n-1 ×

< m < xB

n -1

Ä.

/ 2;n-1) =

tα./ 2;n-1 ×	SX		) =

	n -1
	n -1
+ tα / 2;n-1 ×		SX		)	=1 - a.


		n -1

15.4. Пример. Измерили диаметры четырех однотипных подшип- ников и получили данные: x1 = 0,25; x2 = 0,24; x3 = 0,26; x4 = 0,25. Найти до- верительный интервал для истинного диаметра d подшипников с надежно- стью 1 – a = 0,95, считая распределение результатов измерений d нор- мальным.

О. По условию задачи xB = 1 × (0, 25 + 0,24 + 0,26 + 0,25) = 0, 25 . По 4

формуле (12.6) вычисляем выборочное среднее квадратическое отклоне- ние SX = 0,082. Уровень значимости a = 0,05. По таблицам квантилей t-распределения находим t0,025;3 = 3,182, так как n – 1 = 3. По (15.7) находим

SX	×t0,025;3		=	0,082 ×3,182	» 0,14 . По (15.7)	искомый доверительный интер-

		n -1		3

вал есть ]0,25 – 0,14; 0,25 + 0,14 [ = ]0,11; 0,39[. Т.е. можно утверждать, что примерно в 95 % случаев dÎ]0,11; 0,39[. Ä.

16. Функциональная и статистическая зависимость между СВ. Линейная корреляция и свойства коэффициента

линейной корреляции. Уравнение линейной регрессии

Пусть X и Y - СВ. X и Y могут быть связаны функциональной зависи- мостью Y = j(X), когда одному значению X соответствует одно значение Y. В таком случае знание значения X позволяет вычислить соответствующее значение Y точно.

113

Но между СВ может существовать связь и другого рода, когда по изменению значений одной из них можно попытаться установить лишь приближенно закон распределения значений другой.

16.1. Пример. Пусть Y − урожай зерна, X − количество удобрений.

Пусть Ω − множество участков земли, на которых определены СВ X и Y.

Тогда если w − конкретный участок из Ω, то X(w) − масса внесенных на не-

го удобрений, Y(w) − урожай на нем некоторой с/х культуры. Ясно, что с увеличением (до известных пределов) X(w) увеличивается и Y(w). Но точ- но предсказать урожайность нельзя, так как на нее влияют и другие факто- ры (осадки, температура, состав почвы и т.д.). Поэтому на различных участках земли урожайность будет различной. Таким образом, если |Ω| = n, то каждому значению X = x соответствует некоторое множество {Y(w1),…,Y (wn)} значений (распределение) СВ Y. Весь урожай Y = Y(w1) + +… + Y (wn) при условии, что было внесено X = x единиц удобрения, оче- видно, зависит от x. Это дает нам пример статистической зависимости между X и Y.

Строгое определение статистической зависимости может быть сформулировано следующим образом.

16.2. Определение. Статистической зависимостью между компонен- тами СВ (X, Y) называется закон, который каждому наблюдавшемуся зна- чению x СВ X ставит в соответствие условное распределение наблюдав- шихся значений СВ Y.

Наиболее важной статистической связью является зависимость меж- ду значениями СВ Х и условным математическим ожиданием M(Y/X = x) СВ Y (определение 10.3)

M (Y / X = x) =

(x).

(16.1)

Уравнение (16.1) называется уравнением регрессии Y на X. График

функции y(x) называется линией регрессии Y на X.

Аналогично определяется регрессия X на Y

M ( X /Y = y) =

( y).

(16.2)

114

Пусть исследуется связь между СВ X и Y – компонентами СВ (X, Y). Пусть каждому значению Х соответствует несколько значений Y:

X = x; Y = y1, ..., Y = ym .			(16.3)
Тогда среднее арифметическое
		m
	y	x = (1/ m) × ∑ y j	(16.4)
		j =1

называется условным средним СВ Y относительно X = x.

Аналогично определяется условное среднее СВ X относительно Y = y:

		n
	x	y = (1/ n) × ∑ xi ,	(16.5)
		j =1
где
при Y = y X = x1,..., X = xn .			(16.6)

Из пп. 12.12, 12.14, 12.16 известно, что несмещенной, эффективной и состоятельной оценкой для МО является выборочная средняя. Поэтому

регрессионные зависимости (16.1) и (16.2) на практике заменяются корре- ляционными зависимостями (эмпирическими уравнениями регрессии):


	y		x = f (x)	(16.7)
и
		y = j( y).		(16.8)
	x	y = j( y).		(16.8)

Формулы (10.12), (10.13), (10.9) и (10.10) показывают, что восполь-

зоваться уравнениями (16.1) и (16.2) можно, если знать f(x, y). На практике f(x, y), как правило, неизвестна. В распоряжении имеются только наблю- давшиеся значения СВ (X, Y)

(x1, y1), ..., (xn, yn) .

(16.9)

Если результаты наблюдений (16.9) изобразить в виде точек на плоскости в декартовой системе координат, то получим точечную диа- грамму, называемую корреляционным полем (рис. 16.1).

115

∙	∙∙	∙
∙∙	∙	∙∙
∙	∙	∙
∙	∙	∙
∙∙	∙	∙∙
∙∙	∙	∙∙	x
∙	∙	∙	x

Рис. 16.1

На основании анализа корреляционного поля делаем вывод, что эм-

пирическая линия регрессии (график (16.7) или (16.8) должна проходить через точки (16.9) таким образом, чтобы усреднить результаты измерений (16.9). Усреднить здесь означает найти такой вид функции (16.7)

x = f (x, a, b,¼, c),

(16.10)

график которой наилучшим образом (в смысле метода наименьших квад- ратов) приближался бы к неизвестной линии регрессии (16.1).

Параметры (a, b,..., c) функции (16.10) находятся по методу наи- меньших квадратов (МНК), при котором требуется, чтобы выполнялось условие

n					(x ))2
S = ∑	( y	-	y	x	(x ))2	= min,	(16.11)
i=1	i			x	i
i=1

где yi взяты из (16.9), а y x (xi ) вычислены по формуле (16.10).

Первая задача теории корреляции – установить вид функций (16.1), (16.2) или (16.7), (16.8) (т.е. являются они линейными, квадратичными, по- казательными и т.д.).

Вторая задача теории корреляции – оценить силу (тесноту) связи между X и Y.

Как отмечено в замечании 10.10, мерой тесноты связи может слу- жить оценка коэффициента корреляции ρXY .

Если обе функции (16.7) и (16.8) являются линейными, то и корреля- ционная зависимость между X и Y называется линейной.

116

Рассмотрим метод расчета эмпирических линейных уравнений рег- рессии с помощью МНК по несгруппированным данным (16.9).

Итак, пусть (16.10) имеет вид

x = a + b x .

(16.12)

Тогда условие (16.11) запишется так:

n	- a - bx )2	= min .
S = S (a, b) = ∑( y	- a - bx )2	= min .	(16.13)
i	i

i=1

Поиск минимума функции S(a, b) осуществляется в стационарной

точке

( y

- a - b x ) × (-x ) = 0

= 2∑

b∑x2

+ a∑x

∑x y

i=1

i i

i=1

= 2∑

( y - a - b x ) × (-1) = 0

b∑x + a × n = ∑ y

i=1

i =1

Решая систему (16.14) по правилу Крамера, получаем

a =

∑x2

× ∑ y - ∑x ×

∑x y

i i

n∑x2 - (∑x )2

n∑xi yi - ∑xi ∑ yi

b =

n∑xi - (∑xi )

(16.14)

(16.15)

где все суммирования производятся от i = 1 до n.

Если требуется по данным (16.9) получить линейное уравнение рег- рессии X на Y, то аналогичные рассуждения дают нам, что в уравнении

y = a '+ b 'y

(16.16)

a′ и b′ вычисляются по формулам

117

a '=	∑ y2	× ∑x - ∑ y × ∑x y
a '=	i	i		i		i i ,
	n∑ y2		- (∑ y )2
		i		i


	n∑xi yi - ∑ yi ∑xi
b '=	n∑xi yi - ∑ yi ∑xi				,
b '=					,
		2		2
	n∑ yi - (∑ yi )

где также все суммирования производятся от i = 1 до n. На практике для нахождения уравнений y = a + b x

ставляется следующая таблица:

(16.17)

и x = a '+ b 'y со-

xi	yi	xi2	yi2	xi yi
x1	y1	x12	y12	x1 y1
M	M	M	M	M	(16.18)
xn	yn	xn2	yn2	xn yn
xn	yn	xn2	yn2	xn yn

n	n	n	n	n
∑xi	∑ yi	∑xi2	∑ yi2	∑xi yi
i =1	i =1	i=1	i =1	i=1

В последней строке таблицы (16.18) имеются все данные для вычис- лений по формулам (16.15) и (16.17).

16.3. Определение. Пусть имеется выборка (16.9) объема n. Тогда выборочной ковариацией выборки (16.9) называется число

K XY = S

∑

- x)( y - y),

(16.19)

n i=1

где x и y – средние выборочные первых и вторых координат точек из

(16.9) соответственно.

Если ввести обозначение

∑x y

= xy,

(16.20)

i i

n i=1

то

XY =

( ∑x y -

∑ y -

∑x + n

) =

i i

∑x

∑ y -

∑ y

∑x +

× n ×

∑x ×

∑ y =

x y

n n

118

Итак,

XY =

x y

(16.21)

16.4. Определение. Пусть имеется выборка (16.9). Тогда ее выбо-

рочным коэффициентом корреляции называется число

r =	K XY		,	(16.22)

XY	SX	× SY

гдеSX2 и SY2 - выборочные дисперсии для первых и вторых координат то-

чек из (16.9) соответственно. Как показано в лемме 12.4,

S	2	= x2 - (	x	)2	и S2	= y2 - (	y	)2.	(16.23)
	X				Y

Разделив обе части уравнения (16.14) на n, получаем (в обозначениях из (16.19) и (16.20):

×b + x × a = xy

по правилу Крамера

×b +

a =

× x

2 -

a =

= (16.23) =

SX2

x2 - (

× (x2

- (

)2 ) -

× (

)

= (16.23), (16.21) =

SX2

× SX2

K XY

= y - x ×

;

SX2

b =

119

Подставив вычисленные значения a и b в уравнение регрессии

(16.12), получим:

x =

K XY

× x ,

SX2

или, ввиду (16.22),

K XY

(x -

) =

rXY SX SY

(x -

) = r

(x -

SX2

XY SX

Итак, уравнение прямой регрессии Y на X имеет вид:

= r

(x -

(16.24)

XY SX

Аналогично, уравнение прямой регрессии X на Y имеет вид:

= r

( y -

(16.25)

x y

Из уравнений видно, что обе прямые (16.24) и (16.25) проходят через точку (x, y) и совпадают, когда |rXY| = 1. Это указывает на сильную связь признаков X и Y.

Если в уравнениях (16.24) и (16.25) коэффициенты линейной регрес-

сии Y на X и X на Y соответственно

b = r

b' = r

(16.26)

XY S

положительны (отрицательны), то СВ X и Y одновременно возрастают

(убывают).

Степень связи зависит от угла Q между прямыми (16.24) и (16.25)

(рис. 16.2).

′

y¢

x y

= b x + a

= bx + a

x′

С(

)

Рис. 16.2

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2412 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб48умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб39умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб37умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб43умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб44умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб50умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб42умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб90умк_Яско_ Диф.уравнения_Ряды.pdf