
14-es_1 / Высшая математика (РТФ) / умк_Пальчик_Теория вероятностей
.pdf
|
|
|
|
|
|
|
|
|
1 |
|
x'' |
− |
z2 |
'' |
|
|
|
' |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Pn |
(k1, k2 ) » |
|
|
|
|
|
∫ e |
|
2 |
dz = F(x ) - F(x ), |
(5.20) |
||||||||||
|
|
|
|
|
|
||||||||||||||||||||
2p |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
' |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где x' = |
k1 |
− n p |
, |
x ''= |
k2 |
− n p |
. |
Æ. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
n p q |
|
|
n p q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
z2 |
|
||
5.14. Замечание. Для функции F(x) = |
|
1 |
|
∫ e− |
|
|
|||||||||||||||||||
|
|
2 dz имеются специ- |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
2p |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||
альные таблицы значений для |
аргументов |
x |
Î [0; |
5]. Кроме того, |
|||||||||||||||||||||
F(– x ) = – F(x). Для х > 5 F(x) =1/2.
j(x) и F(x) называются функциями Лапласа.
5.15. Пример. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что из 400 выбранных деталей окажется от 70 до 100 деталей, не прошедших проверку ОТК.
О. P400(70; 100) ≈ F(x²) – F(x¢), |
|
|
|
|
||||
где x' = |
70 - 400 × 0, 2 |
|
= -1,25; |
x'' = |
100 - 400 × 0, 2 |
= 2,5. |
||
|
|
|
|
|||||
400 × 0, 2 × 0,8 |
|
|
20 × 0,4 |
|
||||
F(x²)= F(2,5) = 0,4938; F(x¢) = F(– 1,25) = – |
F(1,25) = – 0,3944. |
|||||||
P400(70; 100) » 0,4938 – (– 0,3944) = 0,8882. |
Ä. |
|
||||||
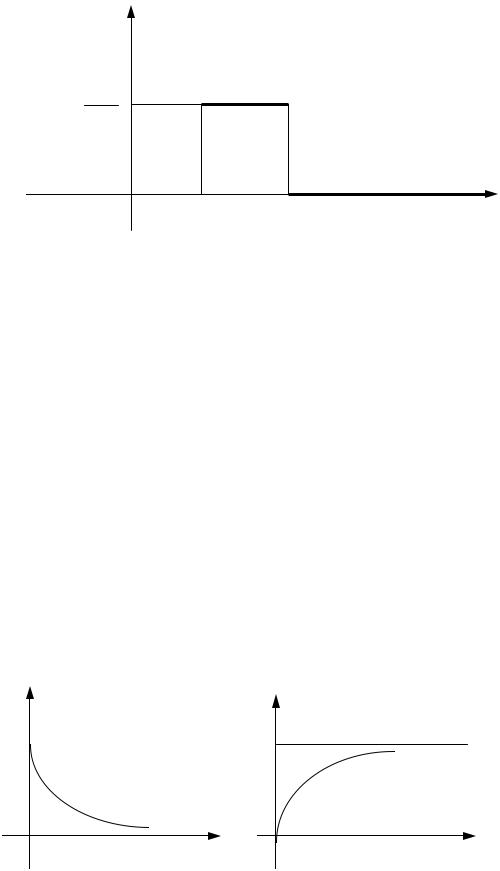
5.16. Определение. СВ X называется равномерно распределенной на интервале [a, b], если она принимает все значения этого интервала с оди- наковой вероятностью c, а вне этого интервала не принимает значений, т.е.
|
|
c, |
a £ x £ b |
|
|
|
f (x) = |
(5.21) |
|
|
|
0, |
x < a, x > b. |
|
Так как |
|
|
||
|
|
∞ |
b |
|
|
|
1 = ∫ f (x) dx = 0 + ∫c × dx - 0 = c(b - a), |
||
|
|
−∞ |
a |
|
то f (x) = c = |
1 |
, и график f(x) имеет вид, представленный на рис. 5.1. |
||
b - a |
||||
|
|
|
||
41
f(x)
1
b - a
|
|
|
|
|
|
|
|
|
x |
|
|
|
0 |
a |
|
b |
|
|
|
||
|
|
|
|
Рис. 5.1 |
|
|
|
|
||
5.17. Определение. Показательным (или экспоненциальным) зако- |
||||||||||
ном распределения СВ X называется закон вида |
|
|
|
|||||||
|
|
|
0, |
при |
x < 0 |
|||||
|
|
|
|
|
|
|
(5.22) |
|||
|
|
f (x) = |
|
|
|
|
||||
|
|
le-λx , |
при |
x ³ |
0, |
|
|
|||
где λ = const, λ > 0. |
|
|
|
|
|
|
|
|
||
|
x |
0 |
|
x |
|
x |
|
1 |
|
|
F (x) = ∫ f (x)dx = ∫ 0 × dx + ∫le−λxdx = l∫e−λx (- |
)dx(-lx) = |
|||||||||
|
||||||||||
|
−∞ |
−∞ |
0 |
|
0 |
|
l |
|||
= e−λx | 0x=1 - e−λx.
Графики f(x) и F(x) имеют вид, представленный на рис. 5.2.
f (x) |
F(x) |
l |
1 |
x |
x |
Рис. 5.2
42
6. Функция одномерной СВ Х + У, X × Y. Числовые характеристики одномерной СВ (МО, дисперсия, моменты распределения). Свойства МО и дисперсии (D)
6.1.Определение. Пусть задана функция от одной переменной
y = f(x) |
(6.1) |
с областью определения D*. Предположим, что все значения некоторой СВ X принадлежат множеству D*. Если СВ X приняла значение x D*, то условимся говорить, что равенство (6.1) определяет новую СВ Y, и писать
Y = f(X), |
(6.2) |
причем считается, что с какой вероятностью СВ X приняла значение x, то с такой же вероятностью СВ Y приняла значение y, определяемое законом (6.1). Эту новую СВ Y называют функцией СВ X.
По аналогии с моделью (ΩX , FX, PX ) может быть построена и модель
(ΩY , FY, PY ), где FY |
– |
σ-алгебра для ΩY, а вероятность любого события |
|||
B FY высчитывается по тому же принципу (4.1), которым мы пользова- |
|||||
лись при построении модели (ΩX , FX, PX ) в лекции 4: |
|
||||
P (B F ) = P ( f |
−1(B) F |
) = P( X −1( f −1(B)) F ), |
(6.3) |
||
Y |
Y |
X |
X |
|
|
при этом f −1(B) является прообразом B в FX , т.е. |
|
||||
|
|
f −1(B) = {x F | f (x ) B}. |
|
||
|
|
|
i X |
i |
|
В связи с (6.2) возникает вопрос: если закон распределения СВ X из- вестен (f(x), или F(x)), то как найти закон распределения СВ Y из (6.2)?
Начнем с определения функции распределения G(y) = P(Y < y) СВ Y, если известна зависимость (6.2) и известна плотность распределения p(x) СВ Х.
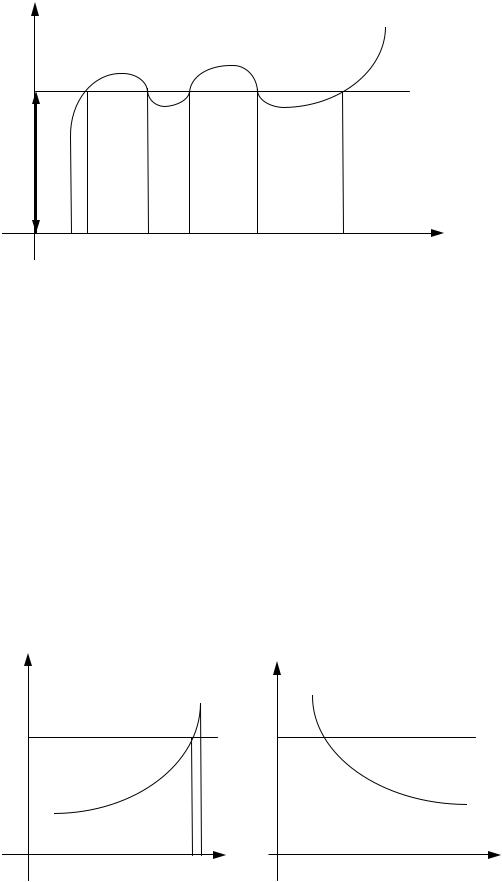
Пусть зависимость (6.2) изображается графиком на рис. 6.1.
43
y
y=f (x)
y |
|
|
|
|
|
a |
|
|
|
b |
x |
c1 d1 |
c2 |
d2 |
c3 |
dn |
|
Рис. 6.1
Проведем на расстоянии y прямую, параллельную оси Ox. Выделим те участки [ci, di] кривой, на которых Y < y. Тогда событие (Y < y) равно- сильно попаданию значений СВ X на один из интервалов [ci, di]. По аксио- ме ЗК имеем:
k |
di |
G( y) = P(Y < y) = P(( X ]c1, d1[ X ]c2 , d2[ K) = ∑ |
∫ p(x) dx, (6.4) |
i=1 c |
|
|
i |
где k – число подходящих интервалов. |
|
Далее, плотность распределения g(y) СВ Y из (6.2) определяется как |
|
обычно: |
|
g(y) = G′(y). |
(6.5) |
Рассмотрим частный случай (6.2).
Пусть y = f(x) монотонна на ]a, b[ и, в частности, имеет обратную функцию x = f -1(y) (рис. 6.2).
y |
y |
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
||
a |
xb |
a x |
b |
||||
|
|
a) |
|
|
|
б) |
|
Рис. 6.2
44

Для случая на рис. 6.2, а имеем:
x |
f −1 ( y) |
|
G(y) = P(Y < y) = P(a < X < x) = ∫ p(x) dx = |
∫ |
p(x) dx. |
a |
a |
|
Дифференцируем обе части этого равенства по переменному верх- |
||
нему пределу. Согласно теореме Барроу, получаем |
|
|
g( y) = G'( y) = p( f − 1( y)) × ( f − 1( y)) '. |
(6.6) |
|
Если же имеем случай убывания (рис. 6.2, б), то
g( y) = G'( y) = - p( f − 1( y)) × ( f − 1( y))
или, объединив эти формулы, имеем:
g( y) = p( f −1( y)) × (| f −1( y)|)', |
(6.7) |
т.к. при убывающей функции f −1 ее производная отрицательна.
6.2.Пример. Пусть СВ X имеет плотность распределения
p(x) = |
1 |
|
e−( x−m) |
2 |
/ 2σ |
2 |
|
|
|
|
|
, |
|||
|
|
|
|
|
|||
s 2p |
|
|
|||||
|
|
|
|
|
|
||
а
Y = aX + b.
Найти g(y).
О. Функция (6.9) монотонна, имеет обратную
X = Y − b . a
По формуле (6.7) имеем:
1 |
|
|
|
−( |
y−b |
−m)2 / 2σ2 |
1 |
|
|
1 |
|
|
|
−( y −(am+b))2 / 2a2σ2 |
|
|
|
|
a |
|
|
|
|
|
|||||||
g( y) = |
|
|
|
× e |
|
|
× |
|
|
= |
|
|
|
× e |
. |
s × |
|
|
|
|
| a | |
| a | s |
|
|
|||||||
2p |
|
|
2p |
||||||||||||
(6.8)
(6.9)
(6.10)
(6.11)
То есть g(y) имеет тот же вид, что и (6.8), но с параметрами |a| s вме- сто s, и am + b вместо m. Ä.
45
Пусть теперь X и Y – независимые ДСВ, имеющие законы распреде-
ления
P( X = xi ) = pi , |
i = |
1, m |
; |
(6.12) |
||
P(Y = y j ) = p% j , |
j = |
|
. |
(6.13) |
||
1, n |
||||||
Рассмотрим две новые СВ: |
|
|
|
|
|
|
X + Y и X × Y. |
(6.14) |
|||||
Выясним законы распределения этих двух СВ сначала на примерах,
азатем обобщим их в виде правил.
6.3.Пример. Даны законы распределения для независимых X и Y.
X |
2 |
–1 |
0 |
|
Y |
0 |
1 |
2 |
P |
0,3 |
0,2 |
0,5 |
|
p% |
0,4 |
0,5 |
0,1 |
|
|
|
|
|
|
|
|
|
Найти законы распределения СВ X + Y и X × Y.
О. СВ X + Y принимает возможные значения (xi + yj) {-2; -1; 0; 1; 2}.
При этом событие (X + Y = – 2) = (X = – 2) и (Y = 0) = ( X = -2) Ç (Y = 0).
Аналогично,
(X + Y = – 1) = (X = – 2) и (Y = 1) или (X = – 1) и (Y = 0) =
= [( X = -2) Ç (Y =1)] È[( X = -1) Ç (Y = 0)].
(X +Y = 0) =[(X = -2) Ç(Y = 2) È[(X = -1) Ç(Y =1)] È[(X = 0) Ç(Y = 0)] . ( X + Y =1) = [( X = 0) Ç (Y =1)] È[( X = -1) Ç (Y = 2)] .
( X + Y = 2) = ( X = 0) Ç (Y = 2).
Так как СВ X и Y независимы по условию, то P[( X = xi ) × (Y = y j )] = = pi × p% j . Поэтому
P( X + Y = -2) = P( X = -2) × P(Y = 0) = 0,3 × 0,4 = 0,12 .
P( X + Y = -1) = 0,3 × 0,5 + 0, 2 × 0, 4 = 0,23.
P( X + Y = 0) = 0,3 × 0,1 + 0,2 × 0,5 + 0,5 × 0, 4 = 0,33.
P( X + Y =1) = 0,5 × 0,5 + 0, 2 × 0,1 = 0,27 .
P( X + Y = 2) = 0,5 × 0,1 = 0,05.
46
Итак,
|
X + Y |
|
–2 |
–1 |
|
0 |
|
1 |
2 |
|
|
P |
|
0,12 |
0,23 |
|
0,33 |
|
0,27 |
0,05 |
∑ pi =1 |
Далее, СВ XY принимает значения (xi |
× y j ) Î{-4, - 2, -1, 0}. |
|||||||||
( XY = -4) = ( X = -2) Ç (Y = 2) . |
|
|
|
|
|
|||||
( XY = -2) |
= [( X = -1) Ç (Y = 2)] È[( X = -2) Ç (Y =1)]. |
|
||||||||
( XY = -1) = ( X = -1) Ç (Y =1) .
( XY = 0) = [( X = -2) Ç (Y = 0)] È[( X = -1) Ç (Y = 0)] È
È[( X = 0) Ç (Y = 0)] È[( X = 0) Ç (Y =1)] È[( X = 0) Ç (Y = 2)].
Сводим к вероятностям
P( XY = -4) = 0,3 × 0,1 = 0,03.
P( XY = -2) = 0,3 × 0,5 + 0, 2 × 0,1 = 0,17 .
P( XY = -1) = 0,2 × 0,5 = 0,10 .
P( XY = 0) = 0,3 × 0, 4 + 0,2 × 0, 4 + 0,5 × 0,4 + 0,5 × 0,5 + 0,5 × 0,1 = 0,7.
Итак,
XY |
–4 |
–2 |
–1 |
0 |
|
P |
0,03 |
0,17 |
0,10 |
0,70 |
Ä. |
|
|
|
|
|
|
После этого примера становится понятным следующее
6.4. Определение. Суммой X + Y двух независимых СВ X и Y на- зывается СВ, возможные значения которой равны суммам каждого воз- можного значения X с каждым возможным значением Y, а вероятности возможных значений X + Y равны суммам произведений вероятностей подходящих значений каждой из них.
Произведением X ×Y двух независимых СВ X и Y называется СВ, возможные значения которой равны произведениям каждого возможного значения X на каждое возможное значение Y, а вероятности этих значений равны суммам произведений вероятностей подходящих значений каждой из них.
47

В частности, полагая X = C = const, получаем, что СВ CY – это СВ, возможные значения которой равны Cyj, где yj – возможные значения Y, и
p(Cy j ) = p( y j ), j =1, m.
Иногда знать F(x) или f(x) необязательно или не удается. Тогда при- ходят на помощь так называемые числовые характеристики СВ.
6.5. Определение. Математическим ожиданием (кратко: МО) СВ X называется число M(X) (или mX), определяемое по формуле
|
|
n |
" ДСВ*)X, |
|
|
∑ p x |
|
||
|
|
i i |
|
|
|
|
i=1 |
. |
(6.15) |
mX = M( X ) = |
¥ |
|
||
|
∫ |
x f (x) dx |
" НСВ X |
|
-¥ |
|
|
|
|
*) Для ДСВ МО называется также «средним значением» ДСВ. Ясно, что
|
|
|
M(X) = const. |
|
(6.16) |
|
6.6. |
Теорема. Пусть X – произвольная СВ, Y = j(X) – |
новая СВ. |
||||
Тогда |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
∑j(xi ) pi |
" ДСВ Y , |
|
|
|
|
|
|
i=1 |
. |
(6.17) |
|
|
M (Y ) = M (j( X )) = |
¥ |
||||
|
|
|
∫ j(x) f (x) dx |
" НСВ Y |
|
|
|
|
-¥ |
|
|
|
|
О. Утверждение для ДСВ Y очевидно. Пусть Y – монотонная функ- |
||||||
ция. Тогда, по определению 6.5 |
|
|
|
|||
¥ |
|
|
y = j(x); x = j-1( y) |
|
|
|
|
|
|
|
|||
|
f ( y) = (6.6) = f (j-1( y)) × (j-1( y))' = f (x) × (j- 1( y) ') |
|
||||
M (Y ) = ∫ |
y × f ( y) dy = |
= |
||||
-¥ |
|
|
dy = j'(x) dx |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
¥
= ∫
-¥
j(x) × f (x) × (j-1( y))' × j'(x)
1442443
y'x ×xy' =1
¥
dx = ∫ j(x) × f (x) dx. Ä.
-¥
48
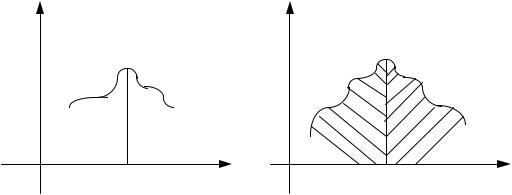
6.7.Определение. Модой ДСВ X называется ее наиболее вероят- ное значение. Модой НСВ X называется такое ее значение xмо, при котором плотность распределения имеет максимум (рис. 6.3.).
6.8.Определение. Медианой СВ X называют такое ее значение хме, относительно которого равновероятно получение большего или меньшего
значения СВ Х, т.е. Р1 = Р2, где Р1 = Р(Х < xме), Р2 = Р(Х > хме).
|
1 |
= |
xме |
|
2 |
= |
∞ |
|
|
|
|
|
|
∫ |
f (x) dx, |
∫ |
f (x) dx, то хме |
– |
это абсцисса точки, в |
||||
Так как |
P |
-∞ |
P |
|
|||||||
|
|
|
|
|
|
xме |
|
|
|
||
которой площадь |
|
фигуры, |
ограниченной кривой f(x), делится пополам |
||||||||
(рис. 6.4.). |
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
xмо |
xме |
Рис. 6.3 |
Рис. 6.4 |
6.9. Определение. Отклонением СВ X называется СВ X – M (X) (напомним, что по (6.16) M(X) = const; см. 6.4.). Дисперсией СВ X называ- ется математическое ожидание квадрата отклонения СВ X:
σ2 |
= D( X ) = M [( X − M ( X ))2 ]. |
(6.18) |
||
X |
|
|
|
|
Из (6.18) и (6.15) получаем формулу для вычисления D(X): |
|
|||
|
|
n |
|
|
|
∑(xi − mX )2 pi |
ДСВ X |
|
|
|
|
i=1 |
. |
(6.19) |
D( X ) = |
∞ |
|
||
|
∫ (x − mX )2 f (x) dx |
НСВ X |
|
|
−∞ |
|
|
||
49

МО характеризует СВ в среднем, это ее центр распределения. Вторая особенность СВ – степень разброса ее значений по отношению к ее цен- тру. Дисперсия и является оценкой этого разброса.
6.10. Определение. Средним квадратическим отклонением (или стандартом) СВ X называется величина
|
σX = + |
D( X ) |
. |
|
(6.20) |
||||
6.11. Определение. Начальным моментом k-го порядка СВ X назы- |
|||||||||
вается МО СВ Xk: |
|
|
|
|
|
|
|
|
|
|
|
|
γ |
k |
= M ( X k ). |
|
(6.21) |
||
|
|
|
|
|
|
|
|
|
|
В частности, |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
ДСВ X |
|
|
|
|
∑xik pi |
|
||||||
|
γk = |
∞ |
i =1 |
|
. |
(6.22) |
|||
|
|
∫ |
xk f (x) dx |
НСВ X |
|
||||
|
−∞ |
|
|
|
|
|
|
||
6.12. Определение. Центральным моментом k-го порядка СВ X на- |
|||||||||
зывается МО величины (X – M (X))k: |
|
|
|
||||||
|
μk = M[(X – M (X))k]. |
(6.23) |
|||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
∑(xi − mX )k pi |
|
ДСВ X |
|
||||||
μk = |
∞ i=1 |
|
|
|
|
|
|
. |
(6.24) |
|
∫ (x − mX )k f (x) dx |
|
НСВ X |
|
|||||
−∞ |
|
|
|
|
|
|
|
|
|
6.13. Свойства МО.
6.13.1. Если C – не СВ, то M(C) = C.
O. Не СВ принимает постоянное значение C. Ее можно рассматри- вать как ДСВ, принимающую значение X = C с вероятностью 100 %. По определению 6.5 тогда M (C) = C ×1 = C. Ä.
6.13.2. Если C = const, X – СВ, то M(CX) = C× M(X).
50
