2683

Если какое-либо из осевых отрезков является отрицательным, то над соответствующим символом в обозначении грани ста-

вится черточка. Например, если OB 3b (n 3), то обозна-

чение грани имеет вид (326).

Общие правила определения кристаллографических индексов таковы:

1)Находят отрезки, отсекаемые данной гранью на координатных осях, и определяют их в соответствующих осевых единицах m,n, p ;

2)Устанавливают величины, обратные найденным отрез-

кам;

3)Приводят полученные числа к наименьшим целым

числам.

Найденные при этом три взаимно простые целые числа (hkl) , будут кристаллографическими индексами грани.

Если рассматриваемая грань параллельна одной из осей,

сталлографические индексы этой грани запишутся (0kl). Если грань параллельна двух осям, то ее индексы (h00), (0k0) или (00l). В кубической сингонии, это будут грани куба (100), (010) или (001). Плоскость (111) в кубическом кристалле называется плоскостью октаэдра, плоскость (110) – плоскостью ромбического додекаэдра.

Для определения плоскостей кристалла в гексагональной системе пользуются четырьмя индексами (hkil), где i=-(h+k).

Кристаллографическое направление определяют нормалью к соответствующей плоскости (hkl) и символически записывают в виде hkl . Направляющие косинусы нормали вычис-

221

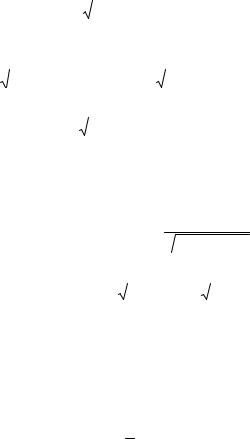
ляются через межплоскостное расстояние d, индексы плоскости (hkl) и осевые отрезки а, b, c.

Межплоскостное расстояние d определяется расстоянием первой из серии плоскостей от начала координат. Для кубической сингонии (а= b= c)

Теперь решим задачу: определить межплоскостные расстояния d100 , d110 и d111 для кубической решетки: простой (а), ОЦК (б), ГЦК (в).

a

а) Воспользуемся формулой dhkl , а – по- h2 k2 l2

нат, параллельной (100) является плоскость с m a/2, n ,

Из серии плоскостей, параллельных (110), первой от начала координат является эта плоскость, т.е. плоскость (110). Следовательно d110 a cos x a/3 .

Плоскость (111) проходит через узловую точку в центре кубической ячейки, при этом

222

Из системы плоскостей, параллельной плоскости (111), ближайшей к началу О является плоскость (111), для которой

Примечание. Начальная точка О является одной из узловых точек решетки.

6.251. Пусть некоторая плоскость на осях xyz прямо-

Оно называется уравнением плоскости в отрезках. Допустим, что точка К есть основание перпендикуляра, опущенного из начальной точки О на плоскость (1), а d – длина пер-

пендикуляра OK . Если при этом , , - направляющие углы

Уравнение (2) называется нормальным уравнением плоскости.

Теперь рассмотрим элементарную ячейку кубической решетки с параметром «а» и кристаллографическую плоскость, отсекающую на осях х, y, z отрезки 1 ma , 2 na,

3 pa, где m,n, p - целые числа. Уравнением этой плоскости будет равенство

Далее перейдем к индексам Миллера: h:k :l 1 : 1 : 1 . m n p

Уравнение плоскости получает вид

224

Поскольку рассматриваются одна и та же плоскость и один и тот же перпендикуляр из точки О на плоскость, то из сравнения (7) с (2) можно заключить, что

Итак, расстояние между плоскостями семейства (h,k,l,) для простой кубической решетки равно

В частности, когда m n p , то q m, h k l m и

d a/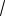3 .

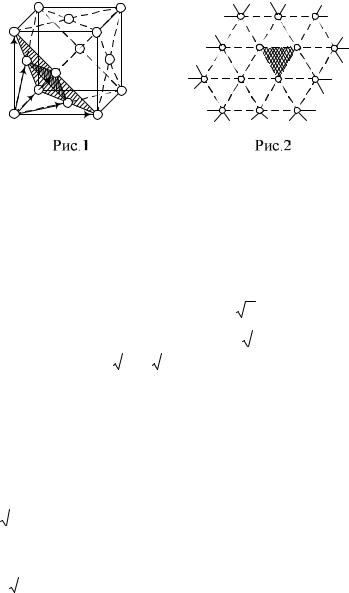
6.252. На рис.1 изображена ячейка ГЦК-структуры. Ближайшими атому О являются атомы 1,2 ,3 , расположенные в центрах смежных граней кубической ячейки. Плоскость, проходящая через узловые точки 1,2 ,3 , параллельна плоскости 1, 2, 3, отсекающей на осях x, y, z отрезки ma, na, pa, где m=n=p=1.

225

Следовательно, система плоскостей параллельных

1,2 ,3 , определяются единичной плоскостью с h k l 1,

т.е. плоскостью (111). Наиболее плотно упакованными плоскостями ОЦК-решетки являются плоскости (111).

Вычислим плотность атомов в этих плоскостях. Сетка узловых точек плоскости (111) состоит из треугольных ячеек

Каждый атом их трех расположенных в вершинах треугольника 1,2 ,3 (рис.2) принадлежит шести ячейкам. Поэто-

вательно плотность атомов в каждой из плоскостей (111) равна

226

6.253. В кристаллографии какое-либо направление в кристалле hkl определять нормалью к плоскости hkl . Для про-

стой кубической решетки (a b c) отрезки, отсекаемые на

d a/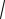h2 k2 l2 .

Косинусы направляющих углов для нормали к плоскости равны:

Отметим, что cos2 x +cos2 y +cos2 z =1.

6.254. Струна определенным образом натянута и закреплена на концах. При возбуждении поперечных колебаний на длине струны устанавливается система стоячих волн различных длин, удовлетворяющих условию:

Здесь n - длина бегущей n-й гармоники. Заметим, что точки закрепления струны являются узлами всех стоячих волн.

Учитывая, что n 2 , где - скорость волны, из (1) полу-

n

чим

Достаточно плотную совокупность частот n представим значениями непрерывной величины . Это позволяет для ин-

тервала частот от до d написать dn l d , что и

требовалось получить.

6.255. Решение данной задачи достаточно подробно изложено в «Ответах и решениях» сборника.

6.256. Воспользуемся формулой (6.7б)

2

dn 2 2 3 d ,

определяющей число нормальных колебаний (стоячих волн) на единицу объема трехмерного кристалла с частотами в интер-

вале от до d .

Число нормальных колебаний для объема V кристалла в том же интервале частот d будет равно

2

dN Vdn V 2 2 3 d .

6.257. Определим температуру Дебая для кристаллов:

228

а) однородного кристалла, состоящего из цепочки оди-

наковых атомов с n0 атомов на единицу длины.

Допустим, что концы цепочки закреплены, тогда уравнение n-й стоячей волны можно записать так:

(x,t) An sin(knx) sin nt .

Поскольку (x,t) периодическая,

kn n n,

a

где а – длина цепочки атомов; n =1, 2, …; - скорость всех волн (дисперсии нет). Полагая k, и n непрерывными величинами, на основании (2) будем иметь число нормальных ко-

Все атомы цепочки колеблются в одном направлении и, следовательно, имеют одну степень свободы (r=1).

Полное число стоячих волн в рассматриваемом кристалле равно

Здесь kБ - постоянная Больцмана.

б) Двумерного кристалла – плоской квадратной решетки

из одинаковых атомов содержащей п0 атомов на единицу площади.

Число нормальных колебаний на единицу площади

Поскольку атомы совершают колебания перпендикулярно плоскости кристалла, то реализуется одна колебательная степень свободы:

в) Простой кубической решетки из одинаковых атомов,

содержащей n0 атомов на единицу объемов.

230