Лекция №6 кривые линии. Поверхности и тела

Плоские и пространственные кривые.

Определение поверхностей тел.

Проецирование геометрических тел (призмы, пирамиды, цилиндра, конуса, шара, тора) на три плоскости проекций.

Подробный анализ проекций элементов геометрических тел (вершин, ребер, граней, осей и образующих).

Построение проекций точек, принадлежащих поверхностям.

Особые линии на поверхностях вращения: параллели, меридианы, экватор.

Образование наиболее часто встречающихся поверхностей.

6.1. Кривые линии

Кривой линией называется траектория точки, перемещающейся в пространстве по какому-либо закону. Однако, имеются кривые линии, не описываемые какой-либо закономерностью (незакономерные кривые линии). Кривая линия может быть также определена как однопараметрическое множество точек.

Плоской кривой линией называется линия, каждая точка которой принадлежит одной плоскости. В противном случае кривая линия называется пространственной (винтовая линия, линии пересечения двух поверхностей, из которых хотя бы одна является кривой поверхностью).

Если кривая образуется согласно какому-то закону и её образование может быть выражено математически, то такая кривая называется закономерной кривой. Закономерные линии описываются уравнениями и делятся на алгебраические второго и высшего порядков и трансцендентные, описываемые тригонометрическими функциями. Порядок кривой линии – это степень её уравнения или количество точек пересечения кривой линии с прямой линией (для плоских кривых) или количество точек пересечения с плоскостью (для пространственных линий).

Если образование кривой не может быть выражено математическим уравнением, то такая кривая называется незакономерной.

Циркульными линиями называются линии, построение которых можно осуществить циркулем (овал, овоид, завиток и др.).

Лекальными кривыми называются плоские закономерные линии, при вычерчивании которых используются лекала (эллипс, парабола, гипербола и др.). Циклические кривые линии – это линии, повторяющиеся в процессе образования (циклоида, эпициклоида, гипоциклоида и др.).

Аппроксимированные линии – это линии, приближенно замененные другими более удобными для вычерчивания линиями (например, эллипс иногда заменяют овалом).

Наиболее часто в технике применяются лекальные кривые линии, которые могут быть плоскими и пространственными. К ним относятся эллипс, парабола, гипербола, эвольвента, циклоида, винтовая линия и др.

Для построения проекций кривой линии следует найти проекции нескольких её точек и соединить их плавной кривой линией.

На рис. 6.1 представлены особые точки кривых линий. Особыми точками называются точки, в которых можно провести не одну, а две и более касательных или в которых изменяется направление движения точки или вращения касательной.

Точка перегиба – это точка, в которой кривая плавно переходит на другую сторону касательной (точка А) (рис. 6.1, а).

Узловая точка – это точка, в которой кривая линия сама себя пересекает (рис. 6.1, б) (точка В).

Точка возврата – это точка, в которой кривая имеет острие и в которой касательная является общей для обеих ветвей кривой (рис. 6.1, в) (точка С).

Точка повторения – это точка, в которой кривая касается самой себя (рис. 6.1, г) (точка D).

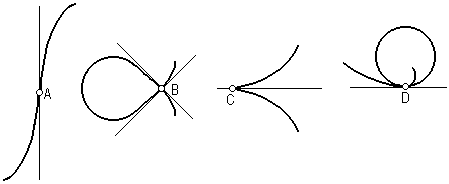
а) б) в) г)

Рис. 6.1. Особые точки кривых линий

Проекции кривой линии имеют следующие свойства:

1) В общем случае проекция кривой линии есть кривая линия;

2) Если точка принадлежит кривой линии, то её проекции принадлежат одноименным проекциям кривой;

3) Касательная к кривой линии проецируется в касательную к проекциям кривой линии.

Кривая линия называется пространственной, если она всеми своими точками не лежит в одной плоскости. К пространственным кривым линиям относятся цилиндрическая и коническая винтовые линии.

Цилиндрической винтовой линией называется траектория точки, движущейся по образующей прямого кругового цилиндра, которая, в свою очередь, вращается вокруг оси цилиндра. Расстояние, на которое перемещается точка по образующей за один полный её оборот, называется шагом винтовой линии. Ось цилиндра называется осью винтовой линии. Радиус основания цилиндра называется радиусом винтовой линии.

Рассмотрим построение цилиндрической винтовой линии, перпендикулярной к плоскости П₁ с шагом h и радиусом R. Такая винтовая линия на плоскости П₁ изобразится в виде окружности радиуса R.

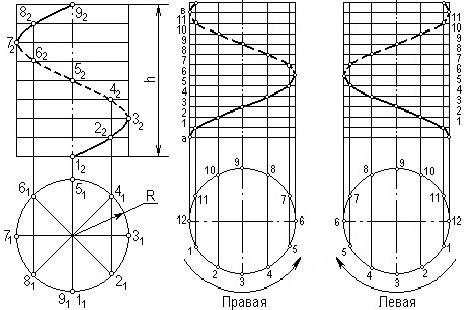
Чтобы построить фронтальную проекцию винтовой линии, следует разделить её горизонтальную проекцию на несколько равных частей. В данном случае разделим окружность на 8 частей. На такое же количество частей делим фронтальную проекцию. В данном случае высота фронтальной проекции является шагом винтовой линии. Построение винтовой линии на рис. 6.2, а начато с точки 1 (1₁,1₂).

При повороте точки на одну восьмую (1/8) часть дуги окружности она соответственно переместится по высоте вдоль оси винтовой линии на 1/8 часть шага (точки 2₁ и 2₂). При повороте точки на две восьмых дуги окружности точка переместится на две восьмых (2/8) высоты шага (точки 3₁ и 3₂) и т.д.

Соединив фронтальные проекции точек 1₂, 2₂, 3₂ и т.д. плавной кривой, получим фронтальную проекцию цилиндрической винтовой линии. Цилиндрическая поверхность при построении винтовой линии считается непрозрачной (рис. 6.2, а).

Различают правую и левую винтовую линии. Правой называют винтовую линию, когда точки при подъёме вращаются против часовой стрелки, а её участок на передней части цилиндра имеют подъём слева направо. У левой винтовой линии точка вращается по часовой стрелке, а подъём кривой линии на передней части цилиндра справа налево (рис. 5.6, б, в).

Конической винтовой линией называют траекторию точки, которая движется равномерно по образующей конуса вращения, а образующая совершает вращательное движение вокруг оси конуса с постоянной угловой скоростью.

Чтобы построить проекции конической винтовой линии, делим основание конуса на восемь равных частей. Отметим точки 1₀1₀', 2₀2₀' и т.д. Проводим через эти точки проекции образующих. На фронтальной проекции заданный шаг Н делим на то же количество частей. Через точки деления проводим горизонтальные прямые (рис. 6.3, а). Точки 1₂, 2₂, 3₂ и т.д. фронтальной проекции винтовой линии определяются в пересечении фронтальных проекций образующих конуса с соответствующими горизонтальными прямыми. Горизонтальная проекция конической винтовой линии строится по её фронтальной проекции. Последовательность построения показана на рис. 6.3, б. Горизонтальная проекция конической винтовой линии представляет собой спираль Архимеда.

а) б) в)

Рис. 6.2. Цилиндрическая винтовая линия

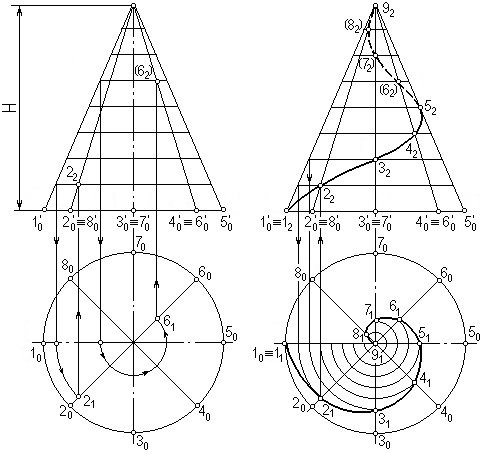
а) б)

Рис. 6.3. Коническая винтовая линия