3.3.2. Задачи на пересечение

Задача на пересечение двух прямых рассмотрена ранее в разделе "Пересекающиеся прямые".

Наиболее важной позиционной задачей является задача о пересечении прямой с плоскостью. При решении задачи могут встретиться следующие случаи пересечения:

1. Прямая общего положения пересекается с плоскостью частного положения.

2. Прямая частного положения (например, проецирующая) пересекается с плоскостью общего положения.

3. Прямая общего положения пересекается с плоскостью общего положения.

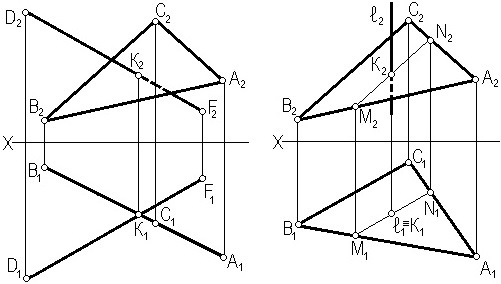
Решение первых двух задач не представляет особых трудностей (рис. 3.14). На рис. 3.14, а дано построение точки встречи прямой общего положения с горизонтально-проецирующей плоскостью, а на рис. 3.14, б – горизонтально-проецирующей прямой с плоскостью общего положения. Последняя задача решена с помощью вспомогательной прямой M-N.

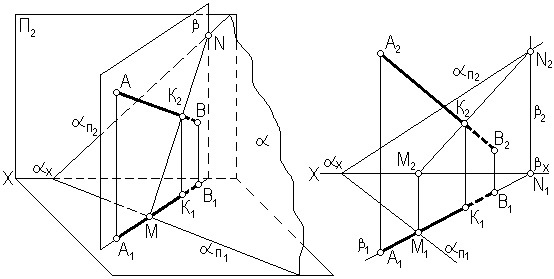
Для решения задачи о пересечении прямой с плоскостью в общем положении разработана следующая методика (рис. 3.15):

1) через прямую проводят вспомогательную плоскость частного положения β (чаще всего проецирующую плоскость, заданную следами);

2) находят линию пересечения заданной α и вспомогательной β плоскостей (линия M-N);

3) находят точку пересечения заданной прямой и найденной линии пересечения плоскостей. Полученная точка K искомая.

а) б)

Рис. 3.14. Пересечение прямой с плоскостью

На рис. 3.15, а дана пространственная схема решения задачи, в которой прямая пересекается с плоскостью, заданной следами. В качестве вспомогательной плоскости взята горизонтально-проецирующая плоскость β. На рис. 3.15, б в эпюрной форме показано решение этой задачи.

а) б)

Рис. 3.15. Пересечение прямой общего положения

с плоскостью общего положения

На рис. 3.16 дано решение задачи на пересечение прямой общего положения DF с плоскостью общего положения, заданной треугольником АВС. В качестве вспомогательной плоскости использована горизонтально-проецирующая плоскость α, проходящая через прямую DF. Эта плоскость пересекает плоскость треугольника по прямой МN. Фронтальная проекция М₂N₂ в пересечении с фронтальной проекцией прямой D₂F₂ определяет точку К₂. Точка К₂ является фронтальной проекцией точки пересечения прямой DF с плоскостью треугольника АВС. По фронтальной проекции точки К₂ определяем горизонтальную проекцию точки К₁. Точка К₁ лежит на линии связи, перпендикулярной оси Х в пересечении с D₁F₁. Видимость проекций определена методом конкурирующих точек (прямых).

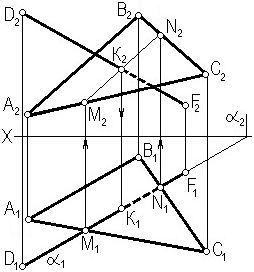
Рис. 3.16. Задача на пересечение прямой с плоскостью

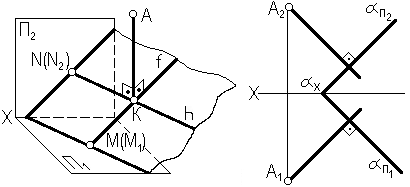
Частный случай пересечения прямой с плоскостью – прямая перпендикулярна плоскости. Из элементарной геометрии известно, что прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости (рис. 3.17, а). В качестве этих пересекающихся прямых наиболее целесообразно использовать горизонталь и фронталь плоскости. Это объясняется тем, что только в этом случае прямой угол будет проецироваться в натуральную величину на соответствующие плоскости проекций. Прямая будет перпендикулярна плоскости, заданной следами, если её проекции перпендикулярны соответствующим следам (рис. 3.17, б).

Если плоскость задана не следами, а каким-нибудь другим способом (двумя пересекающимися или двумя параллельными прямыми, треугольником и т.п.), то для построения прямой, перпендикулярной этой плоскости, следует построить в плоскости горизонталь и фронталь. В этом случае горизонтальная проекция перпендикуляра будет перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция перпендикуляра будет перпендикулярна фронтальной проекции фронтали, согласно правилу проецирования прямого угла (рис. 3.18). Точку пересечения перпендикуляра с плоскостью находим по ранее рассмотренной методике.

а) б)

Рис. 3.17. Перпендикуляр к плоскости

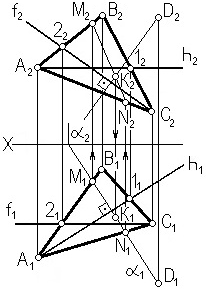
Рис. 3.18. Прямая перпендикулярная плоскости

Наиболее трудоемкой задачей является задача на пересечение двух плоскостей общего положения, заданных плоскими фигурами, например треугольниками, многоугольниками и т.д. При пересечении плоских фигур возможны два случая пересечения: полное пересечение и неполное пересечение.

В обоих случаях линия пересечения треугольников определяется двумя точками M и N (рис. 3.19), каждая из которых определяется как точка пересечения стороны одного треугольника с плоскостью другого. Отсюда следует вывод: для того чтобы построить линию пересечения треугольников, необходимо дважды решить задачу о пересечении стороны одного треугольника с плоскостью другого треугольника (типовая задача о пересечении прямой с плоскостью). При этом пару пересекающихся объектов можно подбирать произвольно. В любом случае линия пересечения будет построена.

Заключаем сторону ЕD во фронтально проецирующую плоскость β. Определяем линию пересечения 1-2 (1₂2₂ и 1₁2₁) заданной плоскости ΔАСВ со вспомогательной плоскостью β, и далее точку М. Затем, чтобы определить точку N, заключаем сторону ЕF треугольника DEF в горизонтально проецирующую плоскость α. Находим линию пересечения 3-4 этих двух плоскостей и далее точку N пересечения стороны EF с линией пересечения 3-4. Соединив эти точки, получаем линию пересечения этих двух треугольников.

С помощью конкурирующих точек 5, 6 определяем видимость одного треугольника относительно другого на плоскости П₂, а с помощью точек 3, 7 на плоскости П₁.

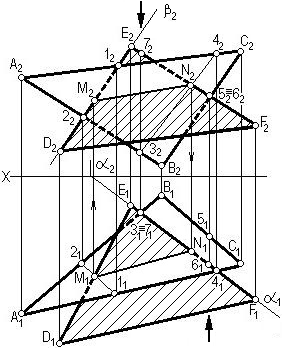
Рис. 3.19. Задача на пересечение плоскостей