§ 2. Два взаимодействующих ядра. Система ав

Гамильтониан системы двух спинов А и В, характеризующихся ре­зонансными частотами \>а и vb и константой спин-спинового взаимодействия /д«, имеет вид

Ж = '’д7_г (А) ; \’в/₂(В)-: ./авЫв- (2.23)

Проверим вначале, не являются ли мультипликативные функ­ции базиса собственными и для оператора Ж (2.23). Вычислим результат действия на функцию ф1 = аа:

МУх — Ж (аа) = -j- v_A (аа) ; -y-v_B(aa) ! -^-У_лв(аа). (2.24)

Таким образом, функция аа является собственной для оператора Ж с собственным значением, равны 1/2(уа+^в+^ав/2) .

Аналогично можно показать, что

Жч_а = #(ар)=(-у- у- ^-)ф₂ (2.25a)

#Ф₃ = Ж(ра)= (--T--I--T- Ь -^Фг-

(2.256)

Жщ = Ж (РР) = (—у 1Г ^ ^-Т^^-)ф⁴‘ (2.25в)

Отсюда следует, что функция ф₄=рр также-является собствен­ной функцией оператора Ж с собственным значением, равным (—v_a/2—vb/2—/дв/4). Что касается функций ф₂=ар и ф₃=ра, то они не являются собственными для оператора Ж■ Из формул (2.25а) и (2.256) следует, что действие оператора Ж на эти функ­ции приводит к смешиванию ф₂ и фз. Таким образом, две недостаю­щие собственные функции оператора Ж следует искать в виде линейных комбинаций функций базиса:

■фг—Яггфг+Ягзфз, (2.26а)

^з—Язгфг-Ь^ззфз. (2.266)

Уравнения (2.26) по существу представляют собой правила пе­рехода от одной ортогональной системы координат, связанной с функциями фг, фз, к другой ортогональной системе координат, свя­занной с собственными функциями оператора Ж■ Такое преобра­зование можно интерпретировать как поворот исходной системы координат на угол 0. Отсюда следует, что

г1>₂= (cos 0)ф₂+ (sin 0)фз, . (2.27а)

г1>з=— (sin 0)фг+ (cos 0)ф₃. (2.276) Рассмотрим действие оператора Ж на функцию г|}₂:

5&|>2 = (cos 0)#ф₂ I (311 :[0)$_Фз. (2.28).

Результаты действия оператора Ж на базисные функции фг и Фз запишем в виде

ЖЧг = Жг№%-гЖыЧъ> (2.29а)

#Фа=Я?з2«Р. ^-ЯГзаФз. (2.296)

где Жц— матричные элементы гамильтониана

Ж^ШЖШ- (2-30)

Подставив (2.29) в (2.28), получим

Ж^г = (cos 0)5^2292 ! (COS 0) <95?2зФз i (Sin 0) З^ззФз : (^П 0) ЖззФз-

(2.31)

Сгруппируем члены, содержащие функции фг и <f j:

5^фг = [(сое 0) 55?22 • i (sin 0) 55?зг] <Рг i ■ [(COS 0) S$?₃₂ i ■ (sltl 0) 55f₃₃] Фз

(2.32)

Используем то обстоятельство,'что функция г[5₂ является собст­венной функцией для оператора Ж • Поэтому

= ОДа =Ег (COS 0) ф₂ t £_г (sfri 0) ф₃. (2.33)

Приравнивая коэффициенты при функциях фг и фз в уравне­ниях (2.32) и (2.33), получим систему двух уравнений с двумя неизвестными £₂ и 0. Нетрудно убедиться в том, что

(2.34)

(2.35)

2Ж»

tg 20

22¹— Ж»

Е₂=*Жг2-\ (tg 9)5^23- Уравнения (2.34) и (2.35) фактически дают решение задачи. Мат­ричные элементы Шгъ и 3£₂з имеют вид

Ж₂₂ = (v//2 - v_B/2 - /лв/4), (2.36а)

Жзз = (—44/2 + v_B/2 - /лв/4), (2.366)

Ж_гз = Жг 2 = Jab/2, (2.36в)

Отсюда можно определить tg 2в, а следовательно, и угол 0:

(2.37)

2t%*23

• 0 =

  arctg

- <55? 3;

2 ^& Жщ-

На основании вычисленного угла 0 можно определить собствен­ное значение £2 по формуле (2.35).

Аналогичным образом следует искать и функцию 4>з- При этом получается тот же угол и еще одно значение энергии t_s:

£3 = %3'—(tg 6)5^23- (2.38)

Окончательно собственные функции и собственные значения гамильтониана (2.23) приведены в табл. 2.2.

Таблица 2.2

Собственные функции и собственные значения гамильтониана системы АВ

Уровень	Энергия	Собственная функция	Значение
1	«М.	аа	1
2	3%22 4" {tg0) i55?23	(cos0) (а[3) + (sin0) (^а)	0
3	<5^зз (tg0)i%’23	— (sin0) (аР) + (cos0) (Ра)	0
4	44	РР	—]

Для расчета интенсивностей переходов используем формулу

22. . В частности, для перехода 2->1 (рис. 2.3) имеем

12-^l = [ <1^11 J-\~ (²- (2.39)

Так как функция может быть записана в базисе функций ср₂ и фз,

то получим

/+1|;2 7^⁺(соз 0^₂+/+(sin 0)фз, . (2.40)

Поскольку

7+=7+(А)+7+(В),

то

/+ф² = /+(А)ф2 + /⁺(В)ф=СССС = ф_ь

/+фз=ф₁.

Отсюда следует, что

I₂^i = | (Фх | [(cos 0) } (sin 0)] ф_х) I² =

= (cos 0 i sin 0)²1 (ф_х j ф_х) |² = (1 ! sin 20). (2-41)

Рис. 2.3. Диаграмма энергети­ческих уровней систем IJ А В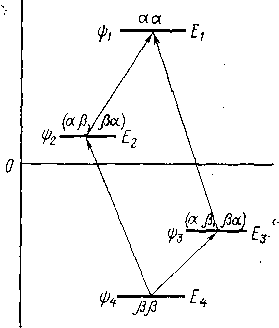

Аналогично вычисляются интенсивности остальных переходов (табл. 2.3). Таким образом, в-спектре системы АВ имеется, четыре линии с частотами v_b v~₂, v3, v₄ (рис. 2.4), симметрично располо-

Рис, 2,4. Типичный спектр ЯМР си­стемы АВ

женные относительно «центра тяжести спектра» при v₀~1/2(va+ +vb). Интенсивности внешних линий 1 и 4 всегда меньше интен­сивностей внутренних линий 2, 3 (это свойство спектров" сильно- связанных систем получило название «эффект крыш»). Расстояние между крайними линиями равно константе /дв-

Таблица 2.3

Частоты и интенсивности переходов в системе АВ

Переход	Частота перехода	Интенсивность перехода
2—>-1	11 — ^ 22 Ж 23^g0	1 + Sin2G
3—^1	&Сц + t55f»3tgt)	1—sin20
4 у 2	&£22 ^44 23^g$	1 + sin20
4—^3	^33 ^44 —■	1—sin2G

1. Анализ экспериментального спектра

Допустим, что нам известны частоты и интенсивности линий экспе­риментального спектра системы АВ. Требуется определить химиче­ские сдвиги и константу сиин-спинового взаимодействия.

Прежде всего следует определить положение «центра тяжести» спектра

vo=-1/2(vi+v₄) = 1/2(v2+v₄) (2.42)

Далее, используя параметры х и у (рис. 2.4)

x=vi—V4, (2.43)

y=v 2—V3, (2.44)

можно получить соотношения для искомых величин

Av = v_A—^k — Yxy, (2.45)

•^ав = 1/2 (х — у), (2.46)

откуда

6а = (v₀ !- -i-Avj/Vp, (2.47)

б_в = ^v₀ t-AvJ/v_p, (2.48)

где v_p — резонансная частота спектрометра (в Гц).

Кроме того, можно использовать соотношение для интенсив­ностей линий внешних и внутренних компонент спектра

1,/1₂=и/и=у/_х. (2.49)

Используя соотношение (2.49), можно провести анализ экспери­ментального спектра даже в том случае, если известны частоты и интенсивности только двух крайних линий (1,2 или 3,4).

2. Некоторые полезные следствия

Рассмотрим некоторые следствия из анализа АВ-систем, имеющие важное значение для понимания методов анализа спектров более сложных спиновых систем.

Слабосвязанные системы. Рассмотрим систему АВ при допол­нительном условии

Av=v_a—vb~>Jab- ■ (2.50)

Используя формулу (2.50), получим для матричных элементов га­мильтониана

S^n = v₀ i i/4,

Жш = Av —У/4,

Жаз = Av —J/4,

Жц = — v₀ 1- Jj4,

Ж 23 — Ж 32 = <7/2

(здесь и далее в § 2 индекс при константе опущен).

Подставляя приведенные выше значения матричных элементов в формулу (2.34), получим

Рис. 2.5. Типичный спектр ЯМР системы АХ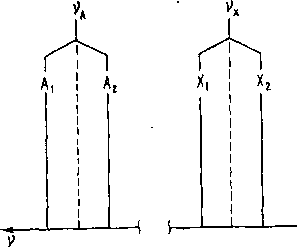

tg 20 =

2Av

откуда следует, что энергии стаци­онарных состояний будут с доста­точной точностью определяться диагональными матричными эле­ментами, т. е.

■Ei=vo-f-7/4,

£₂=Av-//4,

Еъ=—Av—//4,

£4 — —vo+^/4-

Таким образом, спектр двухспиновой системы, удовлетворяющей условию (2.50) (такая система называется слабосвязанной), со­стоит из двух дублетов, расположенных при значениях частоты ±Av± (1/2)7 и имеющих одинаковые интенсивности всех сигналов (рис. 2.5). В этом случае спин-спиновое взаимодействие можно считать слабым возмущением исходной системы уровней (при

7. = 0). Применяя теорию возмущений, можно показать в рамках первого порядка, что это приводит к появлению дублетных рас­щеплений для переходов, которые были вырождены в исходной системе. Для того чтобы-подчеркнуть слабую связь спинов, подоб­ное системы обозначают как АХ.

(2.51)

Сильносвязанные системы. Если параметры спиновой .системы удовлетворяют условию

Av=v_a—v_b</ab,

то такая система называется сильносвязанной. Для расчета спект­ров таких систем теория возмущений в принципе неприменима. Точные значения частот и интенсивностей линий могут быть полу­чены только в результате использования изложенного выше ме­тода.

Эквивалентные ядра. Рассмотрим случай, когда резонансные частоты ядер совпадают. Поскольку при этом Av=0, то согласно формулам (2.36) имеем для матричных элементов гамильтониана

Ж_п = v₀ — Jj 4,

Жъ = —Л±,

Ж33 — *^/4>

Ж и = — ^V0 -I *//4,

Ж ₂₃ = J/2.

Отсюда

tg 20 = ^22— _{= 00i}

22 — SK до

следовательно, 20 = 90°, 0=45°, tg0=l, sin 20=1. Пользуясь фор­мулами (2.35) и (2.38), получим для энергий состояний

£i=v₀+//4,

Ег= //4,

£з=- (3/4)7,

£4— —vo+^/4-

Нетрудно убедиться в том, что фактически спектр этой системы состоит из одной линии (двукратно вырожденной) с частотой vo. Два других Перехода "(3-*1 и 4->3) с частотами vo±/ имеют исчезающе малые интенсивности. Таким образом, несмотря на то, что между ядрами физически существует спин-спиновое взаимо­действие, оно не проявляется в спектре. Рассматриваемая система двух эквивалентных ядер обозначается как Ач.