Глава 2

МЕТОД СПИНОВОГО ГАМИЛЬТОНИАНА

Сложные органические соединения, содержащие большое коли­чество неэквивалентных протоков и ядер углерода, характеризуют­ся спектрами ЯМР, состоящими из десятков или даже сотен линий. Расчет этих спектров проводится с помощью метода квантовомеха- пического гамильтониана. В этой главе будут рассмотрены основ­ные положения этой теории и даны примеры расчета спектров простых систем.

§ 1. Основные понятия

1. Спин-гамильтониан

Б основе расчета стационарных состояний спиновых систем лежит уравнение Шредингера

(2.1)

где Ж — оператор Гамильтона; Ei — собственные значения этого оператора (энергии), отвечающие стационарным (разрешенным) состояниям системы г));. Таким образом, задача нахождения энер­гий системы сводится к решению уравнения (2.1), т. е. к поиску собственных функций и собственных значений гамильтониана.

В гамильтониане ЯМР высокого разрешения необходимо рас­смотреть два члена:

Ж = Жхс i Жкогя, (2.2)

где \Жхс — член, отвечающий экранированию ядер электронами (т. е. химическим сдвигам ядер); Жкссв — член, соответствующий косвенному спин-спиновому взаимодействию (гл. 1, § 6).

Химические сдвиги. Экранирование ядра электронами приводит к уменьшению магнитного поля на данном ядре на величину — сНо, где Но — внешнее магнитное поле; о — константа экранирова-

ния. Таким образом, зеемановская энергия г'-того спина с учетом экранирования будет определяться выражением

Для системы п ядер имеем

П

(2.3)

(2.4)

(2.5)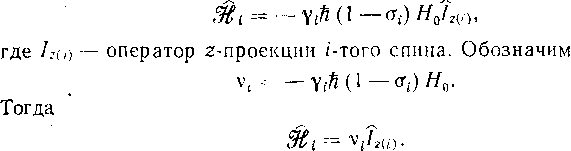

(2.6)

(2.7)

Константы спин-спинового взаимодействия. Для пары ядер А и В гамильтониан, соответствующий спин-спиновому взаимодейст­вию этих ядер, имеет вид (в единицах Й)

5^,= /abI.\Ib>

где 1_А и In — операторы спина ядер А и В. Для системы п спинов получим

(2.8)

i=\ /= 2

причем />/.

2. Спиновые функции и спиновые операторы

Используемые в гамильтониане (2.1) операторы /_г, 1;, I/ опреде­ляются правилами действия на спиновые функции. В квантовой механике спиновых систем для описания функций состояния при­влекается идея дискретности, экспериментальное обоснование ко­торой обсуждалось в гл. 1, § 2. Экспериментальные данные пока­зывают, что в магнитном поле изолированная частица со спином 1/2 может находиться в одном из двух разрешенных состояний и г))2, которым соответствуют. различные значения проекций маг­нитного момента на ось г, совпадающую с направлением внешнего _t магнитного поля. Для частицы с гиромагнитным отношением у

эти проекции равны — у% и j- yfi соответственно.

Функции t|?i и 'фг, для краткости обозначаемые а и (5, должны быть нормированы и ортогональны друг к другу. Эти требования записываются в виде соотношений

(2.9)

(2.10)

<а|а> — <Р|Р> — 1,

<а|р> — <р|а>=0.

Оператор' полного спина I определяется операторами-проекция­ми 1_Х, 1_У, Iz на оси координат. Операторы /_х, I_y, h задаются прави­лами действия на спиновые функции аир:

Т_га = — а, ?_гр = — -L р; (2.1 la)

Т_х7,р = (2-116)

V = -i-p, 7_уР = j-a. (2-11в)

Из формул (2.11) очевидно, что функции аир являются соб­ственными функциями оператора I_z с собственными значениями i/2 и —1/2 соответственно.

В случае п спиноз вводят понятие мультипликативных спиновых функций ф, представляющих собой произведения функций отдель­ных спинов ф,:

<р = ф1-ф2... фп. (2.12)

Так, для двухспиновых систем можно ввести четыре мульти­пликативные функции: ф1 = а1а₂; Ф₂ = а[Р₂; фз=р1а₂; ф4=Р)Рг (далее используется сокращенная запись, например ф2 = оф).

Очевидно, что для п спинов всего имеется 2^п мультипликатив­ных спиновых функции.

Свойства системы п спинов описывают с помощью оператора суммарного спина

! Т₂ I ... |-Т_л= 2 V (^2:13) ■

i=)

Оператор I определяется проекциями /_х, I_v, h на оси системы координат. Оператор 1_г, в частности, имеет вид

tl

Iz — Iz( 1) Ь 1г(2) 1 ••• \ ^г(п) — h(()- (2.14)

/=1

Нетрудно видеть, что мультипликативные функции (2.12) яв­ляются собственными функциями оператора 1_г с собственными зна­чениями

^/z==it^mh

/=1

где mi — значения z-проекций t-того спина. Так, в случае двух­спиновой системы мультипликативные функции аа, ар, Ра и рр характеризуются собственными значениями оператора 1_г, равными

1. 0, 0 и —1 соответственно.

Из формулы (2.15) следует, что z-проекция суммарного спина пробегает ряд значений от п/2 до —п/2 (через единицу), причем ¹ всего имеется п-(-1 значение проекции. Очевидно, что некоторые функции (2.12) имеют одинаковые z-прОекции. Такие функции на­зывают вырожденными по оператору 1_г. Так, для двухспиновой

Таблица 2.1

Треугольник Паскаля для системы п спинов (/= 1/2)

Значение 'г	-5/2 -2	-3/2	—1 —1/2 0 коэффициенты	1/2	1	.3/2	2 5/2
п — 0			1
1			1	1
2			1 2		1
3		1	3	3		1
4	1		4 6		4		1
5	1	5	10	10		5	1
системы	состояние	с 1г—	0 двукратно вырождено,			так	как ему

отвечают две функции оф и f5a. В общем случае кратность вырож­дения устанавливается с помощью треугольника Паскаля (табл. 2.1).

3. Частоты линий спектров невзаимодействующих спинов

Рассмотрим изолированное ядро со спином 1/2. В этом случае га­мильтониан имеет вид

ж = . (2.16)

Тгк как vi — постоянная величина, то оператор Гамильтона с точностью до постоянного множителя будет совпадать с операто­ром /_г. Следовательно,-собственные функции операторов 5? и/_г совпадают:

ffia = Vj/jCt = — v_ta, (2.17а)

£p = _Vir_zp = --L_Vj p. (2.176)

Таким образом, существует только два разрешенных состояния

изолированного спина'с энергиями —jvi и —образующих два

энергетических уровня на спиновой диаграмме (рис. 2.1). В этой системе возможен один переход с частотой

V = V_X '

(здесь и далее в этой главе предполагается, что энергия выра­жается в частотных единицах).

Рассмотрим теперь пару невзаимодействующих между собой спинов. Гамильтониан этой системы имеет вид

9S? = v₁/

(2.18)

2(1) 'I ^2/2(2)

где vi и V2 — частоты резонанса ядер.

Для того чтобы найти собственные функции, воспользуемся ба­зисом мультипликативных функций двухспиновых систем- Для на­чала проверим, не являются ли функции аа, ар, (За и РР собствен­ными функциями оператора Ж- Вычислим результаты действия Ж на эти функции:

Ж (аа) = _Vl-t-(аа) 1 v₂ -L (шх) = -у (v₂ ! v₂) (аа), (2.19a) Ж (ар) = Vi -L (ар) | v₂ —■ (ар) = ~ (^vi ^v2) (^аР)> (2.196) Ж(pa) = — v₁-i-(pa) i v₂i-(pa) = y-(—Vj • v₂) (pa), (2.19в)

Ж№) = - v_t -i- (PP) - v₂ -±- (PP) = (-_Vl - v₂) (PP). (2.19r

Ф

аа -ysrt,

ll h V,

/

V

/

-оф—^.Ег

\

л-

-V-

\

А

J8 ■

fifi Е4

)

-v,

Рис. 2.1. Диаграмма энергетических уровней изолированного спина (/=1/2)

Рис. 2.2. Диаграмма энергетиче­ских уровней двух невзаимодей­ствующих спинов (/=1/2) с раз­личными частотами резонанса vi и v₂

Таким образом, функции базиса являются собственными для оператора Гамильтона (2.18), причем собственные значения (т. е. энергии) этих функций различаются. Двухспиновая система (рис. 2.2) характеризуется четырьмя уровнями, между которыми

формально возможно шесть переходов. Энергии переходов опреде­ляются из соотношения

Vij = Ej—Ei, (2.20)

где предполагается, что j>i.

3. Интенсивности линий

Переходы между уровнями в ЯМР возбуждаются радиочастотным полем Н1, перпендикулярным к внешнему магнитному полю Н₀. Квантовомеханически это возмущение можно представить одним из операторов, перпендикулярных к l_z. Удобно, в частности, использо­вать оператор повышения 7+, определенный следующим способом:

Т+ = Т_Х i и_у. , (2.21)

Используя формулу (2.21), можно показать, что относительная ин­тенсивность линии, соответствующей переходу t->/, определяется формулой

1-ч = \Ш1⁺\Ъ)\*> ■ {2.22)

где г|з; и — собственные функции t-того и /-того состояний.

Для изолированного спина интенсивность единственного пере­хода согласно (2.22) будет равна единице. Для системы двух изо­лированных спинов, образующих систему четырех уровней, не­трудно убедиться в том, что интенсивности нуль-перехода (сф-э-ра) и двухквантового перехода (|5|3->~аа) равны нулю. Таким образом, из шести переходов, формально существующих в этой системе, фактически наблюдается четыре. Обратим внимание на то, что частоты переходов |3|3—>-(За и а(3—каа, а также частоты пере­ходов |3р->сф и |3а->аа попарно совпадают. Таким образом, спектр должен состоять из двух линий с частотами \ч и каждая из которых является двукратно вырожденной. Используя формулу

22. , можно показать, что относительные интенсивности каждого из четырех переходов равны единице.