§ 6. Взаимодействия ядерного магнитного момента

Прежде, чем приступить к анализу той информации, которая со­держится в сигнале ядерного магнитного резонанса, полезно систе­матически рассмотреть взаимодействия, в которых принимает участие ядерный магнитный момент. Энергия взаимодействия во всех случаях имеет классическую форму

Е=— ц-Н.

Таким образом, каждому взаимодействию можно поставить в соот­ветствие некоторое магнитное поле, а сам анализ взаимодействий сводится к рассмотрению магнитных полей, действующих на ядро. Для количественной оценки взаимодействий в нашем случае удобно использовать частотные единицы (Гц) (перевод в шкалу энергий проводится умножением на К).

Прямые диполь-дипольные взаимодействия. В конденсирован­ной фазе (жидкости, твердые тела) рядом с рассматриваемым ядерным моментом |х₂ может находиться другая магнитная частица (диполь) Hi (ядро или электрон) (рис. 1.17). Магнитная частица Ц] создает около себя магнитное поле, напряженность которого опре­деляется по формуле

Я = -^l-(3cbs² 0— 1), (1.40)

г³

где г — расстояние между моментами Hi и Ц2', 0 — угол, образован­ный направлением г ₁₂ и осью поляризующего поля (г). Анализ формулы (1.40) показывает, что локальное поле диполя быстро падает с увеличением расстояния, а также что поле равно нулю при угле 0=54°44' (этот угол называют «магическим»). Если p,i — протон, то при r= 1 А, 6 = 0°, величина напряженности локального поля достигает 1,4-Ю^-3 Т. Поскольку локальные поля на разных ядрах изучаемого кристалла (или поликристалла) могут принимать различные значения от —(х/г³ до +2|л/г³, то ширина резонансной области может достигать 100 кГц. В невязких жидкостях магнитные моменты быстро рео- риентируются друг относительно друга, что приводит к резкому сужению линий ЯМ.Р.

В том случае если частица ц* — электрон (неспаренный спин в парамагнитных веществах), напряженности локальных полей могут достигать 1 Т.

Поле, обусловленное объемной магнитной восприимчивостью.

Под влиянием внешнего магнитного поля в исследуемом веществе- создается намагниченность

M_v—%v'H_a, (1-41)

Рис. 1.17. Магнитный мо­мент (х₂ в системе коорди­нат, связанной с магнит­ным моментом (Х|. Ось г на­правлена вдоль поляризую­щего поля Но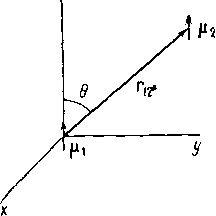

где безразмерный коэффициент %_v называется объемной магнит­ной восприимчивостью. Для диамагнитных вещестз значения %_v отрицательны и для большинства органических молекул состав-

Рис. 1.18. Поле экра­нирования. Электро­ны, расположенные в атоме вокруг ядра, под влиянием поля Но начинают прецес- снровать, создавая поле экранирования

Н Л он

ляют ~10^-6. Поле объемной намагниченности одинаково во всем пространстве исследуемого образца.

Поле электронных токов, индуцированных внешним полем Н₀ (экранирующие поля). В атомах и молекулах под влиянием внеш­него магнитного поля Н₀ возбуждаются электронные токи j (рис. 1.18), создающие собственное поле Н', причем

W-—0- Н₀, (1.42)

где величина о называется постоянной экранирования (как прави­ло, а>0, т. е. поле Н' противоположно по направлению полю Н₀). Химически неэквивалентные позиции ядер в молекуле приводят к различиям в константах экранирования этих ядер. Разность кон­стант экранирования двух ядер a_t и сгг (ai—02) называют химиче­ским сдвигом.

Величины 0 безразмерны и, как правило, приводятся в мил­лионных долях (м. д.), поскольку эффект экранирования в целом иевелик. Абсолютное экранирование существенно зависит от внут­ренних электронов атома или молекулы, однако изменение экрани­рования от молекулы к молекуле (иначе говоря, диапазон химиче-

ских сдвигов) в основном определяется внешними валентными электронами. Эмпирически удалось показать, что диапазон экрани­рования А зависит от заряда атома Z, причем для атомов одного периода системы элементов эта зависимость описывается уравне­нием» А со Z³.

Так, для протонов диапазон сдвигов составляет ~10 м. д.,. ядер ⁾³С— ~300 м. д., ядер ¹⁹F— ~ 1000 м. д.

Различие в константах экранирования приводит к различию соответствующих резонансных частот, поскольку

VA= % H_q-(1—<Ja), vb= # tf₀-(l —cr_B),

где 0а и 0в — константы экранирования ядер А и В, a va и vb — соответствующие резонансные частоты.

Таким образом, спектры ЯМ.Р характеризуются тонкой структу­рой, обусловленной химическими сдвигами.

Косвенное спин-спиновое взаимодействие ядерных моментов. В молекулах невязких жидкостей, несмотря на полное усреднение диполь-дипольного взаимодейст­вия, ядерные спины продолжают взаимодействовать, используя элек­троны связи в качестве своеобраз­ной «линии передачи» спиновой ин­формации. Хотя механизм этого взаимодействия довольно сложен и требует квантовомеханического под­хода, возможна следующая качест­венная интерпретация.

%„S,)

S.

Рис. 1.19. Два магнитных момен» та ядра Ц| и ц₂, входящие в мо­лекулу АВ, взаимно поляризу­ются за счет электронных спинов.

Si и S₂

В случае двухатомной молеку^: лы (два ядра (ii и ц₂ ^и Д^ва элект­рона Si и S₂ (рис. 1.19)) можно по­лагать, что один из электронов Si преимущественно находится у од­ного ядра jiii, а другой электрон S2 — у второго ядра Ц2- Первое ядро Ц1 будет создавать на элект­роне S[ магнитное поле Н(ц_ь Si), напряженность которого пропор­циональна величине магнитного момента ядра ц_ь При этом одна из возможных ориентаций электронного спина (допустим, антипараллельная ориентации первого ядерного спина) окажется более предпочтительной (рис. 1.19). Эта избыточная поляризация спина Si будет пропорциональна величине поля Н(ц1, Si), т. е. величине ц,₄. Поскольку S₂ антипараллелен спину Si согласно прин­ципу Паули, то второй спин также окажется поляризованным отно-

•■•сительно fii. Поляризованный спин S₂ создает на магнитном момен­те ц₂ поле H(S₂, цг), причем напряженность этого поля также про­порциональна fii. Энергия взаимодействия момента fi₂ с полем H(S₂, ц₂) определяется из соотношения

Е = [i₂ ■ Н (S₂, [1₂) = ₂ ■ [Ail

где константа А учитывает «химическую» специфику электронов связи. Обычно энергия косвенного спин-спинового взаимодействия записывается в форме произведения векторов-спинов

E=h-J-(1.43)

где константа / называется константой спин-спинового взаимодей­ствия. Константа / имеет размерность Гц.

Из предложенной картины ясно, что косвенное спин-спиновое взаимодействие осуществляется и в отсутствие внешнего поляри­зующего поля #₀.

Спин-спиновое взаимодействие приводит к появлению дополни­тельной мультиплетной структуры спектров. Если в отсутствие -косвенного взаимодействия ядро А дает резонанс на частоте va, то при «включении» этого взаимодействия половина спинов |л_А испы­тывает воздействие дополнительного поля ядер В, ориентирован­ных параллельно ца, а другая половина — ядер В, ориентирован ных антипараллельно |л_А. Таким образом, в спектре для ядра А сбудут наблюдаться две линии Vi и v₂ с частотами

, 1 1 v_x = \л 4-

2 1 ,

v₂ = v^ -J.

Эти линии образуют дублет с константой / (Гц). Аналогичное расщепление должно соблюдаться и для ядра В.