1. Смеси вещества. Количественный анализ

Типичные примеры смесей компонент: а) растворитель и раство­ренное вещество, б) смесь изомеров, в) смесь оптических изоме­ров, г) смесь изотопомеров, д) реакционная смесь.

Во всех указанных случаях спектр ЯМР будет представлять собой почти линейную суперпозицию спектров отдельных компо­нент. При известных ограничениях (гл. 1) интегральные* интен­сивности, взятые для каждой из компонент, пропорциональны кон­центрациям компонент. Таким образом, можно использовать ин­тегральные интенсивности для проведения количественного анали­за смеси. Важное требование для проведения такого анализа со­стоит в том, чтобы линии спектра ЯМР компонент были смещены друг относительно друга, т. е. компоненты должны быть спект­рально «разрешены». Ограниченная разрешающая способность

спектрометров ЯМР ставит определенные границы в этом отно­шении.

Особо следует остановиться на исследовании оптической чисто­ты органических соединений. Вообще говоря, в ахиральных средах (например, в оптически неактивных растворителях) спектры опти­ческих антиподов не различаются между собой, поэтому исследо­вание оптической чистоты в указанных случаях невозможно. Не­эквивалентность спектров оптических антиподов может возник­нуть только как следствие оптической активности среды. Распро­страненным приемом индуцирования неэквивалентности является введение в раствор обычного ахирального растворителя добавок хиральных сдвигающих реагентов. В качестве такого реагента можно, например, использовать производное европия — трис-(3- трифторометилгидроксиметилен-й-камфорато) -европий.

R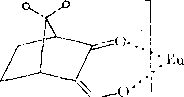

Заметим, что применение шифт-реагента ограничено система­ми, способными к комплексообразованию.

2. Индивидуальные жесткие вещества

Вообще говоря, примеры .жестких органических систем не так многочисленны, как это может показаться с первого взгляда. К числу жестких ^молекул относятся бензол, нафталин, циклопро­пан, норборнан.’норборнен, галоид- и циан-производные этих мо­лекул и ряд других систем. Большинство же органических молекул по существу являются псевдожесткими, поскольку в них имеются определенные возможности для вращений, инверсий, перегруппи­ровок и т. д.

Основная задача, которая выдвигается в отношении жестких молекул, состоит в установлении структуры соединения. В связи с тем что спектральные параметры не имеют ясной и однозначной связи с пространственной структурой молекулы (гл. 3), обычно под установлением структуры понимают выбор одной из доста­точно сильно различающихся структурных гипотез. Так, напри­мер, задачу формулируют как исследование цис- и транс-изоме­рии олефиновых производных, мета-, орто- и пара-изомерных про­изводных замещенных ароматических соединений, типа сочлене­ния циклических систем, 1,1-, 1,2-, 1,3-замещения и т. д. Очень мощным приемом установления структуры является использование элементов симметрии спектра ЯМР, поскольку симметрия спино-

т вой системы, как правило, непосредственно связана с симметри­ей молекулы.

Однако большинство задач исследования жестких молекул формулируются по существу методически (§ 1). При этом не рас­сматривают проблему установления трехмерной пространственной структуры молекулы. В этом случае задачу сводят к расшифровке спектра ЯМР и отнесению спектральных параметров к определен­ным ядрам или парам ядер. Согласно проведенному выше анали­зу полученная при решении такой задачи информация (§ 1) пред­ставляется избыточной в химическом отношении. Более последо­вательная формулировка задач этого типа состоит в том, что не ограничиваются расшифровкой спектра, а пытаются каким-то об­разом интерпретировать полученные значения химических сдви­гов и констант спин-спинового взаимодействия.

Интерпретация спектральных параметров 'требует соответст­вующей теоретической модели. Следует, однако, заметить, что со­временная квантовая химия пока не располагает надежными ме­тодами расчета таких характеристик молекул, как химические сдвиги и константы спин-спинового взаимодействия. По существу все распространенные теоретические модели спектральных пара­метров являются эмпирическими и применимы к очень ограничен­ному кругу объектов. Слабость теоретической платформы подска­зывает следующую стратегию таких исследований: предваритель­но на аналогичных системах развивается локальная модель спект­рального параметра, удовлетворительно работающая на извест­ных примерах, затем эта модель используется при анализе неиз­вестной системы.

3. Динамические молекулы

Понятие «динамическая молекула» может быть использовано в широком и узком смыслах. Динамическими молекулами в широ­ком смысле этого термина называются молекулы, обнаруживаю­щие эффекты химического обмена в спектрах ЯМР в интервале температур 200—400 К. Подобные эффекты наблюдаются в моле­кулярных системах, потенциальные поверхности которых имеют барьеры от 5 до 25 ккал/моль. Экспериментальные данные пока­зывают, что такими свойствами обладают очень многие органиче­ские соединения. Динамическими молекулами в узком смысле на­зываются системы, обнаруживающие эффекты химического обме­на при комнатных температурах. Эти молекулы имеют барьеры от 15 до 18 ккал/моль. Очевидно, что динамичность в узком смыс­ле — сравнительно редкое явление.’

Исследования динамических систем начинают с выбора кине­тической схемы процесса. Кинетическая схема должна учитывать принципиальные особенности процесса: вырождение (обмен меж­ду эквивалентными формами), внутри- или межмолекулярный ха­рактер реакций, эффективный порядок процессов, число форм, участвующих в обмене. Заметим, что кинетическая' схема полно­стью определяет дальнейшую процедуру количественной обработ­ки динамических эффектов. Количественная обработка состоит в определении констант скоростей обмена. В том случае, если иссле­дования проводятся в достаточно широком интервале температур, можно, пользуясь теорией абсолютных скоростей реакций, опре­делить значения активационных параметров процессов AG^ф, АН^ф и А5^ (гл. 4).

4. Псевдожесткие системы

Характерной особенностью псевдожестких систем является нали­чие быстрых (в шкале ЯМР) процессов обмена. Таким образом, как и в случае динамических молекул, исследование псевдожест­ких систем начинают с установления кинетической схемы соеди­нения. Кинетическая схема позволяет определить эффективную симметрию спиновой системы с учетом обмена. Эта эффективная симметрия'‘используется в дальнейшем при расшифровке спект­ров ЯМР.

Принципиальной особенностью спектральных параметров, по­лучаемых в ходе расшифровки спектров псевдожестких систем, является тот факт, что наблюдаемый параметр 0 представляет собой результат усреднения по всем формам соединения

П

е = 5>⁰п (7.9)

/=I

где pi — доля г-той формы; 0_г — значения параметра 0'для г-той формы. Уравнение (7.9) содержит п неизвестных спектральных параметров и (п—1) значений долей форм (сумма долей удовлет-

П

воряет условию ^ p_t — lj. Имеется лишь одна известная ве-

г=1

личина 0. Таким образом, уравнение (7.9) существенно недоопре- делено. В общем случае в результате расшифровки получают на­бор спектральных параметров

П

(7.10)

i=l '

где в,-/ — j-тый спектральный параметр для г-той формы. В этом случае полученная система уравнений оказывается также сущест­венно недоопределенйой.

Для того чтобы уравнение (7.9) или система уравнений (7.10) стали разрешимыми относительно величин p_t и 0_г, необходимо ввести дополнительные условия,

Как уже указывалось, изучение неравновесных систем с помощьк) спектроскопии ЯМР имеет ряд ограничений. Эти ограничения обусловлены тем, что ядерные спины представляют собой доста­точно «инерционную» систему, которая не успевает следить за бы­стрыми химическими процессами. Минимальный период полупре^ вращения вещества ограничен временем спин-решеточной релак­сации Т_и таким образом, быстрые необратимые процессы нельзя изучать с помощью ЯМР. '

Если скорость химического процесса сравнительно мала, то этот процесс может быть изучен как с помощью непрерывного ме­тода, так и с помощью импульсной ЯМР-спектроскопии. В непре­рывном методе минимальное время процесса Г.должно удовлет­ворять условию Г>Г_г, где Т_т — общее время регистрации спект­ра (5—10 мин в стандартных условиях). В импульсной Фурье- спектроскопии это условие может быть несколько ослаблено: Г>- (обычно время Т\ составляет 1-—10 с).