§ 4. Эвристические приемы расшифровки

спектров ЯМР

Расшифровка спектров ЯМР лредставляет собой типичный при­мер решения сложной, но конкретно поставленной задачи. Неко­торые важные принципы расшифровки спектров можно извлечь из анализа общей формальной схемы решения задач. Общая схе­ма решения задач наглядно может быть представлена в виде лабиринта, имеющего вход (эквивалент начальных условий зада­чи) и выход (эквивалент цели задачи). В структуре лабиринта могут быть выделены два принципиально различных элемента — «коридоры» и «развилки». Коридоры представляют собой аналог алгоритмов, т. е. таких стадий решения задачи, которые могут быть реализованы в форме сводки четких правил. Развилки пред­ставляют собой простейший аналог ситуации, связанной с. проб­лемой выбора. Вообще говоря, выбор нужного алгоритма можно проводить случайным образом. Нетрудно, однако, видеть, что при достаточно большом количестве развилок п достижение цели ста­новится затруднительным, если вообще возможным, поскольку количество вариантов прохождения лабиринта быстро растет с увеличением п.

В практической деятельности человек решает проблему вы­бора интуитивно, используя различные эвристические приемы. Строго говоря, эвристические приемы не обеспечивают достиже­ния цели. Однако их можно рассматривать как эмпирические правила, наиболее вероятно применимые в данной ситуации. В основе эвристики лежит метод аналогий и индуктивных выводов.

Таким образом, расшифровку спектров ЯМР можно предста­вить как комплекс алгоритмов и эвристических приемов. Алго­ритмы предпочтительней организовывать на ЭВМ, поскольку ско­рость осуществления арифметических и логических операций у ЭВМ гораздо выше, чем у человека. Кроме того, ЭВМ в боль­шей степени гарантирована от случайных ошибок. Проблема вы­бора алгоритма или, иначе говоря, поиск эвристического приема осуществляется человеком. Некоторые часто встречающиеся на практике эвристические приемы расшифровки спектров обсуж­даются ниже.

1. Использование простейшей интерпретации

Очень часто сигнал или группа сигналов могут быть интерпрети­рованы несколькими способами. Так, два сигнала равной интен­сивности можно рассматривать как дублет с соответствующей константой расщепления и как два синглета с соответствующими химическими сдвигами. Среди всех способов интерпретации сле­дует придерживаться того, который оперирует с минимальным количеством независимых переменных (факторов). Эту интерпре­тацию естественно назвать простейшей. Простейшая интерпрета­ция не всегда оказывается истинной, однако в статистическом смысле (т. е. на большом количестве примеров) указанная стра­тегия приносит успех.

2. Поиск «слабого звена» в задаче

Очень важно в такой громоздкой задаче, которой является анализ спектра, сразу найти часть или подзадачу, допускающую одно­значную интерпретацию. На первых стадиях анализа таким «сла­бым звеном цепи» могут оказаться сигналы стандарта, раствори­теля или каких-то других известных компонент раствора. Кроме гого, простой интерпретации можно ожидать для симметричных ^зких или широких синглетов, не содержащих неразрешенных компонент, простых дублетов, триплетов и других сигналов, уве­ренно обнаруживающихся в спектре. Если удается интерпрети­ровать хотя бы один сигнал, то результаты этой интерпретации :ледует использовать при анализе следующего сигнала и т. д.

3. Поиск кратных отношений и повторяющихся

интервалов

«Избыточная» информация, содержащаяся в спектре, может быть обнаружена в виде различных кратных отношений интеграла, товторяющихся частотных интервалов, центров симметрии мульти- тлетов и т. д. Кратные соотношения для интегральной кривой обычно позволяют выдвинуть гипотезу об индивидуальности со­единения, о числе протонов в отдельных фрагментах' структуры, эб уровнях примесей и т. п. Повторяющиеся интервалы между тиниями являются важным признаком слабосвязанных спиновых систем. Равные расщепления между линиями различных мульти- 1летов, как правило, свидетельствуют о спин-спиновом взаимо­действии между соответствующими протонами. Наличие элемен­тов симметрии в сложном мультиплете в ряде случаев позволяет идентифицировать тип симметрии спиновой системы.

4. Распознавание образов

Зо многих конкретных случаях при анализе сложных спектров шмик использует визуальный подход, основанный на методе рас- гознавания образов. Образом называется такая характеристика объекта, которая несет в себе семантическую (смысловую) инфор­мацию. Распознавание образов спектров ЯМР — наиболее трудно алгоритмизируемая стадия расшифровки.

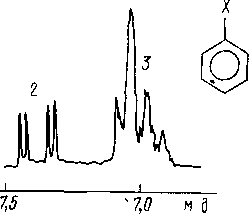
Некоторые фрагменты Молекул имеют достаточно простые ЯМР образы. Так, с помощью спектроЬ ЯМР ‘Н можно легко рас- юзнать этильную группу, изопропильную группу, фенильный ра- шкал, пара-замещенное фенильное ядро, некоторые виды диза- лещенных олефинов и другие (рис. 6.10) .

Псевдопростые спектры. К сожалению, не во всех случаях ме­тод распознавания образов приводит к правильным результатам. Это связано с тем, что один и тот же образ может соответствовать

КСН(СН₃)_г

1 М.0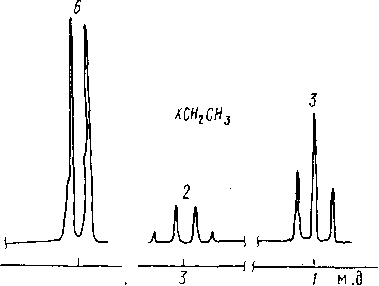

15

7,0 м.Э.

Рис. 6.10. Образы спектров ЯМР 'Н некоторых молекуляр­ных фрагментов. Цифры над группами сигналов соответ­ствуют интегральным интенсивностям этих групп в протон­ных единицах

Н Н \/

/ \ R R

J

5,5

5,0 м .9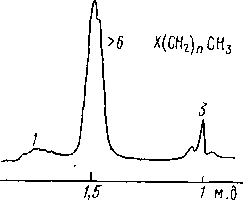

■нескольким типам молекулярных фрагментов. Начинающий химик- органик может допустить следующую довольно распространен­ную ошибку: интерпретировать образ ошибочно, отнеся его к наи­более распространенной структурной ситуации. Спектры, простая интерпретация которых оказывается ложной, называются псевдо-

простыми. Анализ таких спектров в предположении простой ин­терпретации приводит к выявлению так называемых виртуальных констант спин-спинового взаимодействия. Следует отметить, что виртуальная константа не отражает какого-либо физически зна­чимого параметра. -

5. Анализ спектров ЯМР ‘Н при наличии известных структурных параметров

Анализ спектров существенно упрощается, если исследователь располагает какими-то сведениями относительно образца. Ниже рассмотрены некоторые виды предварительной информации и спо­собы ее привлечения при расшифровке спектра.

Соединение индивидуальное. В этом случае следует отыскать кратные соотношения для интегральной кривой. Для молекул с небольшой молекулярной массой можно попытаться определить общее количество протонов (§2).

Общее количество протонов в соединении. Привлечь при ин­терпретации интегральной кривой. Использовать при поиске пред­положительных структурных формул.

Элементный состав. Использовать при поиске предположи­тельной брутто-формулы.

Брутто-формула. Использовать при поиске подходящих струк­турных формул.

Отдельные функциональные группы, «ли фрагменты молекулы. Эти сведения следует использовать при построении структурной модели. Часто удается обнаружить в спектрах сигналы соответст­вующих групп.

Структура с точностью до изомерии. Каждому изомеру соот­ветствует одна или несколько структурных формул. Эти формулы проверяют, используя данные экспериментального спектра..

Структура с точностью до конформаций. Выдвигаются гипоте­тические схемы конформационных превращений, различающихся количеством конформаций и константами равновесий. Эти схемы изучаются с целью проверки их адекватности эксперименту.

Структура соединения, включая конформационный состав. Рас­шифровка спектра сводится к отнесению линий спектра к опре­деленным переходам в соответствующей спиновой диаграмме. Для слабосвязанных систем можно говорить об отнесении групп сиг­налов к определенным ядрам.