4. Системы стабилизации ямр спектрометров

В принципе можно провести эксперимент, при котором в момент прохождения резонансного сигнала /(v) развертка выключается,

Л(|/

№

при этом мы как бы «повисаем» на склоне резонансной линии. Если в дальнейшем ни частота v, ни магнитное поле Н₀ не изме­няются, то уровень сигнала в развертке по времени (рис. 5.6, а) будет оставаться постоянным. Однако реально обе величины (и v, и Н₀) подвержены неста­бильностям, та-к что мы будем наблюдать либо колебания око­ло начального уровня (рис. 5.6, б), либо в случае систематичес­кого дрейфа уход из резонанс­ной области (рис. 5.6, в). Если

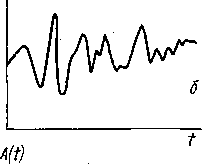
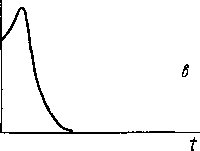
о нестабильностях судить по ре­зультатам этого эксперимента, то очевидно, что невозможно сде­лать вывод о том, какая имен­но из переменных величин (v или ^#₀) нестабильна. Оче-' видно также, что постоянный уровень сигнала (рис. 5.6, а)

Рис. 5.6. Эксперимент ' с «повисанием> на линии ЯМР. Развертка выключена в момент t = t₀. В дальнейшем может на­блюдаться один из трех .случаев: а — стабильное выполнение резонансных ус­ловий; 6 — случайные нестабильности; в — «дрейф» резонансных условий

будет иметь место не только тогда, когда v и Н₀ стабильны, но также если v и Н₀ зависят от времени, но так, что v(t) — fH₀(t).

Эти соображения привели к созданию систем ядерной или спиновой стабилизации, в которых стабилизация осуществляется с помощью самого же сигнала- ЯМР и стабилизируется не каж­дый из параметров v и Н₀, а их отношение v/H₀= ft (рис. 5.7). Нестабильности магнитного поля ±ДН вызывают напряжения разбаланса +V сигнала контрольного, образца, измеряемого в форме сигнала дисперсии. Это напряжение поступает в катушки

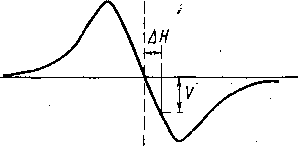
+ Л //компенс

Рис. 5.7. Система спииовой стабилизации

суперстабилизатора отрабатывающей системы с полярностью, при­водящей к компенсации нестабильности АН.

Для того чтобы сделать возможной развертку частоты илн. магнитного поля для регистрации ‘спектра исследуемого образца, каналы стабилизации и регистрации разделяют. Таким образом, в спектрометре фактически воспринимаются два сигнала ЯМР: один из них (контрольный) сначала находят вручную, затем «повисают» на нем п сразу включают систему стабилизации. Пос­ле этого переходят в канал наблюдения и регистрируют изучае­мый спектр. Очевидно, что сигналы контроля и наблюдения долж­ны быть разными. Это требование выполняется одним из двух способов. Во-первых, контрольный сигнал может происходить от образца, непосредственно встроенного в датчик. Такая система называется двухобразцовой (второй образец — сменный, содер­жит изучаемый раствор), а тип контроля — внешним. Во-вторых, стабилизация спектрометра может осуществляться на одном из ■сигналов изучаемого спектра, при этом остальные сигналы запи­сываются с помощью изменения частоты модуляции. Такая систе­ма называется однообразцовой, а тип контроля — внутренним. Разумеется, при использовании однообразцовой стабилизации приходится каждый раз при смене образца производить заново включение контроля.

Практически все современные спектрометры ЯМР располагают возможностью проведения экспериментов по двойному ядерному магнитному резонансу. Этим термином объединяют различные эксперименты, связанные с облучением спиновой системы однов­ременно двумя ВЧ-лолями. Одно из этих полей, имеющее частоту Vi и амплитуду Hi (гл. 1, § 3), называется полем регистрации, поскольку частота vi лежит в диапазоне частот резонанса ядер с гиромагнитным отношением ft i (vi= ft\H₀). Второе ВЧ-поле имеет частоту v₂ и амплитуду Н₂. Оказывается, что при некоторых ус­ловиях спектр, наблюдаемый на частоте vi, зависит от частоты v₂- и амплитуды Я₂. Одно из условий .состоит в том, чтобы частота второго поля находилась в резонансной области других ядер с- гиромагнитным отношением ft ₂(v₂= ft ₂Я₀). В том случае, если ft 1 = ft2, двойной резонанс называют гомоядерным.Так, возможен двойной резонанс типа *Н—{*Н} («протоны наблюдаются, протоны облучаются»), В том случае, если-^1^=-^₂, говорят о гетероядер-

щ
	а
	S
■ |~	^ л

I

ном резонансе. Например, широ­ко применяется двойной резо­нанс ⁶С—{^!Н} («ядра ¹³С на­блюдаются, протоны облучают­ся»).

Виды двойного резонанса.

Классификация методов двойно­го резонанса основывается на способе генерации второй часто­ты гг, способе изменения час­тот vi и v₂ (методе развертки) и величине амплитуды Я₂.

Рис. 5.8. Виды высокочастотного облучения в форме спектральных плотностей У(v): а — когерентное облучение; б — синусоидально-мо- дулированное облучение; в — шу­мовое некогерентное облучение

Тип генерации частоты v₂. Различают следующие случаи:

а) когерентное облучение, б) си­нусоида льно-модулирова"Рнпе об­лучение, в) шумовое облучение. Когерентное облучение осущест­

частота модуляции (рис. 5.8, б). Шумовое облучение осуществля­ется путем случайного (шумового) изменения частоты (чаще фазы) колебаний, что приводит к возбуждению спектра частот, лежащих в диапазоне от v₀—v_m до v₀+v_m (рис. 5.8, в), называе­мого полосой шума.

Следует также различать непрерывный и импульсный методы облучения вторым полем. Импульсный метод широко применяет­ся в Фурье-спектроскопии (гл. 6, § 8).

Виды разверток. Различают три вида разверток: а) частотную, б) полевую, в) по типу ИНДОР. При частотной развертке часто­та V) свипируется, а вторая частота v₂ остается постоянной. При полевой развертке обе частоты свипируются в соответствии с изменениями внешнего магнитного поля -по законам: \’i(0 — = #,Я₀(0 и v₂(t) = % ₂Ho(t) ■ Наконец, в методе ИНДОР частота наблюдения V] удерживается постоянной, а частота v₂ свипиру­ется.

Рис. 5.9. Четырехуровневая диа­грамма системы двух спипов (I— = 1/2) и схема каналов релакса­ции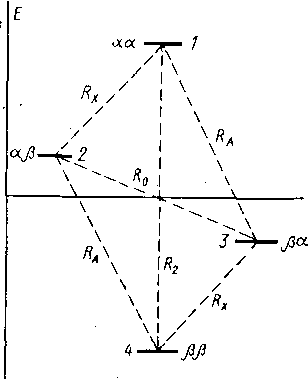

Величина амплитуды уН₂. По величине амплитуды второго поля различают следующие виды двойного резонанса: а) ядер- иый эффект Оверхаузера, б) тик- линг, в) селективный двойной ре­зонанс, г) тотальный двойной резо­нанс.

Ядерный эффект Оверхаузера.

Если частота V2 совпадает с ча­стотой некоторой линии, а ампли­туда уН₂ сравнима по величине с фактором {Т\Т₂)-'1², то эта линяя насыщается. Насыщение одной ли­нии спектра может привести к из­менениям интенсивности других линий спектра, не связанных непо­средственно с облучаемой линией.

Это явление в общем случае назы­вается обобщенным ядерным эф­фектом Оверхаузера.

Различают классический межъ- ядерный эффект Оверхаузера, про­исходящий в системе' спинов, не связанных косвенным спин-спино- вым взаимодействием, и эффект Оверхаузера в связанных спиновых системах (или спектроскопию ИНДОР).

Межъядерный эффект Оверхаузера. Как известно, двухспино­вая система с /ах = 0 (гл. 2, § 1) описывается четырехуровневой спиновой диаграммой (рис. 5.9), где уровни аа, ар, Ра и рр пред­ставлены «чистыми» состояниями. Переходы 2->1 и 4->-3 соответ­ствуют линиям спектра ядра X, а переходы 4^-2 и 3->1 — лини­ям ядра А. Четырехуровневая диаграмма описывается нескольки­

ми релаксационными процессами, характеризующимися скоростя­ми релаксации Ra—l/Ti (ij), где i и / — номера уровней. Соглас­но теории Соломона R_]2 = R₃₄=R_X и R_]3=R_2i=R_A, причем в об­щем случае Ra¥=Rx- Кроме указанных процессов следует рас­смотреть кросс-эффекты, связанные с членами R^=R2 (двухкван­товый переход) и R₂₃=R₀ (нульквантовый переход). В общем случае изменение интенсивности описывается величиной ЯЭО:

9 I,-

;яэо = ^А

;х}

Ri Ro

Yx

Ya

(5.1)

= 1

2R, -j- Ri-j- R₀

где Ya и ух — гиромагнитные отношения для ядер А и X, 1_А — {X} и 1_А — интенсивности линий ядра А три облучении X и без облучения соответственно.

Если диполь-дипольный механизм релаксации является доми­нирующим, то, согласно Соломону, R₂: R_A: Ro= 1:1/4: 1/6, и урав­нение (5.1) упрощается:

(5.2

ЯЭО = 1 4- — (Yx/Ya)-

В частности, при двойном резонансе ¹³С—{⁴Н} (Х=^!Н, А = = ¹³С) ЯЭО составляет примерно 3,0. Это позволяет существенно улучшить отношение сигнал/шум в спектрах ЯМР ¹³С.

ИНДОР-спектроскопия. В связанной спиновой системе типа АХ при /ах^О частоты всех четырех переходов различаются и, следовательно, можно локально насытить только один переход. Так, если облучается переход 4-v3 (рис. 5.9), то изменяются на­селенности уровней 3 и 4 и, следовательно, будут изменяться ин­тенсивности переходов З-vl и 4-v2, имеющих общие уровни с переходом 4-v3. Переход 4-v2, совпадающий с переходом 4-v3 по величинам l_z начального и конечного состояний, называ­ется регрессивным (или Л=0-переходом). Переход З-vl, име­ющий только один уровень с тем же значением /_г, называется прогрессивным (или Л=2-переходом).

В стационарных условиях до насыщения линии 4-v3 населен­ности уровней определяются распределением Больцмана (гл. 1, §2):

N i ~ ехр [— (—m_Ay_AH₀—m_xy_xH₀)!kT], (5.3)

(5.4а) . (5.46)

•(-

⁽⁵'^4в)

что дает для четырех уровней следующие значения: Naa = N1/2,1/2 = ехр

Мхр = /V 1/2, -1/2 = ехр ^

ЛГра = N—1/2,1/2 = ехр

' T ^T* I ' ^H’^,kT

(5.4r)

Npp = —i/г —1/2 =i exp

Введем обозначения: ехр(¹/₂улНоtkT) = 1+Aa и exp (V2YxH₀jkT) — = 1+Ax. Таким образом, для избыточной населенности имеем следующие выражения:

ДЛ^оа = Ал Ах, (5.5а)

*ЛМ*_р = Дл-Лх, (5.56)

A Nfia ~ — Ал f- Ах> (5.5в)

АЛ'рр = — Ад — А_х. (5.5г)

Видно, что населенности уровней несколько различаются между собой, причем в случае гомоядерной системы (у_н—\х) избытки населенности составляют: AN_aa-~2A\ AN^ =—2A; AN_af?,— AN$_a= О

Насыщение одного из переходов вызывает выравнивание насе­ленностей этих уровней. Так, облучая переход 4->3 ((3p-v(3a), вы­равнивают населенности уровней 4 и 3. Новые значения избыточ­ных населенностей будут определяться формулами

ANaa = А_а\--'А_х, (5.6а)

ДЛ^ар = Дл— Ах, (5.66)

A iVpa = АЛ/'рр = (A iVpa ! A TVpp) = —Ад. (5.6в)

Новые населенности оказывают влияние на интенсивности других переходов. До облучения перехода 4-v3 интенсивности линий были пропорциональны разности в избыточных населенностях:

14_з = k (A Nfra — А N рр) — 2k Ах, (5.7а)

l4-*2 ⁼ k{A Not$ — A iVpp) = 2k Ал, (5.76)

1з_,’=/г(АМ*а —ANpa) = 2/г Ал, (5.7в)

1^, = k (A Naa - A Nad) = 2k Ах. (5.7г)

После облучения перехода 4-v3 интенсивности остальных ли­ний будут определяться соотношениями

I₄_,.2 = k (A A^ap — А /Vрр) = — k (— Ал — Ал "1- Ах) = I4-+2 — kAx,'

(5.8а)

I3+1 = k (A Naa — AN pa) = — k (— Ал — Ал — Ах) = 1з-»1⁵, "t ■ k Ах>

(5.86)

I2—>-1 ⁼ (5.8в)

5. Н. М. Сергеев 129

Таким образом, линия 2->1, «е связанная с переходом 4-*3, оста­ется без изменения, регрессивный переход 4-v2 (Л=0) падает то интенсивности, а прогрессивный З-vl (Л=2) растет. Эффект облучения линии 4-v3 демонстрируется на рис. 5.10.

Изменение интенсивностей линий, наблюдаемое под влиянием второго поля, лежит п основе спектроскопии ИНДОР. При этом

а

(3-1) (4-2) (2-1)-(4-5)

б

с помощью частоты vi находят какую-то" линию в сложном муль­типлете, и «зависают» на этой линии (§ 1.4). После этого вклю­чают развертку второй частоты V2 и, свипируя эту частоту ПО спектру, получают ИНДОР-отк- лики на связанных переходах. Как правило, при этом экспе­риментально трудно наблюдать линии, соседние к облучаемой линии, на-пример входящие в тот же мультиплет.

4—

В

Рис. 5.10. ИНДОР-эксперимент для системы АВ: а — спектр системы АВ;

6 — эффект насыщения крайней пра­вой линии; s — ИНДОР-спектр экви­валентен разности спектров б и а

В многоспиновых системах, характеризующихся развитой мультиплетностыо спектров, вид ИНДОР-отклика зависит от относительных знаков констант спин-спинового взаимодействия. ИНДОР-спектроскопия являет­ся наиболее надежным методом анализа спектров сложных спи­новых систем (подробнее см. гл. 6, § 5).

Тиклинг. Тиклинг линий, спек­тра происходит при значениях

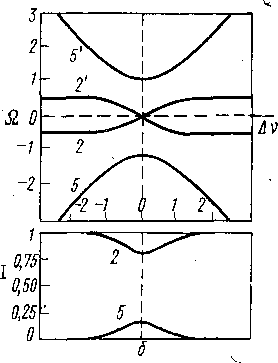
• #₂~Avi/2. Поскольку Avi/2~ ( ^г)^_1/2, тиклинг, как правило, сопровождается эффектом-Оверхаузера. Кроме того, наблюдается дублетное расщепление линий спектра. Точная теория тиклинга требует привлечения довольно громоздкого математического аппа­рата. Качественно картина происходящих изменений описывается с помощью диаграмм Фримена—Андерсона. Эти диаграммы по­казывают изменение частот линий спектра и интенсивностей этих' линий (без учета релаксации) в зависимости от расстройки Av— = vo—V2 и при заданных значениях амплитуды -у Я₂. Для систе­мы АХ диаграммы Фримена—Андерсона для двух случаев ( # #2=0,2/_Ах ^и # #2=/ах) даются на рис. 5.11. Из диаграмм следует, что в случае # #2=0,2 /ах при сильной расстройке |Av|>/ax эффекты двойного резонанса отсутствуют (наблюда­ется дублет линий 2,2' в A-части спектра АХ-системы). При приб­лижении Av к значению частоты одной из линий дублета Х-части при ± //2 возникают боковые компоненты 5 и 5'. При Av=

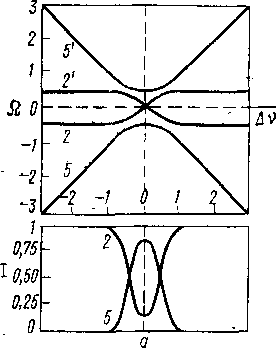_аРис. 5.11. Диаграммы Фримена — Андерсона для системы АХ:

• ft #2=0,2/ах; 6-^ft#₂=-/Ax; Q — частоты сигналов вспек- тре двойного резонанса; зависимости Q от частоты расстройки Av — vx — v₂ приведены на верхних графиках. Интенсивности I сигналов в спектре двойного резонанса приведены на нижн'лх

графиках

111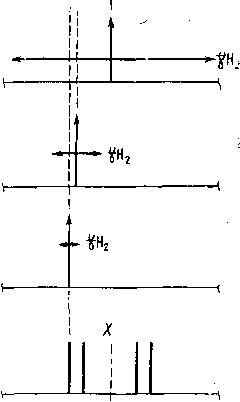

HJ_ II

Рис. 5.12. Эксперименты по двойному резонансу в системе АМХ. а — спектр АМХ; б — тиклинг с облучением крайней левой линии ядра X, видны тиклииг-расщеплеиия линий в А- и М-частях спек­тра; в — селективная развязка, при облучении дублета в спектре ядра X происходит исчезновение расщепления в A-части; г — пол­ная развязка от X, спектр в АМ-части превращается в дублет дуб­летов

= ±7/2 интенсивности всех .компонент, 2,2', 5,5' равны между собой. Этот случай соответствует тиклинг-спектрам.

В сложных спиновых системах 1при облучении какого-то из переходов остальные переходы, связанные с облучаемым по спи­новой диаграмме, испытывают тиклинг-расщепления (рис. 5.12,6). Тиклинг-спектры позволяют также определить относительные зна­ки констант спин-спинового взаимодействия- (гл. 6, § 5).

Селективный двойной резонанс. При дальнейшем повышении до уровня ft происходит явление частичного коллапса

мультиплета. В двухопиновой системе этот эффект может быть получен с помощью диаграмм Фримена—Андерсона. Если ампли­туда ft Н₂ не слишком высока(ft #₂ = /; см., например, рис. 5.11,6), то наряду с центральной линией наблюдаются и боковые, менее интенсивные, компоненты 5,5'. Если же ft Н£^>], то интенсивности утих боковых компонент исчезающе малы, и спектр упрощается до синглета.

Тотальный двойной резонанс. При дальнейшем повыщении %И₂ можно добиться полного коллапса расщеплений, связанных с облучаемым ядром. Так, в трехспиновой системе АМХ при облу­чении с ft Я₂>/ах>^мх обе константы ядра X «исчезают» из спектра, так что спектр в А- и М-частях превращается в дублет дублетов, характерный для двухспиновых систем (рис. 5.12, г).

Тотальный двойной резонанс (или метод спиновой развязки) находит широкое применение в спектроскопии ЯМР. В частности, в ЯМР ⁴Н эта методика часто используется для упрощения спект­ров и для доказательства «спиновой связи» мультшлетов. В спектроскопии ЯМР ¹³С используется полная развязка от всех протонов (ЯМР ¹³С—^Н}). При этом, как травило, применяют шумовую модуляцию частоты второго поля, что позволяет однов­ременно развязываться от всех протонов соединения. Для полной развязки необходимо, чтобы выполнялось условие ft#2>Av, где Av — диапазон химических сдвигов протонов, составляющий при­мерно 1000 Гц. Поскольку требуемая для такого облучения ампли­туда второго ВЧ-поля эквивалентна напряжению на катушке до 10 В, требуется дополнительное охлаждение датчика. В отдель­ных случаях может наблюдаться нагревание образца.