§ 5. Константы /ня

Константы спин-опинового взаимодействия измеряют в Гц. Раз­личают прямые константы /нн (единственная константа такого типа наблюдается в молекуле водорода, см. § 4), геминальные константы ²/нн> вицинальные константы ³/нн и некоторые даль­ние константы ⁴/нн> ⁵/нн (аллильные, гомоаллильные).

1. Закономерности для отдельных типов коистант

Гемииальные константы ²/нн- Эти константы занимают диапазон от —23 Гц (циклопентадиен) до +40 Гц (формальдегид). Неко­торые типичные величины приведены в табл. 3.11. Константы

Типичные значения V_uu в некоторых структурных фрагментах пп

Фрагмент	Примечание	Знак коистаиты	Интервал, Гц
R\ /н R/ хн	линейные цепи	--	10—15
Н\-Хс\	/ п=0 \ П= 1-	—	4— 9 11 — 16
N Н ЮНЛЧ/<н	( /г=0 | «=/ 1 п>2	—	0— 2 6- 9 11—15
с/°Ч/Н 1СНр, н	1 я=0 { «=1 1 *3=2	+	4— 6 6— 7 9—13
*4 /Н
Х = СС^С/(СН2), с	( п>3 t Х = 0, N, S		12—19
м ХНС=С^	—	±	0— 3
— N=cC. к	-—	+	8—16
wy		—	5— 8
чн
Vй
оу ■	—	—	9—13
«ауН*
ДА	/(a, a) /(b, b)	—	8—12 10—14

²/нн могут быть как положительными, так и отрицательными. Эмпирическим путем установлены следующие закономерности.

1. Константа ²/нн растет с увеличением s-характера С Н-свя- зей:

sp³ sp²

метан этилеи

-12,5 +2,5

Согласно квантовохимическим (представлениям связи С—Н в циклопропане имеют (промежуточную гибридизацию (sp^2,s). Кон­станта ²/нн в циклопропане в соответствии с этими представле­ниями равна —4 Гц.

Рис. 3.7. Ориентация я-орбиталн относительно фрагмента СН₂: а — на­правление Н—Н перпендикулярно к плоскости двойной связи; б— на­правление Н—Н параллельно плоскости двойной связи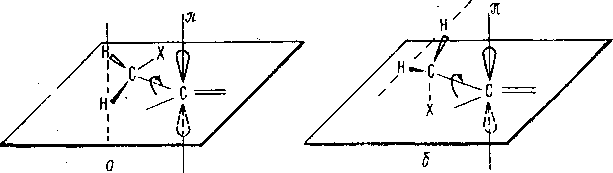

2. Замещение на электроотрицательную группу в ci-положении в СН₂ группе (приводит к росту ²/нн- Например, для,в/?³-гибридн- зации

СН₄ СН₃С1 СН₂С1₂

5. —10,8 —7,5

и для я/7²-гибридизации

формальдегид

+40

этилен

-12,5

3. Замещение на электроотрицательную группу в (3-положении приводит к уменьшению ²/нн- Например:

+2,5

■3,2

-4,8

4

12,5

5. Имеющиеся структурные данные для метиленового фраг­мента СН₂ показывают, что с ростом угла НСН от 107° (цикло гексан) до 115° (циклопропан) константа ²/нн возрастает от —12 до — 4 Гц.

Вицинальные константы ³/нн. Константы ³/_Нн занимают диа­пазон 0-т-20 Гц; они практически всегда положительны. Типичные

. значения констаит ³/нн приведе­ны в табл. 3.12. Установлены следующие закономерности для констант ³/нн.

1. С помощью метода валент­ных структур Карплус показал, что вицинальная константа ³/нн в этаноподобных молекулах за­висит от двугранного угла ср, об­разованного плоскостями НаСаСв и СдСвНв (рис. 3.8). Эта зави­симость, получившая название карплусовской, имеет вид

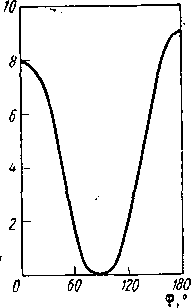
V_Hh = A С oos^a <р (3.26а)

или

Рис. 3.8. Зависимость константы ³/нн зу = Д + В СОв ф } С COS² ф. от двугранного угла фрагмента „ '

Н-С-С-Н (3.266)

Уравнение (3.26 6), содержащее три эмпирических параметра А, В, С, позволяет провести более точную параметризацию. Харак­терной особенностью карплусовской зависимости является су­щественное уменьшение величины констант при значении угла фж90°. Другое важное следствие состоит в различии значений констант при углах ф=0° и ф=180°, что отражается в эмпири­ческих параметрах уравнения (3.266) :А=7, В=—1, С=5 Гц. При этом оказывается, что ³/(ф=0) <³/(ф = 180°).

2. С ростом расстояния в связи С—С константа ³/нн уменьша­ется, что приближенно описывается зависимостью

V_Hh = -35/?cc+ 56, (3.27).

где Rcc — расстояние в связи С—С, А.

3. При прочих равных условиях (двугранный угол ф, длина связи С—С) константа ³/ зависит от электроотрицательности при­соединенных заместителей. Замена водорода на электроотрица­тельный заместитель X в этаноподобных молекулах вызывает уменьшение константы ³/.

Константы ⁴/hhi ⁵/нн- Некоторые примеры констант этого типа приведены в табл. 3.13.

Распространенной структурой, в которой встречается констан­та ⁴/нн, является насыщенная углеродная цепь (рис. 3.9). Кон-

Т а б л и ц а 3.12

Типичные значения V_uu в некоторых структурных фрагментах

ПП

Фрагмент

Примечание

Интервал, Гц,

6— 9

2— 7 5—14

1— 3

G—12 10—19

9—13 G— 8

Н—C-0-C —Н ХСН_а H_b — CHZY H — C-0-C—H ||~||

О о Н —С—с — н

= СН—СН = X

свободное вращение во­круг связи С—С

гош-ориентация СН-свя- зей

граис-ориентация СН- связей

свободное вращение во­круг связи С—С

цис

транс

Х = С Х = 0

7-14

1. 7

2. 4

а—а а—е е—е

Н_а

СН,

цис 1 транс J

2—12

^{сн^О_сщ ^л=2'³

сн

6—12 4— 7

цис

транс

7— 8

орто

п= 1 /г=2 /г=3 п=4

п> 5

1— 2 2— 4 5— 7 8-11 9—13

станта ⁴/нн в этом фрагменте зависит от двугранных углов ф' и ф". В. Ф. Быстров и, А. У. Степанянц показали, что эта зависи­мость имеет вид

(3.28)

⁴/ = Acos² ф'-со5²ф"+С,

где А=0,31 (для ф', ф"<90°), А=3,61 (для ф', ф">90°), А = 1,06

(в остальных случаях); С=—0,35. Как следует из зависимости

f v

/\ <Р'= 180° q>"_ 180"

180'

<Р'“ 180‘ 9'- 90*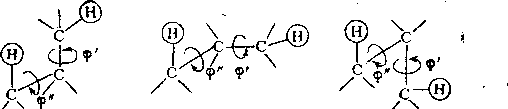

Уин , Г и

т

90⁰

Рис. 3.9. Зависимость константы ⁴/нн в насыщен­ном фрагменте Н—С—С—С—Н от двугранного угла ф' при значениях угла ф", равных 0, 90 н 180°

3

г

о

-/

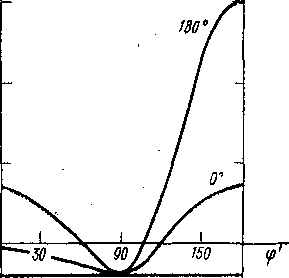
(3.28), 'приведенной на рис. 3.9, константа Чнн достигает 3 Гц при ф"=180° и ф' = 90°. Указанную зависимость ⁴/нн от струк­турных фрагментов иногда выражают как «правило зигзага».

Другой важный тип константы ⁴/нн — так называемые ал- лильные константы (табл. 3.13), которые разделяют на цисоидные и трансоидные. Аллильные константы, как правило, отрицательны и при наличии свободного вращения вокруг связи Сг—Сз имеют величину около —2 Гц, причем обычно ⁴/_транс/<1⁴Лдас. В общем

Фрагмент	Примечание	Интервал, Гц
* X 1 ' о \ о II 0 < • X	г(нс-аллильная т ране-аллильиая	—1,0-—2,2 — 1,4--—2,5
X 1 t 0 1 о II! 0 1 X		—2~—3
7а^^7п
fi /\/1 2 х
с /Г^1 Зх/\ 2 п 5л * Зя ^	JоХ, 51 ^ 1,4 hn, 7и /2п,4 hn. 7н	1,0-1,4 1,7—2,6 1,0 3—4
&	J 2,6 1,3	6,7—8,1 8
' О	мета-4/ пара-5/	1-3 0,2—1,5
X 1 о / о • II о \ о L И4	гомоаллильиая, Ъ1	1—2
	транс, транс-Ч транс, цис-5J	1,3 0,6
И—С —С=С = СН2	Ч	3,3
н
(QIO)	Ч	0,8
н

Некоторые примеры дальних коистант ССВ ⁴/_11Ы н

Нп п п

случае аллильная константа зависит от аллильного угла ф (рис. 3.10). Эта зависимость обнаруживает максимум три ф«90°.

Что касается константы ⁵/нн, то наибольший практический интерес (представляют гомоаллильные константы и константы в

Рис. 3.10. К определению аллильиого угла ф: а — ф = 0°; б — ф = 90°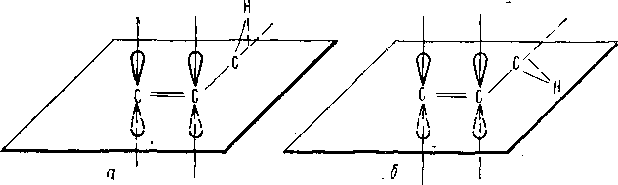

2. сопряженных системах, в частности в ароматических соедине­ниях (табл. 3.13).

   Пример вычисления коистаит спии-спинового взаимодействия J

Как уже указывалось выше (§ 4), применение строгих кваитовохимических методов расчета коистаит спии-спииового взаимодействия до сих пор ограни­чено простейшими молекулами. Полуэмпирические методы (в частности, метод КВ ИНДО) не дают количественного согласия с экспериментом и используют­ся в основном для качественной интерпретации влияния различных структурных факторов. Наиболее эффективные способы предсказания коистаит /нн основы­ваются на использовании спектроструктурных диаграмм и таблиц, модельных соединений, аддитивных схем и т. д.

Таблица 3.14

Константы спнн-спинового взаимодействия в /и/?акогексен-2-але*

Константа	Значения констант, Гц и способ оценки**
	1	2	3	4
’ */44'	—Юн—15	—144—15	— 14,3	_
Уьь-	—10-=—15	—12-.—13	— 12,4
»/„	6—8	7,5—8,0	7,56
3/23	10—19	14,9—16,3	15,6	1
3/34	6-9	6,2—6,6	6,85
	6—9	6,4—7,5	—	6,79
V4 S’	6-9	6,4—7,5	—	6,74
3^86	6—9	6,4—7,5	7,26	—
*J 13	<2	<0,5	— 0,25	—
	Он—2	-1,64—1,7	— 1,65	—
‘/35	<1	<0,5	—1	0,35
	<1	<0,5	—	0,35

* Нумерацию атомов см. на рис. 3.4.

** 1 — спектроспру.ктуриые диаграммы (табл. 3.1.1 —3.13); 2 — таблицы констант см. [4] 3 —модельные соединения; 4_tl’ —пропей [14], ²J₅₅' — метай [15], ‘Jn, ^lJu, —

тране-кротоновый альдегид [16], ³J_SS — пропаи [17]; 4— см. текст.

Рассмотрим в качестве примера оценки коистаит /_Нк в траяс-гексеи-2-але (рис. 3.4). В этом соединении имеется 10 протонов, образующих 6 групп хими­чески эквивалентных ядер. Нетрудно видеть, что протоны групп Н(4) и Н(5) магнитно-неэквивалентны и образуют подсистему АА'ВВ' типа (гл. 2). Таким образом, спектрально значимыми в рассматриваемом случае являются две ге- мииальиыеконстанты 1ц' и /₅₅'шесть вицинальиых констант /i₃, /₂з, /з*. /45, /45’. /_5в и четыре константы через четыре связи /,₃, /24, /35, /46- Кроме того, имеется ряд дальних коистаит (через пять и более связей), но ими можно пренебречь в связи с их малостью.

Использование спектроструктурных корреляций. Самые приближенные оцен­ки коистаит можно провести с помощью даииых, приведенных в табл. 3.11— 3.13. Полученные таким способом значения (табл. 3.14) характеризуются до­вольно значительными разбросами, в отдельных случаях достигающими ±5 Гц. Более точные предсказания можно сделать с помощью справочных даииых Чемберлейна. Эти последние оценки характеризуются ошибками, не превышаю­щими 1 Гц.

Метод модельных соединений. В некоторых случаях удается подыскать соединение, являющееся изоструктурным исследуемому в отношении путн пе­редачи спии-сгшиового взаимодействия между рассматриваемыми ядрами. Ис­пользование подобных модельных структур позволяет получить весьма точные оценки для коистаит спин-спииового взаимодействия. Так, в случае транс-тек- сеи-2-аля константы ⁴/,₃, ³/₂з, ⁴J-u ■ и ³/₃₄ моделируются с помощью транс- кротоиового альдегида. Константы V44,', ²/₅₅' и ³/пб можно оценить с помощью даииых для метана, пропеиа н пропана соответственно (табл. 3.11).

Использование эмпирических корреляций. Более точные оценки дальних констант Ч35 и */*₆ можно получить, например, с помощью эмпирического урав­нения Быстрова — Степаияиц (3.28), используя усреднение коистаит по всем возможным поворотным изомерам, характеризующимся определенными двугран­ными углами ф' и ф". Так как вращение вокруг простых С—С-связей предпо­лагается свободным, то каждый из девяти возможных ротамеров с двугранны­ми углами ф'ф,- = (-60° и ср"=6-60° реализуется с одинаковой вероятностью, равной 1/9. Таким образом, имеем

з з

v-ySS ^{Aik cos2 (!} ■ ^б°⁰⁾ ■ ^{к'^й0О)+с ■

г=1 к=1

Используя численные значения коэффициентов и С, получим

= 0,35 Гц. Для оценки коистаит /45 и /45', которые в общем случае ие совпада­ют, воспользуемся формулами усреднения, приведенными для дизамещеииых этапов XCH2CH2Y. Если вслед за Абрагамом и Гатти ввести следующие обо­значения для констант:

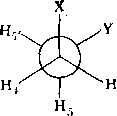
J45 ~ Ртранс-^f Ргош (Jg ^g) >

J 45' ⁼ Ртранс¹^ “Ь 2p_rom/g-

Если предположить, что вращение вокруг связи С—С свободно, то очевидно, ЧТО Ртранс = Ргош= 1/3. Оценки коистаит /<*, J_t*, /**, /_е*' и /*⁽ проводятся с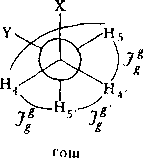

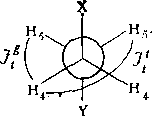
то получим

помощью двух модельных соединений: 2, 2, 5, 5-тетраметилгексаиа [18] и цик- •логексаиа ,[19]. Первая модель дает значения коистаит /('=4,3 и /(‘=12,94 Гц. Вторая модель позволяет оценить значения коистаит в гош-ротамере: /*‘ = = 13,12, /** = 3,65 и Jg¹' — 2,96 Гц. Используя эти значения в формулах усред­нения, получим /₄₅= 6,79 Гц; /«'==6,74 Гц.

Таким образом, система АА'ВВ', образуемая магиитио-иеэквивалеитиыми протонами 4, 4', 5, 5', в данном случае практически вырождается до системы AiB₂, так как ожидаемые значения коистаит /45 и /45' различаются всего лишь на 0,05 Гц. Это соображение может оказаться чрезвычайно полезным при экс­периментальной расшифровке спектра транс-гексеи-2-аля.