Расчет ошибок с сау при случайных воздействиях

Рассмотрим порядок расчета ошибок в системах управления при случайных воздействиях. Пусть задана система, приведенная на рис.11.3.3

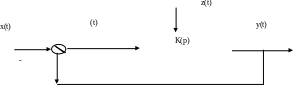
Рис.11.3.3

Необходимо определить величину средней квадратичной ошибки - если заданы Sxx() и Szz().

Рассмотрим несколько случаев.

Пусть действует только полезный сигнал x(t) а помеха z(t) отсутствует.

Спектральная плотность ошибки определяется соотношением:

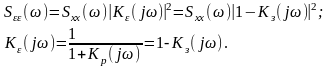(11.3.8)

Величина средней квадратичной ошибки - определяется по формуле:

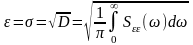. (11.3.9)

Значения интеграла от спектральной плотности табулированы и могут быть вычислены через коэффициенты полиномов выражения для спектральной плотности.

Пусть действует только помеха z(t) а полезный сигнал x(t) отсутствует.

Действие помехи рассматривается на выходе системы.

Спектральная плотность ошибки при этом определяется соотношением:

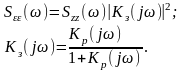(11.3.10)

3. Пусть действует и полезный сигнал x(t) и помеха z(t) и они не коррелированны.

Суммарная спектральная плотность ошибки при этом определяется соотношением:

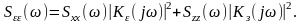(11.3.11)

Пример 11.3.2. Для приведенной ниже системы (рис.11.3.4), определить величину средней квадратичной ошибки -, если заданы Sxx() = c2 и Szz() = 0.

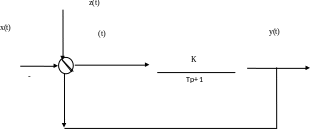
Рис. 11.3.4

Если сигнал и помеха некоррелированны, то суммарная спектральная плотность ошибки при этом определяется соотношением: .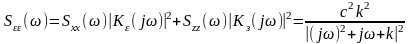

Значения интеграла от спектральной плотности вычислим через коэффициенты полиномов выражения для спектральной плотности.

Величина средней квадратичной ошибки - определяется по формуле:

.

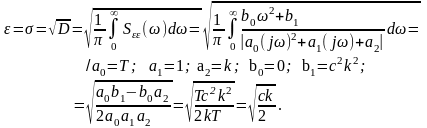Пример 11.3.3. Для системы приведенной на рис.3 определить спектральную плотность ошибки, вызванную действием помехи -z(t) со спектральной плотностью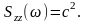

Р

y

ис. 11.3.5

Решение: Спектральная плотность ошибки определяется из соотношений: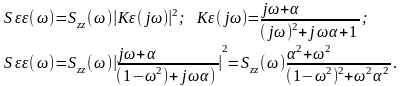

Вычисление и минимизация дисперсии сигнала ошибки замкнутой системы

Обобщенная алгоритмическая схема которой показана на рис. 11.3.5, а.

Будем считать, что передаточная функция W (р), равная произведению передаточных функций объекта и управляющего устройства, известна. Не заданы могут быть лишь некоторые параметры управляющего устройства.

На систему действуют случайные возмущения х_п и х_в с известными спектральными плотностями и . Задающее воздействие также является случайным сигналом со спектральной плотностью .Пусть все три воздействия — центрированные сигналы. Тогда и сигнал ошибки будет центрированным.

Если указанные внешние воздействия не коррелированы между собой, то сигнал ошибки , возникающий в системе, может рассматриваться как сумма трех независимых составляющих (рис. 11.3.5, б):

(11.3.12)

Составляющая обусловлена неточным воспроизведением задающего воздействия, а составляющие и — неполным подавлением возмущений х_п и х_в.

Соответственно и дисперсия сигнала ошибки может быть представлена в виде суммы трех дисперсий:

(11.3.13)

Каждая из этих дисперсий может быть вычислена по формуле (11.2.17) независимо друг от друга:

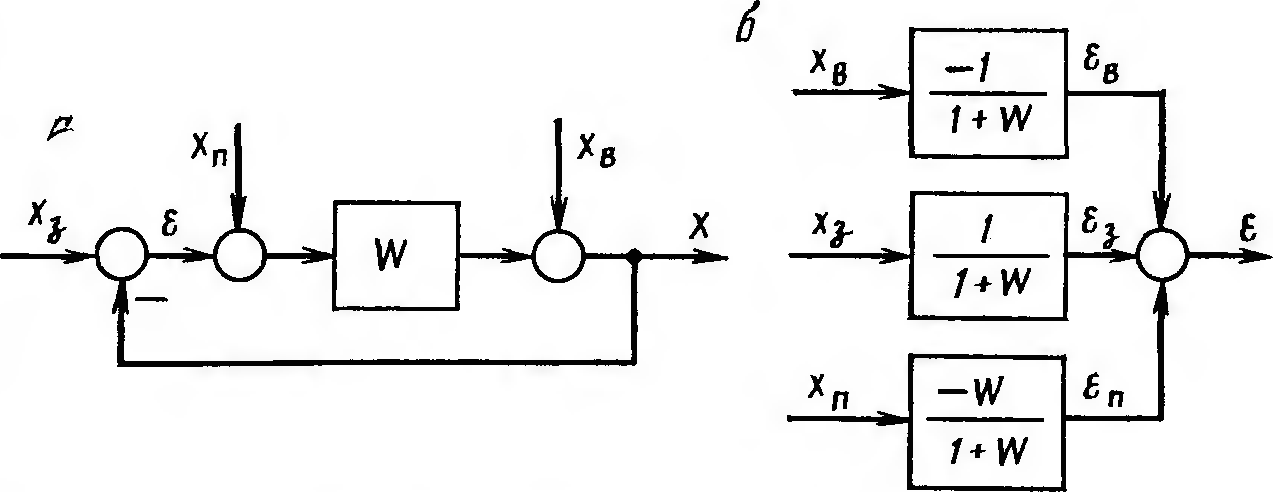Рис. 11.3.5

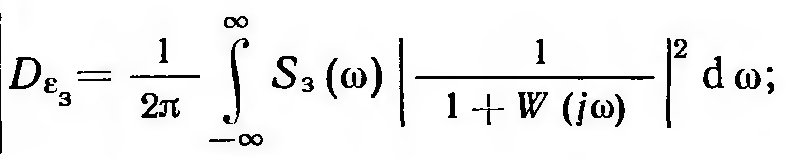(11.3.14)

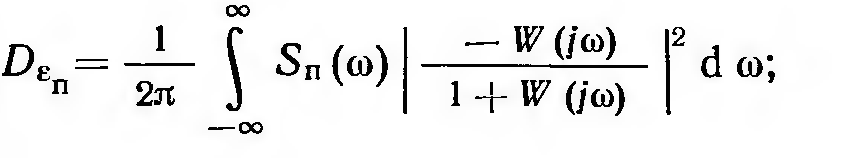(11.3.15)

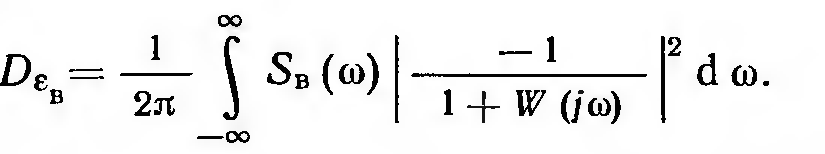(11.3.16)

Если внешние воздействия коррелированы между собой, то и составляющие (11.3.12) сигнала ошибки будут коррелированы, поэтому полную дисперсию можно вычислить только путем интегрирования общей спектральной плотности , найденной с учетом свойства (11.1.30).

При подстановке в формулы (11.2.28) — (11.2.30) конкретных функций и получаются довольно сложные выражения, интегрирование которых обычными методами затруднительно. Поэтому используют методику для вычисления квадратичных интегральных оценок. В соответствии с этой методикой каждую из трех дисперсий определяют по формуле:

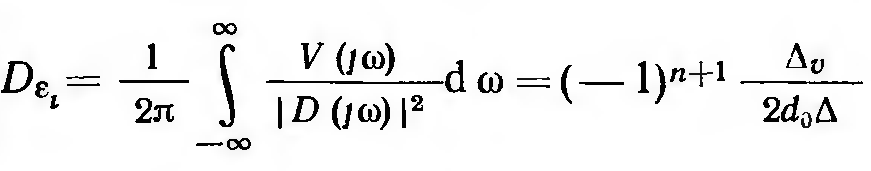(11.3.17)

где полиномы , и определители и составляются по формулам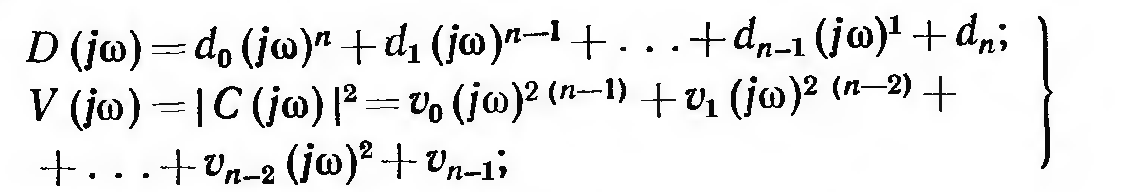 и

.

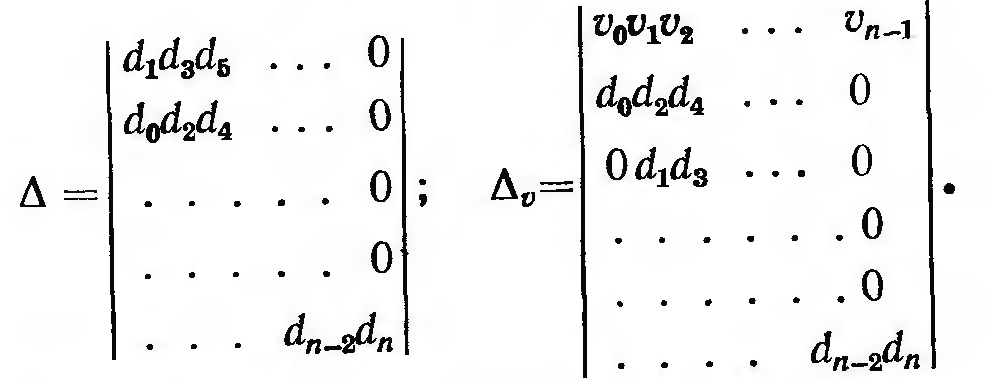В простейших случаях, когда наибольшая степень полинома , формула (11.3.17) будет иметь вид:

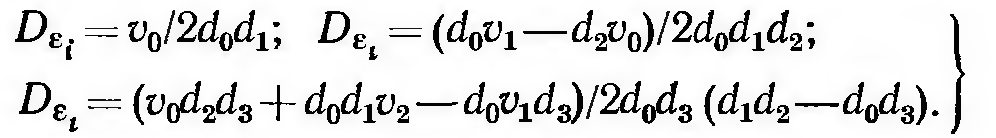(11.3.18)

В полином в виде сомножителя входит характеристическая функция замкнутой системы. Поэтому при приближении системы к границе устойчивости [при ] интеграл (11.3.17) резко возрастает.

Для систем с запаздыванием подынтегральное выражение нельзя привести к виду (11.3.17) и дисперсию можно вычислить только приближенно, заменяя запаздывание дробно-рациональной функцией.

С помощью формул (11.3.13) — (11.3.18) можно получить аналитическое выражение, связывающее полную дисперсию сигнала ошибки с параметрами внешних воздействий и с параметрами системы (например, ):

. (11.3.19)

Минимизируя функцию (11.3.19) по параметрам и можно определить их оптимальные значения.

Покажем, что минимум функции (11.3.19), как правило, существует. Пусть на систему действуют задающее воздействие и помеха х_п. Как правило, спектр задающего воздействия находится в области низких частот (рис. 11.3.6, а), а спектр помехи равномерен

Рис 11.3.6 Влияние передаточного коэффициента разомкнутого контура на спектральную плотность сигнала ошибки

Рис. 11.3.7. График зависимости дисперсии сигнала ошибки от передаточного коэффициента разомкнутого контура

в широкой полосе частот (рис. 11.3.6, в). С увеличением передаточного коэффициента k разомкнутого контура а. ч. х. и по каналам и смещаются в область более высоких частот, а резонансный пик становится выше (см. рис. 11.3.6, а, в, пунктирные кривые).

Так как спектральные плотности равны произведениям и на соответствующие а. ч. х. замкнутой системы, то при увеличении k ординаты функции уменьшаются (рис. 11.3.6, б), а ординаты функции увеличиваются (рис. 11.3.6, г). Соответственно меняются и составляющие полной дисперсии: уменьшается при увеличении k, a — увеличивается (рис. 11.3.7). Очевидно, что суммарная дисперсия при некотором значении k = k_oпm будет иметь минимум.